Non-Euclidean Gradient Descent Operates at the Edge of Stability

The Edge of Stability (EoS) is a phenomenon where the sharpness (largest eigenvalue) of the Hessian converges to $2/η$ during training with gradient descent (GD) with a step-size $η$. Despite (apparently) violating classical smoothness assumptions, EoS has been widely observed in deep learning, but its theoretical foundations remain incomplete. We provide an interpretation of EoS through the lens of Directional Smoothness Mishkin et al. [2024]. This interpretation naturally extends to non-Euclidean norms, which we use to define generalized sharpness under an arbitrary norm. Our generalized sharpness measure includes previously studied vanilla GD and preconditioned GD as special cases, as well as methods for which EoS has not been studied, such as $\ell_{\infty}$-descent, Block CD, Spectral GD, and Muon without momentum. Through experiments on neural networks, we show that non-Euclidean GD with our generalized sharpness also exhibits progressive sharpening followed by oscillations around or above the threshold $2/η$. Practically, our framework provides a single, geometry-aware spectral measure that works across optimizers.

Tight Bounds for Logistic Regression with Large Stepsize Gradient Descent in Low Dimension

We consider the optimization problem of minimizing the logistic loss with gradient descent to train a linear model for binary classification with separable data. With a budget of $T$ iterations, it was recently shown that an accelerated $1/T^2$ rate is possible by choosing a large step size $η= Θ(γ^2 T)$ (where $γ$ is the dataset's margin) despite the resulting non-monotonicity of the loss. In this paper, we provide a tighter analysis of gradient descent for this problem when the data is two-dimensional: we show that GD with a sufficiently large learning rate $η$ finds a point with loss smaller than $\mathcal{O}(1/(ηT))$, as long as $T \geq Ω(n/γ+ 1/γ^2)$, where $n$ is the dataset size. Our improved rate comes from a tighter bound on the time $τ$ that it takes for GD to transition from unstable (non-monotonic loss) to stable (monotonic loss), via a fine-grained analysis of the oscillatory dynamics of GD in the subspace orthogonal to the max-margin classifier. We also provide a lower bound of $τ$ matching our upper bound up to logarithmic factors, showing that our analysis is tight.

Complexity Lower Bounds of Adaptive Gradient Algorithms for Non-convex Stochastic Optimization under Relaxed Smoothness

Recent results in non-convex stochastic optimization demonstrate the convergence of popular adaptive algorithms (e.g., AdaGrad) under the $(L_0, L_1)$-smoothness condition, but the rate of convergence is a higher-order polynomial in terms of problem parameters like the smoothness constants. The complexity guaranteed by such algorithms to find an $\epsilon$-stationary point may be significantly larger than the optimal complexity of $\Theta \left( \Delta L \sigma^2 \epsilon^{-4} \right)$ achieved by SGD in the $L$-smooth setting, where $\Delta$ is the initial optimality gap, $\sigma^2$ is the variance of stochastic gradient. However, it is currently not known whether these higher-order dependencies can be tightened. To answer this question, we investigate complexity lower bounds for several adaptive optimization algorithms in the $(L_0, L_1)$-smooth setting, with a focus on the dependence in terms of problem parameters $\Delta, L_0, L_1$. We provide complexity bounds for three variations of AdaGrad, which show at least a quadratic dependence on problem parameters $\Delta, L_0, L_1$. Notably, we show that the decorrelated variant of AdaGrad-Norm requires at least $\Omega \left( \Delta^2 L_1^2 \sigma^2 \epsilon^{-4} \right)$ stochastic gradient queries to find an $\epsilon$-stationary point. We also provide a lower bound for SGD with a broad class of adaptive stepsizes. Our results show that, for certain adaptive algorithms, the $(L_0, L_1)$-smooth setting is fundamentally more difficult than the standard smooth setting, in terms of the initial optimality gap and the smoothness constants.

Local Steps Speed Up Local GD for Heterogeneous Distributed Logistic Regression

We analyze two variants of Local Gradient Descent applied to distributed logistic regression with heterogeneous, separable data and show convergence at the rate $O(1/KR)$ for $K$ local steps and sufficiently large $R$ communication rounds. In contrast, all existing convergence guarantees for Local GD applied to any problem are at least $\Omega(1/R)$, meaning they fail to show the benefit of local updates. The key to our improved guarantee is showing progress on the logistic regression objective when using a large stepsize $\eta \gg 1/K$, whereas prior analysis depends on $\eta \leq 1/K$.

Federated Learning under Periodic Client Participation and Heterogeneous Data: A New Communication-Efficient Algorithm and Analysis

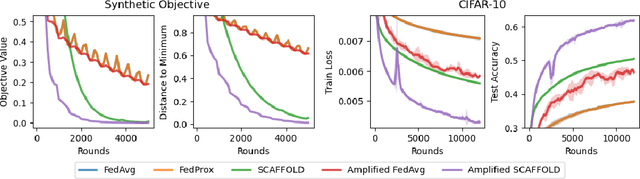
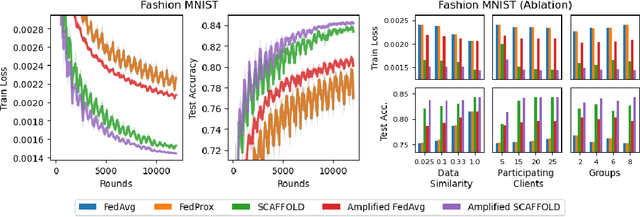
In federated learning, it is common to assume that clients are always available to participate in training, which may not be feasible with user devices in practice. Recent works analyze federated learning under more realistic participation patterns, such as cyclic client availability or arbitrary participation. However, all such works either require strong assumptions (e.g., all clients participate almost surely within a bounded window), do not achieve linear speedup and reduced communication rounds, or are not applicable in the general non-convex setting. In this work, we focus on nonconvex optimization and consider participation patterns in which the chance of participation over a fixed window of rounds is equal among all clients, which includes cyclic client availability as a special case. Under this setting, we propose a new algorithm, named Amplified SCAFFOLD, and prove that it achieves linear speedup, reduced communication, and resilience to data heterogeneity simultaneously. In particular, for cyclic participation, our algorithm is proved to enjoy $\mathcal{O}(\epsilon^{-2})$ communication rounds to find an $\epsilon$-stationary point in the non-convex stochastic setting. In contrast, the prior work under the same setting requires $\mathcal{O}(\kappa^2 \epsilon^{-4})$ communication rounds, where $\kappa$ denotes the data heterogeneity. Therefore, our algorithm significantly reduces communication rounds due to better dependency in terms of $\epsilon$ and $\kappa$. Our analysis relies on a fine-grained treatment of the nested dependence between client participation and errors in the control variates, which results in tighter guarantees than previous work. We also provide experimental results with (1) synthetic data and (2) real-world data with a large number of clients $(N = 250)$, demonstrating the effectiveness of our algorithm under periodic client participation.

EPISODE: Episodic Gradient Clipping with Periodic Resampled Corrections for Federated Learning with Heterogeneous Data

Gradient clipping is an important technique for deep neural networks with exploding gradients, such as recurrent neural networks. Recent studies have shown that the loss functions of these networks do not satisfy the conventional smoothness condition, but instead satisfy a relaxed smoothness condition, i.e., the Lipschitz constant of the gradient scales linearly in terms of the gradient norm. Due to this observation, several gradient clipping algorithms have been developed for nonconvex and relaxed-smooth functions. However, the existing algorithms only apply to the single-machine or multiple-machine setting with homogeneous data across machines. It remains unclear how to design provably efficient gradient clipping algorithms in the general Federated Learning (FL) setting with heterogeneous data and limited communication rounds. In this paper, we design EPISODE, the very first algorithm to solve FL problems with heterogeneous data in the nonconvex and relaxed smoothness setting. The key ingredients of the algorithm are two new techniques called \textit{episodic gradient clipping} and \textit{periodic resampled corrections}. At the beginning of each round, EPISODE resamples stochastic gradients from each client and obtains the global averaged gradient, which is used to (1) determine whether to apply gradient clipping for the entire round and (2) construct local gradient corrections for each client. Notably, our algorithm and analysis provide a unified framework for both homogeneous and heterogeneous data under any noise level of the stochastic gradient, and it achieves state-of-the-art complexity results. In particular, we prove that EPISODE can achieve linear speedup in the number of machines, and it requires significantly fewer communication rounds. Experiments on several heterogeneous datasets show the superior performance of EPISODE over several strong baselines in FL.

Robustness to Unbounded Smoothness of Generalized SignSGD

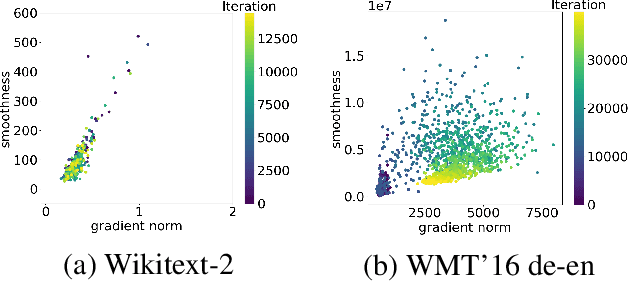
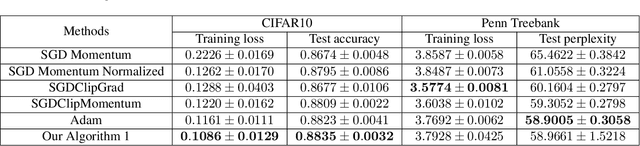
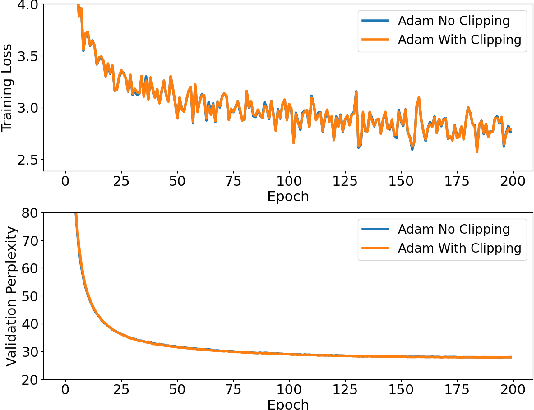
Traditional analyses in non-convex optimization typically rely on the smoothness assumption, namely requiring the gradients to be Lipschitz. However, recent evidence shows that this smoothness condition does not capture the properties of some deep learning objective functions, including the ones involving Recurrent Neural Networks and LSTMs. Instead, they satisfy a much more relaxed condition, with potentially unbounded smoothness. Under this relaxed assumption, it has been theoretically and empirically shown that the gradient-clipped SGD has an advantage over the vanilla one. In this paper, we show that clipping is not indispensable for Adam-type algorithms in tackling such scenarios: we theoretically prove that a generalized SignSGD algorithm can obtain similar convergence rates as SGD with clipping but does not need explicit clipping at all. This family of algorithms on one end recovers SignSGD and on the other end closely resembles the popular Adam algorithm. Our analysis underlines the critical role that momentum plays in analyzing SignSGD-type and Adam-type algorithms: it not only reduces the effects of noise, thus removing the need for large mini-batch in previous analyses of SignSGD-type algorithms, but it also substantially reduces the effects of unbounded smoothness and gradient norms. We also compare these algorithms with popular optimizers on a set of deep learning tasks, observing that we can match the performance of Adam while beating the others.

Fast Composite Optimization and Statistical Recovery in Federated Learning

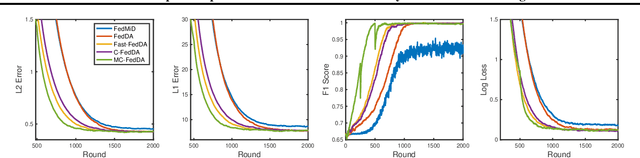
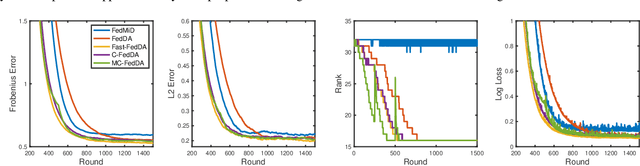
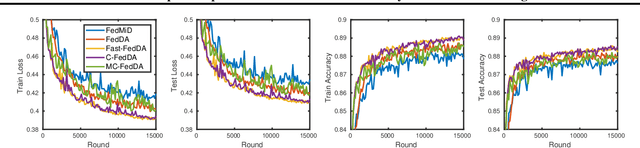
As a prevalent distributed learning paradigm, Federated Learning (FL) trains a global model on a massive amount of devices with infrequent communication. This paper investigates a class of composite optimization and statistical recovery problems in the FL setting, whose loss function consists of a data-dependent smooth loss and a non-smooth regularizer. Examples include sparse linear regression using Lasso, low-rank matrix recovery using nuclear norm regularization, etc. In the existing literature, federated composite optimization algorithms are designed only from an optimization perspective without any statistical guarantees. In addition, they do not consider commonly used (restricted) strong convexity in statistical recovery problems. We advance the frontiers of this problem from both optimization and statistical perspectives. From optimization upfront, we propose a new algorithm named \textit{Fast Federated Dual Averaging} for strongly convex and smooth loss and establish state-of-the-art iteration and communication complexity in the composite setting. In particular, we prove that it enjoys a fast rate, linear speedup, and reduced communication rounds. From statistical upfront, for restricted strongly convex and smooth loss, we design another algorithm, namely \textit{Multi-stage Federated Dual Averaging}, and prove a high probability complexity bound with linear speedup up to optimal statistical precision. Experiments in both synthetic and real data demonstrate that our methods perform better than other baselines. To the best of our knowledge, this is the first work providing fast optimization algorithms and statistical recovery guarantees for composite problems in FL.

SLAW: Scaled Loss Approximate Weighting for Efficient Multi-Task Learning

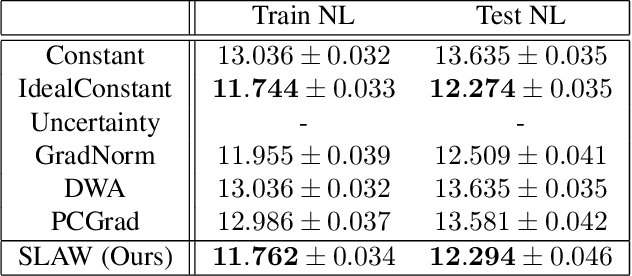
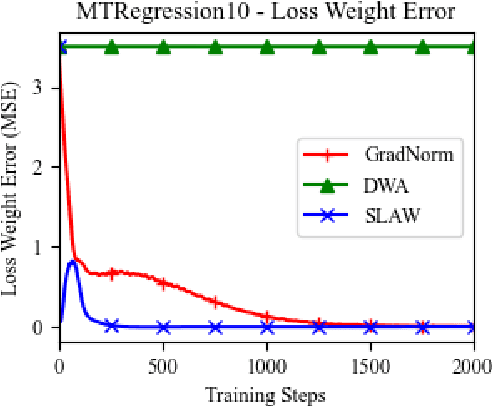
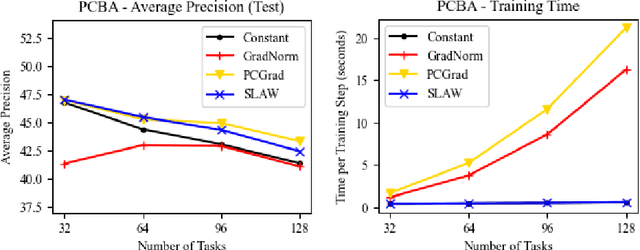
Multi-task learning (MTL) is a subfield of machine learning with important applications, but the multi-objective nature of optimization in MTL leads to difficulties in balancing training between tasks. The best MTL optimization methods require individually computing the gradient of each task's loss function, which impedes scalability to a large number of tasks. In this paper, we propose Scaled Loss Approximate Weighting (SLAW), a method for multi-task optimization that matches the performance of the best existing methods while being much more efficient. SLAW balances learning between tasks by estimating the magnitudes of each task's gradient without performing any extra backward passes. We provide theoretical and empirical justification for SLAW's estimation of gradient magnitudes. Experimental results on non-linear regression, multi-task computer vision, and virtual screening for drug discovery demonstrate that SLAW is significantly more efficient than strong baselines without sacrificing performance and applicable to a diverse range of domains.

Multi-Task Learning with Deep Neural Networks: A Survey

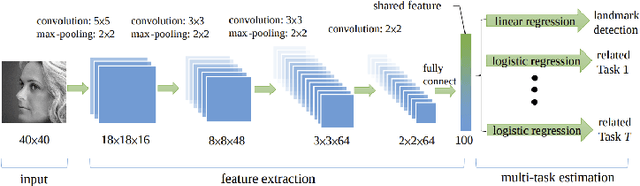
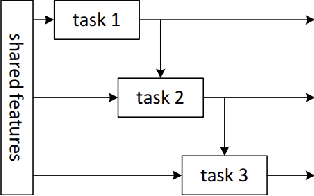
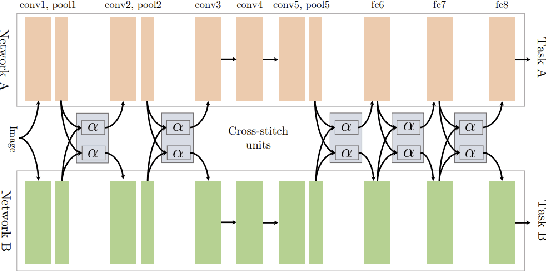
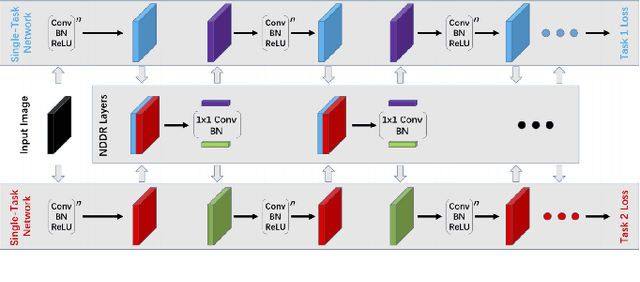
Multi-task learning (MTL) is a subfield of machine learning in which multiple tasks are simultaneously learned by a shared model. Such approaches offer advantages like improved data efficiency, reduced overfitting through shared representations, and fast learning by leveraging auxiliary information. However, the simultaneous learning of multiple tasks presents new design and optimization challenges, and choosing which tasks should be learned jointly is in itself a non-trivial problem. In this survey, we give an overview of multi-task learning methods for deep neural networks, with the aim of summarizing both the well-established and most recent directions within the field. Our discussion is structured according to a partition of the existing deep MTL techniques into three groups: architectures, optimization methods, and task relationship learning. We also provide a summary of common multi-task benchmarks.