SGSR: Structure-Guided Multi-Contrast MRI Super-Resolution via Spatio-Frequency Co-Query Attention

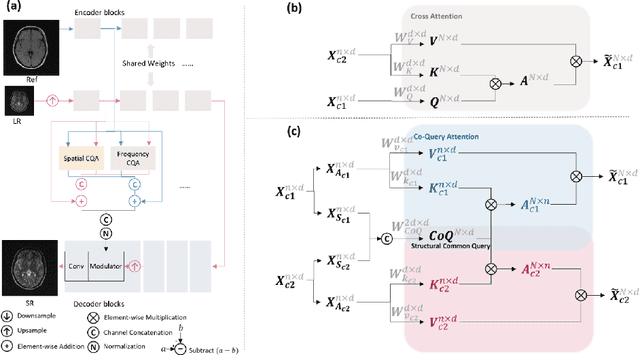
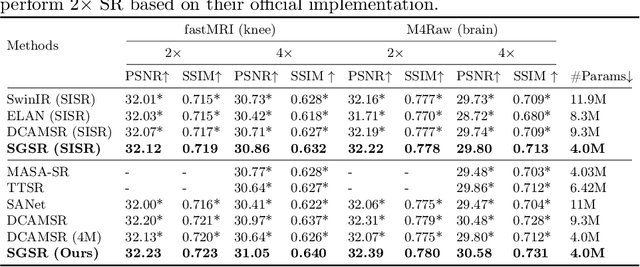
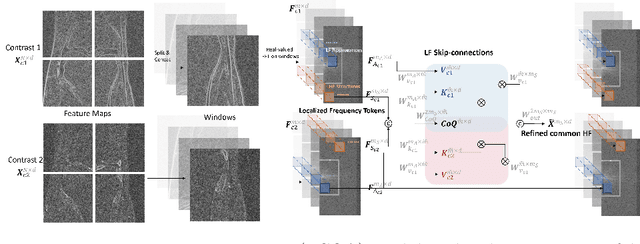
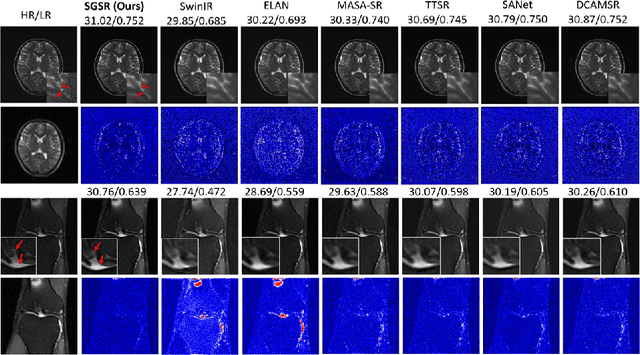
Magnetic Resonance Imaging (MRI) is a leading diagnostic modality for a wide range of exams, where multiple contrast images are often acquired for characterizing different tissues. However, acquiring high-resolution MRI typically extends scan time, which can introduce motion artifacts. Super-resolution of MRI therefore emerges as a promising approach to mitigate these challenges. Earlier studies have investigated the use of multiple contrasts for MRI super-resolution (MCSR), whereas majority of them did not fully exploit the rich contrast-invariant structural information. To fully utilize such crucial prior knowledge of multi-contrast MRI, in this work, we propose a novel structure-guided MCSR (SGSR) framework based on a new spatio-frequency co-query attention (CQA) mechanism. Specifically, CQA performs attention on features of multiple contrasts with a shared structural query, which is particularly designed to extract, fuse, and refine the common structures from different contrasts. We further propose a novel frequency-domain CQA module in addition to the spatial domain, to enable more fine-grained structural refinement. Extensive experiments on fastMRI knee data and low-field brain MRI show that SGSR outperforms state-of-the-art MCSR methods with statistical significance.

CAR: Contrast-Agnostic Deformable Medical Image Registration with Contrast-Invariant Latent Regularization

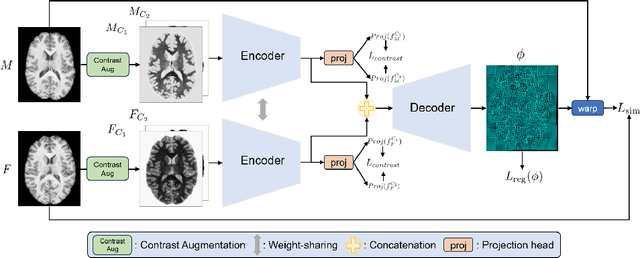
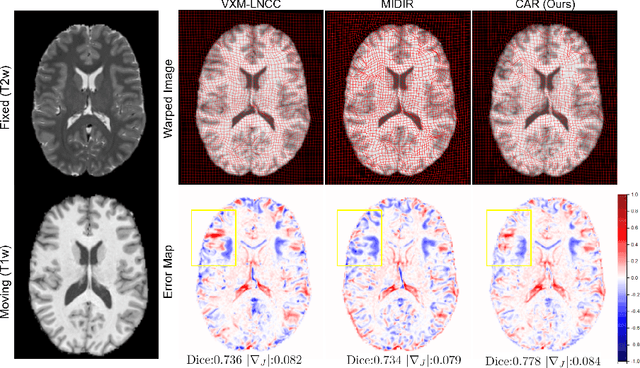
Multi-contrast image registration is a challenging task due to the complex intensity relationships between different imaging contrasts. Conventional image registration methods are typically based on iterative optimizations for each input image pair, which is time-consuming and sensitive to contrast variations. While learning-based approaches are much faster during the inference stage, due to generalizability issues, they typically can only be applied to the fixed contrasts observed during the training stage. In this work, we propose a novel contrast-agnostic deformable image registration framework that can be generalized to arbitrary contrast images, without observing them during training. Particularly, we propose a random convolution-based contrast augmentation scheme, which simulates arbitrary contrasts of images over a single image contrast while preserving their inherent structural information. To ensure that the network can learn contrast-invariant representations for facilitating contrast-agnostic registration, we further introduce contrast-invariant latent regularization (CLR) that regularizes representation in latent space through a contrast invariance loss. Experiments show that CAR outperforms the baseline approaches regarding registration accuracy and also possesses better generalization ability to unseen imaging contrasts. Code is available at \url{https://github.com/Yinsong0510/CAR}.

TIP: Tabular-Image Pre-training for Multimodal Classification with Incomplete Data

Images and structured tables are essential parts of real-world databases. Though tabular-image representation learning is promising to create new insights, it remains a challenging task, as tabular data is typically heterogeneous and incomplete, presenting significant modality disparities with images. Earlier works have mainly focused on simple modality fusion strategies in complete data scenarios, without considering the missing data issue, and thus are limited in practice. In this paper, we propose TIP, a novel tabular-image pre-training framework for learning multimodal representations robust to incomplete tabular data. Specifically, TIP investigates a novel self-supervised learning (SSL) strategy, including a masked tabular reconstruction task for tackling data missingness, and image-tabular matching and contrastive learning objectives to capture multimodal information. Moreover, TIP proposes a versatile tabular encoder tailored for incomplete, heterogeneous tabular data and a multimodal interaction module for inter-modality representation learning. Experiments are performed on downstream multimodal classification tasks using both natural and medical image datasets. The results show that TIP outperforms state-of-the-art supervised/SSL image/multimodal algorithms in both complete and incomplete data scenarios. Our code is available at https://github.com/siyi-wind/TIP.

Tracking Dynamic Gaussian Density with a Theoretically Optimal Sliding Window Approach

Dynamic density estimation is ubiquitous in many applications, including computer vision and signal processing. One popular method to tackle this problem is the "sliding window" kernel density estimator. There exist various implementations of this method that use heuristically defined weight sequences for the observed data. The weight sequence, however, is a key aspect of the estimator affecting the tracking performance significantly. In this work, we study the exact mean integrated squared error (MISE) of "sliding window" Gaussian Kernel Density Estimators for evolving Gaussian densities. We provide a principled guide for choosing the optimal weight sequence by theoretically characterizing the exact MISE, which can be formulated as constrained quadratic programming. We present empirical evidence with synthetic datasets to show that our weighting scheme indeed improves the tracking performance compared to heuristic approaches.

Conditional Deformable Image Registration with Spatially-Variant and Adaptive Regularization

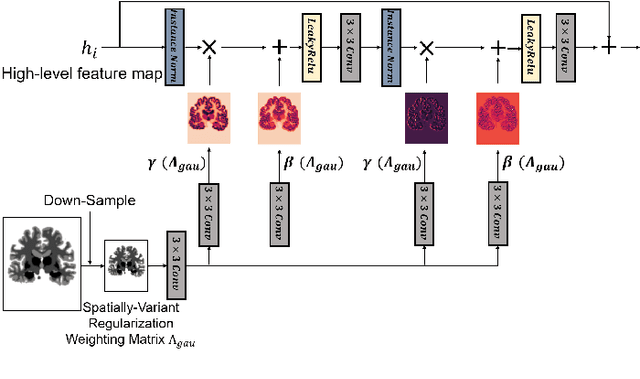
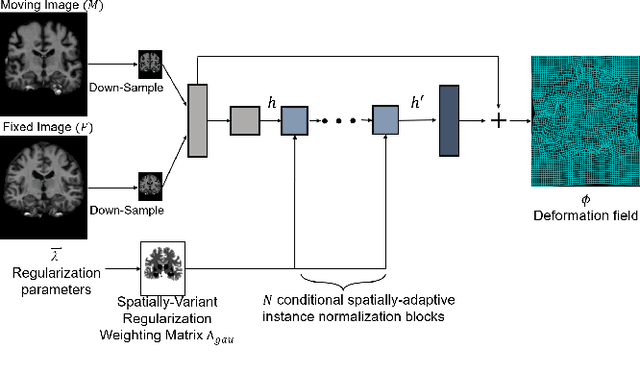
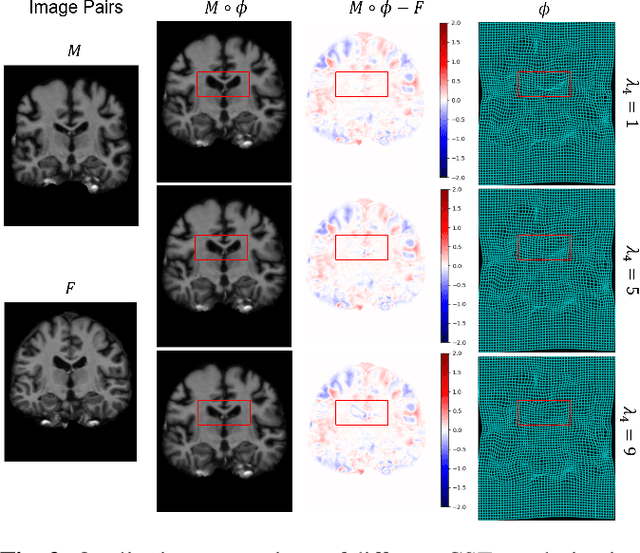
Deep learning-based image registration approaches have shown competitive performance and run-time advantages compared to conventional image registration methods. However, existing learning-based approaches mostly require to train separate models with respect to different regularization hyperparameters for manual hyperparameter searching and often do not allow spatially-variant regularization. In this work, we propose a learning-based registration approach based on a novel conditional spatially adaptive instance normalization (CSAIN) to address these challenges. The proposed method introduces a spatially-variant regularization and learns its effect of achieving spatially-adaptive regularization by conditioning the registration network on the hyperparameter matrix via CSAIN. This allows varying of spatially adaptive regularization at inference to obtain multiple plausible deformations with a single pre-trained model. Additionally, the proposed method enables automatic hyperparameter optimization to avoid manual hyperparameter searching. Experiments show that our proposed method outperforms the baseline approaches while achieving spatially-variant and adaptive regularization.

TAP: The Attention Patch for Cross-Modal Knowledge Transfer from Unlabeled Data

This work investigates the intersection of cross modal learning and semi supervised learning, where we aim to improve the supervised learning performance of the primary modality by borrowing missing information from an unlabeled modality. We investigate this problem from a Nadaraya Watson (NW) kernel regression perspective and show that this formulation implicitly leads to a kernelized cross attention module. To this end, we propose The Attention Patch (TAP), a simple neural network plugin that allows data level knowledge transfer from the unlabeled modality. We provide numerical simulations on three real world datasets to examine each aspect of TAP and show that a TAP integration in a neural network can improve generalization performance using the unlabeled modality.

TAKDE: Temporal Adaptive Kernel Density Estimator for Real-Time Dynamic Density Estimation

Real-time density estimation is ubiquitous in many applications, including computer vision and signal processing. Kernel density estimation is arguably one of the most commonly used density estimation techniques, and the use of "sliding window" mechanism adapts kernel density estimators to dynamic processes. In this paper, we derive the asymptotic mean integrated squared error (AMISE) upper bound for the "sliding window" kernel density estimator. This upper bound provides a principled guide to devise a novel estimator, which we name the temporal adaptive kernel density estimator (TAKDE). Compared to heuristic approaches for "sliding window" kernel density estimator, TAKDE is theoretically optimal in terms of the worst-case AMISE. We provide numerical experiments using synthetic and real-world datasets, showing that TAKDE outperforms other state-of-the-art dynamic density estimators (including those outside of kernel family). In particular, TAKDE achieves a superior test log-likelihood with a smaller runtime.

Learning from Non-IID Data in Hilbert Spaces: An Optimal Recovery Perspective

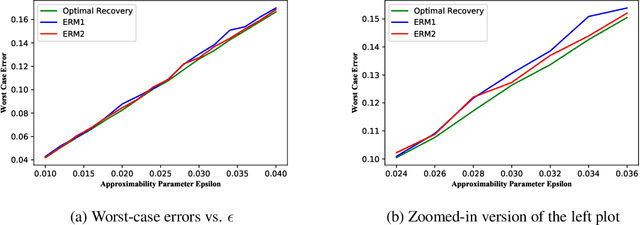
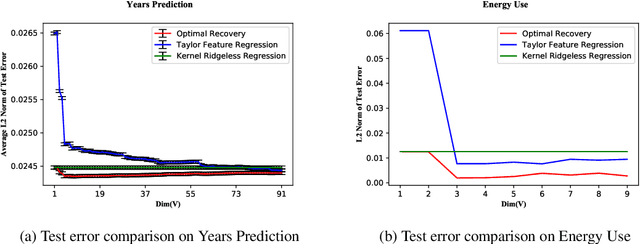
The notion of generalization in classical Statistical Learning is often attached to the postulate that data points are independent and identically distributed (IID) random variables. While relevant in many applications, this postulate may not hold in general, encouraging the development of learning frameworks that are robust to non-IID data. In this work, we consider the regression problem from an Optimal Recovery perspective. Relying on a model assumption comparable to choosing a hypothesis class, a learner aims at minimizing the worst-case (prediction) error, without recourse to IID assumption on data. We first develop a semidefinite program for calculating the worst-case error of any recovery map in finite-dimensional Hilbert spaces. Then, for any Hilbert space, we show that Optimal Recovery provides a formula which is user-friendly from an algorithmic point-of-view, as long as the hypothesis class is linear. Interestingly, this formula coincides with kernel ridgeless regression in some cases, proving that minimizing the average error and worst-case error can yield the same solution. We provide numerical experiments in support of our theoretical findings.

A General Scoring Rule for Randomized Kernel Approximation with Application to Canonical Correlation Analysis

Random features has been widely used for kernel approximation in large-scale machine learning. A number of recent studies have explored data-dependent sampling of features, modifying the stochastic oracle from which random features are sampled. While proposed techniques in this realm improve the approximation, their application is limited to a specific learning task. In this paper, we propose a general scoring rule for sampling random features, which can be employed for various applications with some adjustments. We first observe that our method can recover a number of data-dependent sampling methods (e.g., leverage scores and energy-based sampling). Then, we restrict our attention to a ubiquitous problem in statistics and machine learning, namely Canonical Correlation Analysis (CCA). We provide a principled guide for finding the distribution maximizing the canonical correlations, resulting in a novel data-dependent method for sampling features. Numerical experiments verify that our algorithm consistently outperforms other sampling techniques in the CCA task.

Distributed Parameter Estimation in Randomized One-hidden-layer Neural Networks

This paper addresses distributed parameter estimation in randomized one-hidden-layer neural networks. A group of agents sequentially receive measurements of an unknown parameter that is only partially observable to them. In this paper, we present a fully distributed estimation algorithm where agents exchange local estimates with their neighbors to collectively identify the true value of the parameter. We prove that this distributed update provides an asymptotically unbiased estimator of the unknown parameter, i.e., the first moment of the expected global error converges to zero asymptotically. We further analyze the efficiency of the proposed estimation scheme by establishing an asymptotic upper bound on the variance of the global error. Applying our method to a real-world dataset related to appliances energy prediction, we observe that our empirical findings verify the theoretical results.