Differentially Private Random Feature Model
Paper and Code
Dec 06, 2024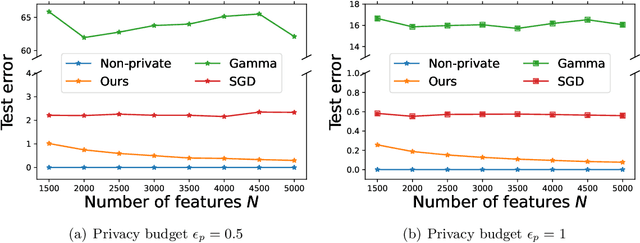
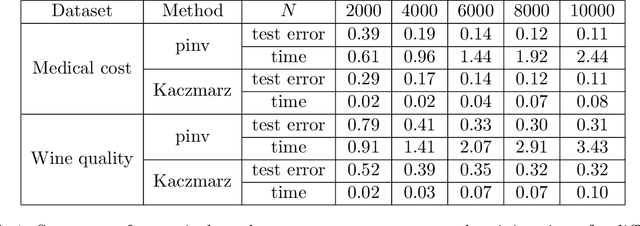
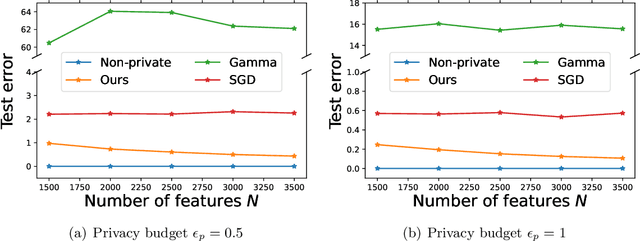
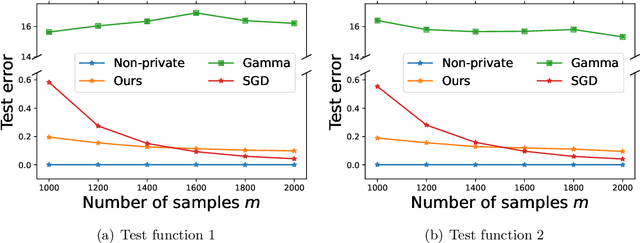
Designing privacy-preserving machine learning algorithms has received great attention in recent years, especially in the setting when the data contains sensitive information. Differential privacy (DP) is a widely used mechanism for data analysis with privacy guarantees. In this paper, we produce a differentially private random feature model. Random features, which were proposed to approximate large-scale kernel machines, have been used to study privacy-preserving kernel machines as well. We consider the over-parametrized regime (more features than samples) where the non-private random feature model is learned via solving the min-norm interpolation problem, and then we apply output perturbation techniques to produce a private model. We show that our method preserves privacy and derive a generalization error bound for the method. To the best of our knowledge, we are the first to consider privacy-preserving random feature models in the over-parametrized regime and provide theoretical guarantees. We empirically compare our method with other privacy-preserving learning methods in the literature as well. Our results show that our approach is superior to the other methods in terms of generalization performance on synthetic data and benchmark data sets. Additionally, it was recently observed that DP mechanisms may exhibit and exacerbate disparate impact, which means that the outcomes of DP learning algorithms vary significantly among different groups. We show that both theoretically and empirically, random features have the potential to reduce disparate impact, and hence achieve better fairness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge