Precision Neural Network Quantization via Learnable Adaptive Modules

Quantization Aware Training (QAT) is a neural network quantization technique that compresses model size and improves operational efficiency while effectively maintaining model performance. The paradigm of QAT is to introduce fake quantization operators during the training process, allowing the model to autonomously compensate for information loss caused by quantization. Making quantization parameters trainable can significantly improve the performance of QAT, but at the cost of compromising the flexibility during inference, especially when dealing with activation values with substantially different distributions. In this paper, we propose an effective learnable adaptive neural network quantization method, called Adaptive Step Size Quantization (ASQ), to resolve this conflict. Specifically, the proposed ASQ method first dynamically adjusts quantization scaling factors through a trained module capable of accommodating different activations. Then, to address the rigid resolution issue inherent in Power of Two (POT) quantization, we propose an efficient non-uniform quantization scheme. We utilize the Power Of Square root of Two (POST) as the basis for exponential quantization, effectively handling the bell-shaped distribution of neural network weights across various bit-widths while maintaining computational efficiency through a Look-Up Table method (LUT). Extensive experimental results demonstrate that the proposed ASQ method is superior to the state-of-the-art QAT approaches. Notably that the ASQ is even competitive compared to full precision baselines, with its 4-bit quantized ResNet34 model improving accuracy by 1.2\% on ImageNet.

Randomized Kaczmarz Methods with Beyond-Krylov Convergence

Randomized Kaczmarz methods form a family of linear system solvers which converge by repeatedly projecting their iterates onto randomly sampled equations. While effective in some contexts, such as highly over-determined least squares, Kaczmarz methods are traditionally deemed secondary to Krylov subspace methods, since this latter family of solvers can exploit outliers in the input's singular value distribution to attain fast convergence on ill-conditioned systems. In this paper, we introduce Kaczmarz++, an accelerated randomized block Kaczmarz algorithm that exploits outlying singular values in the input to attain a fast Krylov-style convergence. Moreover, we show that Kaczmarz++ captures large outlying singular values provably faster than popular Krylov methods, for both over- and under-determined systems. We also develop an optimized variant for positive semidefinite systems, called CD++, demonstrating empirically that it is competitive in arithmetic operations with both CG and GMRES on a collection of benchmark problems. To attain these results, we introduce several novel algorithmic improvements to the Kaczmarz framework, including adaptive momentum acceleration, Tikhonov-regularized projections, and a memoization scheme for reusing information from previously sampled equation~blocks.

Task-Oriented Edge-Assisted Cooperative Data Compression, Communications and Computing for UGV-Enhanced Warehouse Logistics

Only the chairs can edit This paper explores the growing need for task-oriented communications in warehouse logistics, where traditional communication Key Performance Indicators (KPIs)-such as latency, reliability, and throughput-often do not fully meet task requirements. As the complexity of data flow management in large-scale device networks increases, there is also a pressing need for innovative cross-system designs that balance data compression, communication, and computation. To address these challenges, we propose a task-oriented, edge-assisted framework for cooperative data compression, communication, and computing in Unmanned Ground Vehicle (UGV)-enhanced warehouse logistics. In this framework, two UGVs collaborate to transport cargo, with control functions-navigation for the front UGV and following/conveyance for the rear UGV-offloaded to the edge server to accommodate their limited on-board computing resources. We develop a Deep Reinforcement Learning (DRL)-based two-stage point cloud data compression algorithm that dynamically and collaboratively adjusts compression ratios according to task requirements, significantly reducing communication overhead. System-level simulations of our UGV logistics prototype demonstrate the framework's effectiveness and its potential for swift real-world implementation.

Faster Linear Systems and Matrix Norm Approximation via Multi-level Sketched Preconditioning

We present a new class of preconditioned iterative methods for solving linear systems of the form $Ax = b$. Our methods are based on constructing a low-rank Nystr\"om approximation to $A$ using sparse random sketching. This approximation is used to construct a preconditioner, which itself is inverted quickly using additional levels of random sketching and preconditioning. We prove that the convergence of our methods depends on a natural average condition number of $A$, which improves as the rank of the Nystr\"om approximation increases. Concretely, this allows us to obtain faster runtimes for a number of fundamental linear algebraic problems: 1. We show how to solve any $n\times n$ linear system that is well-conditioned except for $k$ outlying large singular values in $\tilde{O}(n^{2.065} + k^\omega)$ time, improving on a recent result of [Derezi\'nski, Yang, STOC 2024] for all $k \gtrsim n^{0.78}$. 2. We give the first $\tilde{O}(n^2 + {d_\lambda}^{\omega}$) time algorithm for solving a regularized linear system $(A + \lambda I)x = b$, where $A$ is positive semidefinite with effective dimension $d_\lambda$. This problem arises in applications like Gaussian process regression. 3. We give faster algorithms for approximating Schatten $p$-norms and other matrix norms. For example, for the Schatten 1 (nuclear) norm, we give an algorithm that runs in $\tilde{O}(n^{2.11})$ time, improving on an $\tilde{O}(n^{2.18})$ method of [Musco et al., ITCS 2018]. Interestingly, previous state-of-the-art algorithms for most of the problems above relied on stochastic iterative methods, like stochastic coordinate and gradient descent. Our work takes a completely different approach, instead leveraging tools from matrix sketching.

HERTA: A High-Efficiency and Rigorous Training Algorithm for Unfolded Graph Neural Networks

As a variant of Graph Neural Networks (GNNs), Unfolded GNNs offer enhanced interpretability and flexibility over traditional designs. Nevertheless, they still suffer from scalability challenges when it comes to the training cost. Although many methods have been proposed to address the scalability issues, they mostly focus on per-iteration efficiency, without worst-case convergence guarantees. Moreover, those methods typically add components to or modify the original model, thus possibly breaking the interpretability of Unfolded GNNs. In this paper, we propose HERTA: a High-Efficiency and Rigorous Training Algorithm for Unfolded GNNs that accelerates the whole training process, achieving a nearly-linear time worst-case training guarantee. Crucially, HERTA converges to the optimum of the original model, thus preserving the interpretability of Unfolded GNNs. Additionally, as a byproduct of HERTA, we propose a new spectral sparsification method applicable to normalized and regularized graph Laplacians that ensures tighter bounds for our algorithm than existing spectral sparsifiers do. Experiments on real-world datasets verify the superiority of HERTA as well as its adaptability to various loss functions and optimizers.

Solving Dense Linear Systems Faster than via Preconditioning

We give a stochastic optimization algorithm that solves a dense $n\times n$ real-valued linear system $Ax=b$, returning $\tilde x$ such that $\|A\tilde x-b\|\leq \epsilon\|b\|$ in time: $$\tilde O((n^2+nk^{\omega-1})\log1/\epsilon),$$ where $k$ is the number of singular values of $A$ larger than $O(1)$ times its smallest positive singular value, $\omega < 2.372$ is the matrix multiplication exponent, and $\tilde O$ hides a poly-logarithmic in $n$ factor. When $k=O(n^{1-\theta})$ (namely, $A$ has a flat-tailed spectrum, e.g., due to noisy data or regularization), this improves on both the cost of solving the system directly, as well as on the cost of preconditioning an iterative method such as conjugate gradient. In particular, our algorithm has an $\tilde O(n^2)$ runtime when $k=O(n^{0.729})$. We further adapt this result to sparse positive semidefinite matrices and least squares regression. Our main algorithm can be viewed as a randomized block coordinate descent method, where the key challenge is simultaneously ensuring good convergence and fast per-iteration time. In our analysis, we use theory of majorization for elementary symmetric polynomials to establish a sharp convergence guarantee when coordinate blocks are sampled using a determinantal point process. We then use a Markov chain coupling argument to show that similar convergence can be attained with a cheaper sampling scheme, and accelerate the block coordinate descent update via matrix sketching.

CharacterGLM: Customizing Chinese Conversational AI Characters with Large Language Models

In this paper, we present CharacterGLM, a series of models built upon ChatGLM, with model sizes ranging from 6B to 66B parameters. Our CharacterGLM is designed for generating Character-based Dialogues (CharacterDial), which aims to equip a conversational AI system with character customization for satisfying people's inherent social desires and emotional needs. On top of CharacterGLM, we can customize various AI characters or social agents by configuring their attributes (identities, interests, viewpoints, experiences, achievements, social relationships, etc.) and behaviors (linguistic features, emotional expressions, interaction patterns, etc.). Our model outperforms most mainstream close-source large langauge models, including the GPT series, especially in terms of consistency, human-likeness, and engagement according to manual evaluations. We will release our 6B version of CharacterGLM and a subset of training data to facilitate further research development in the direction of character-based dialogue generation.

Federated Adversarial Learning: A Framework with Convergence Analysis

Federated learning (FL) is a trending training paradigm to utilize decentralized training data. FL allows clients to update model parameters locally for several epochs, then share them to a global model for aggregation. This training paradigm with multi-local step updating before aggregation exposes unique vulnerabilities to adversarial attacks. Adversarial training is a popular and effective method to improve the robustness of networks against adversaries. In this work, we formulate a general form of federated adversarial learning (FAL) that is adapted from adversarial learning in the centralized setting. On the client side of FL training, FAL has an inner loop to generate adversarial samples for adversarial training and an outer loop to update local model parameters. On the server side, FAL aggregates local model updates and broadcast the aggregated model. We design a global robust training loss and formulate FAL training as a min-max optimization problem. Unlike the convergence analysis in classical centralized training that relies on the gradient direction, it is significantly harder to analyze the convergence in FAL for three reasons: 1) the complexity of min-max optimization, 2) model not updating in the gradient direction due to the multi-local updates on the client-side before aggregation and 3) inter-client heterogeneity. We address these challenges by using appropriate gradient approximation and coupling techniques and present the convergence analysis in the over-parameterized regime. Our main result theoretically shows that the minimum loss under our algorithm can converge to $\epsilon$ small with chosen learning rate and communication rounds. It is noteworthy that our analysis is feasible for non-IID clients.

Pixelated Butterfly: Simple and Efficient Sparse training for Neural Network Models

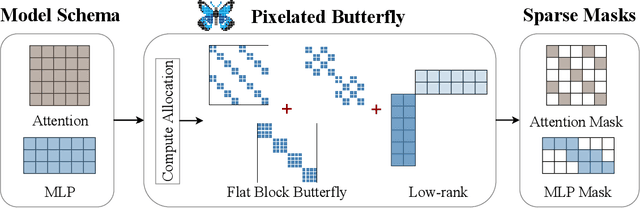
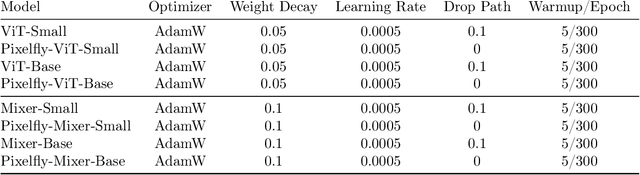
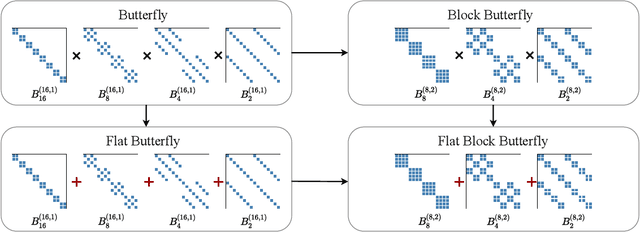
Overparameterized neural networks generalize well but are expensive to train. Ideally, one would like to reduce their computational cost while retaining their generalization benefits. Sparse model training is a simple and promising approach to achieve this, but there remain challenges as existing methods struggle with accuracy loss, slow training runtime, or difficulty in sparsifying all model components. The core problem is that searching for a sparsity mask over a discrete set of sparse matrices is difficult and expensive. To address this, our main insight is to optimize over a continuous superset of sparse matrices with a fixed structure known as products of butterfly matrices. As butterfly matrices are not hardware efficient, we propose simple variants of butterfly (block and flat) to take advantage of modern hardware. Our method (Pixelated Butterfly) uses a simple fixed sparsity pattern based on flat block butterfly and low-rank matrices to sparsify most network layers (e.g., attention, MLP). We empirically validate that Pixelated Butterfly is 3x faster than butterfly and speeds up training to achieve favorable accuracy--efficiency tradeoffs. On the ImageNet classification and WikiText-103 language modeling tasks, our sparse models train up to 2.5x faster than the dense MLP-Mixer, Vision Transformer, and GPT-2 medium with no drop in accuracy.