Kernel Alignment for Unsupervised Feature Selection via Matrix Factorization
Paper and Code
Mar 13, 2024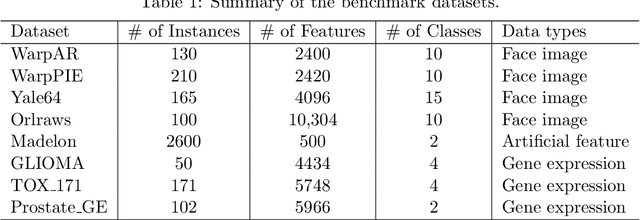
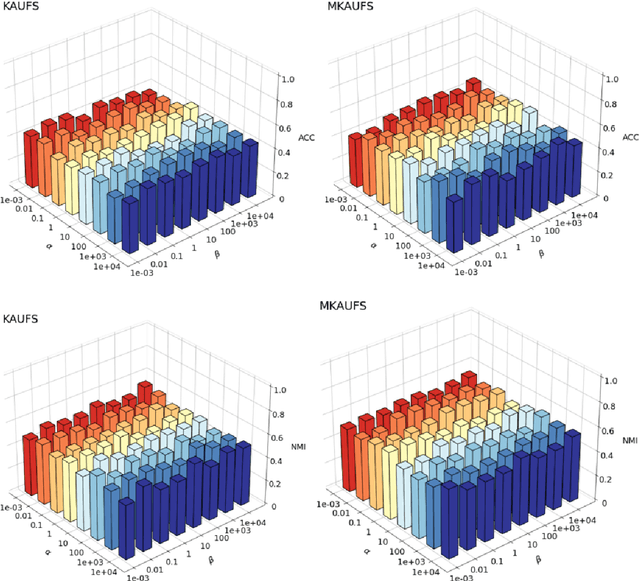
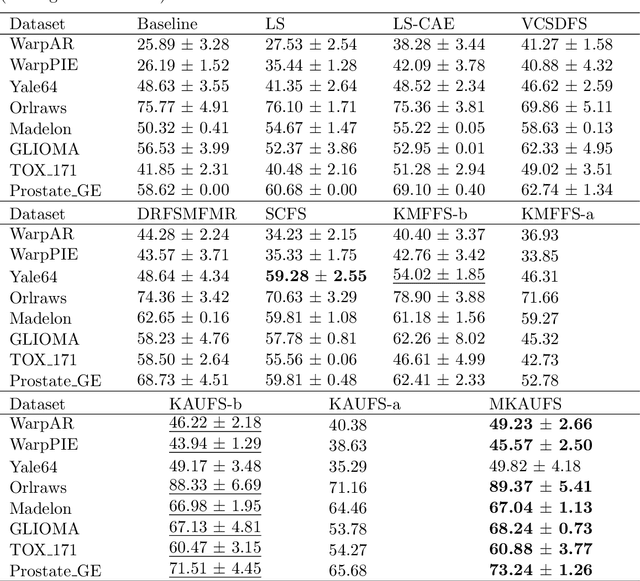
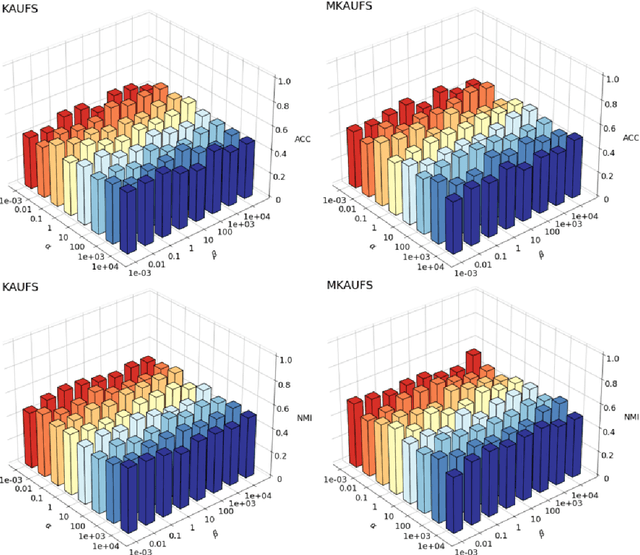
By removing irrelevant and redundant features, feature selection aims to find a good representation of the original features. With the prevalence of unlabeled data, unsupervised feature selection has been proven effective in alleviating the so-called curse of dimensionality. Most existing matrix factorization-based unsupervised feature selection methods are built upon subspace learning, but they have limitations in capturing nonlinear structural information among features. It is well-known that kernel techniques can capture nonlinear structural information. In this paper, we construct a model by integrating kernel functions and kernel alignment, which can be equivalently characterized as a matrix factorization problem. However, such an extension raises another issue: the algorithm performance heavily depends on the choice of kernel, which is often unknown a priori. Therefore, we further propose a multiple kernel-based learning method. By doing so, our model can learn both linear and nonlinear similarity information and automatically generate the most appropriate kernel. Experimental analysis on real-world data demonstrates that the two proposed methods outperform other classic and state-of-the-art unsupervised feature selection methods in terms of clustering results and redundancy reduction in almost all datasets tested.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge