Kernel Alignment for Unsupervised Feature Selection via Matrix Factorization

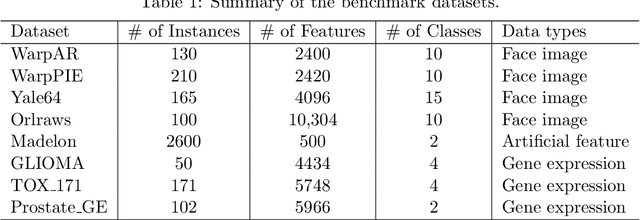
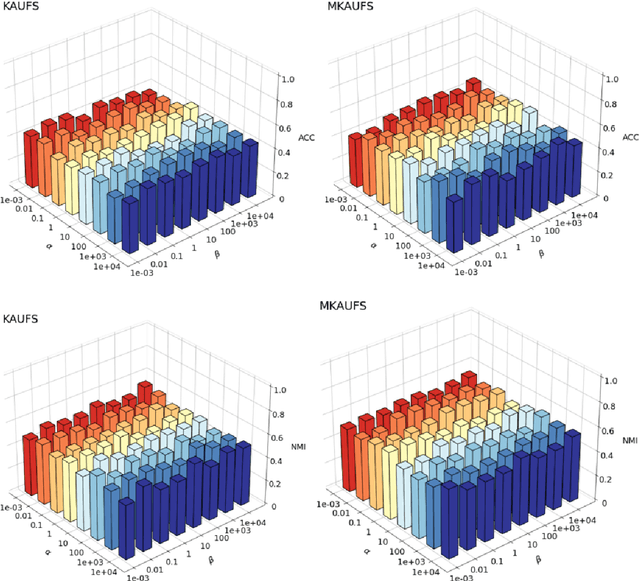
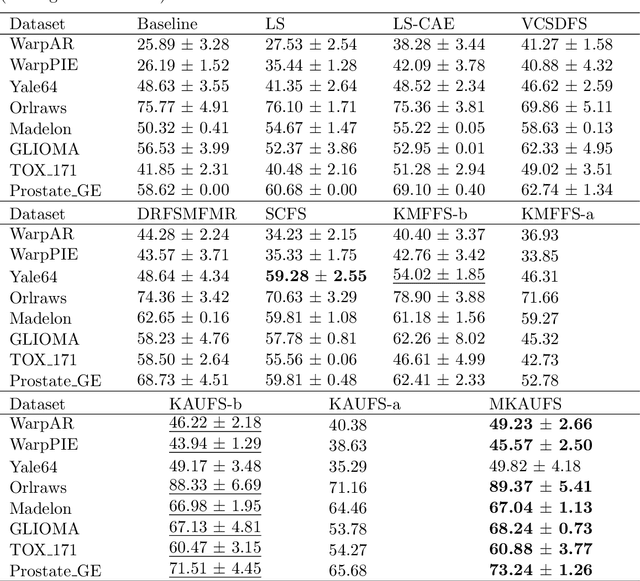
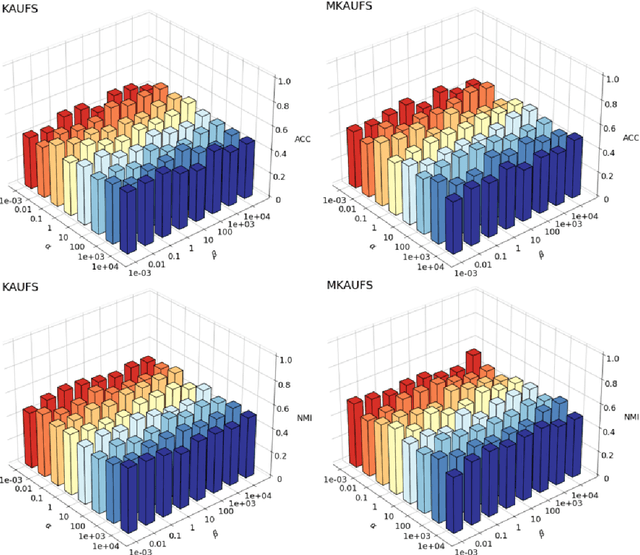
By removing irrelevant and redundant features, feature selection aims to find a good representation of the original features. With the prevalence of unlabeled data, unsupervised feature selection has been proven effective in alleviating the so-called curse of dimensionality. Most existing matrix factorization-based unsupervised feature selection methods are built upon subspace learning, but they have limitations in capturing nonlinear structural information among features. It is well-known that kernel techniques can capture nonlinear structural information. In this paper, we construct a model by integrating kernel functions and kernel alignment, which can be equivalently characterized as a matrix factorization problem. However, such an extension raises another issue: the algorithm performance heavily depends on the choice of kernel, which is often unknown a priori. Therefore, we further propose a multiple kernel-based learning method. By doing so, our model can learn both linear and nonlinear similarity information and automatically generate the most appropriate kernel. Experimental analysis on real-world data demonstrates that the two proposed methods outperform other classic and state-of-the-art unsupervised feature selection methods in terms of clustering results and redundancy reduction in almost all datasets tested.

Comparison of Deep Learning Segmentation and Multigrader-annotated Mandibular Canals of Multicenter CBCT scans

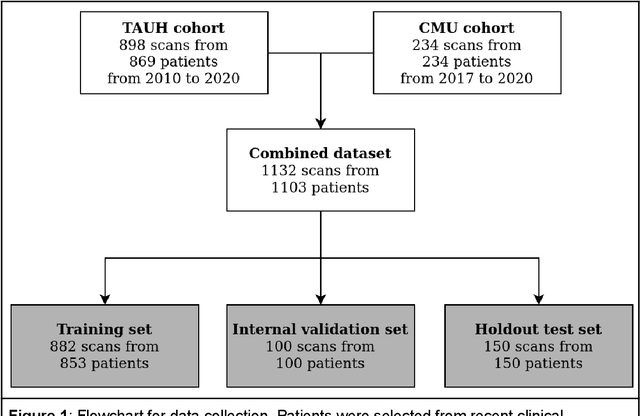
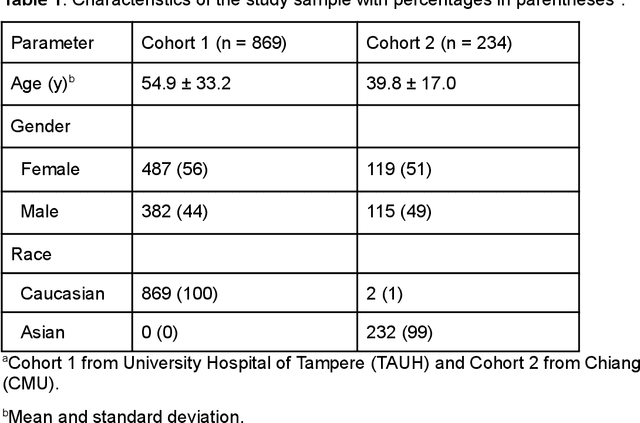
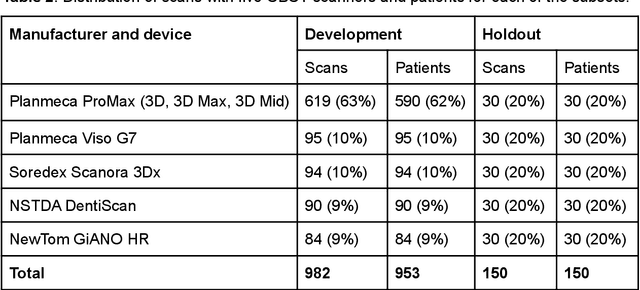
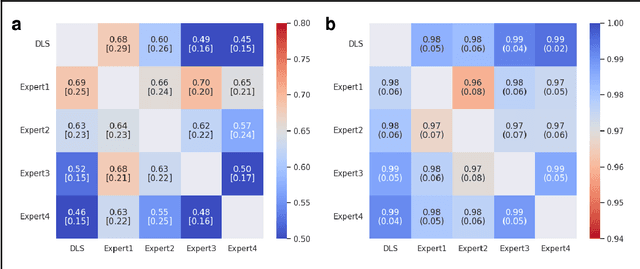
Deep learning approach has been demonstrated to automatically segment the bilateral mandibular canals from CBCT scans, yet systematic studies of its clinical and technical validation are scarce. To validate the mandibular canal localization accuracy of a deep learning system (DLS) we trained it with 982 CBCT scans and evaluated using 150 scans of five scanners from clinical workflow patients of European and Southeast Asian Institutes, annotated by four radiologists. The interobserver variability was compared to the variability between the DLS and the radiologists. In addition, the generalization of DLS to CBCT scans from scanners not used in the training data was examined to evaluate the out-of-distribution generalization capability. The DLS had lower variability to the radiologists than the interobserver variability between them and it was able to generalize to three new devices. For the radiologists' consensus segmentation, used as gold standard, the DLS had a symmetric mean curve distance of 0.39 mm compared to those of the individual radiologists with 0.62 mm, 0.55 mm, 0.47 mm, and 0.42 mm. The DLS showed comparable or slightly better performance in the segmentation of the mandibular canal with the radiologists and generalization capability to new scanners.

Peacock Bundles: Bundle Coloring for Graphs with Globality-Locality Trade-off

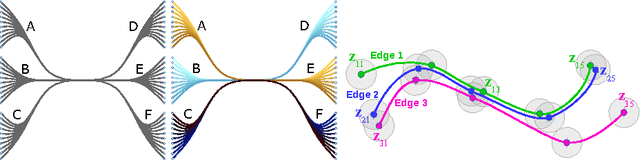
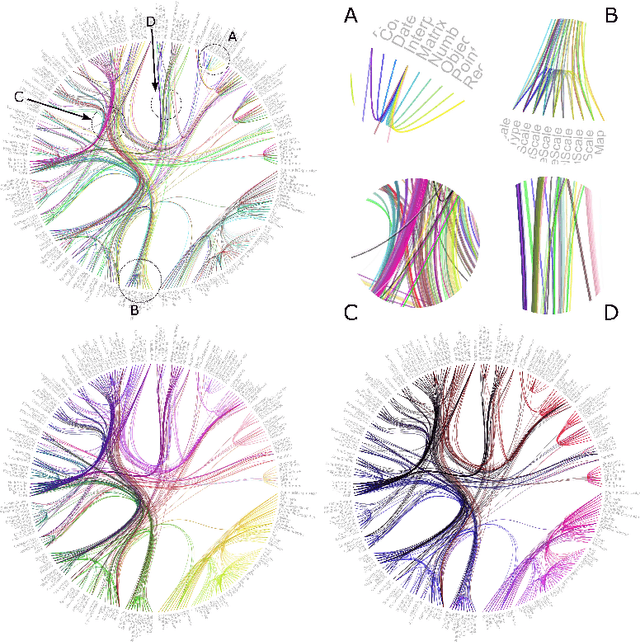
Bundling of graph edges (node-to-node connections) is a common technique to enhance visibility of overall trends in the edge structure of a large graph layout, and a large variety of bundling algorithms have been proposed. However, with strong bundling, it becomes hard to identify origins and destinations of individual edges. We propose a solution: we optimize edge coloring to differentiate bundled edges. We quantify strength of bundling in a flexible pairwise fashion between edges, and among bundled edges, we quantify how dissimilar their colors should be by dissimilarity of their origins and destinations. We solve the resulting nonlinear optimization, which is also interpretable as a novel dimensionality reduction task. In large graphs the necessary compromise is whether to differentiate colors sharply between locally occurring strongly bundled edges ("local bundles"), or also between the weakly bundled edges occurring globally over the graph ("global bundles"); we allow a user-set global-local tradeoff. We call the technique "peacock bundles". Experiments show the coloring clearly enhances comprehensibility of graph layouts with edge bundling.

An Information Retrieval Approach to Finding Dependent Subspaces of Multiple Views

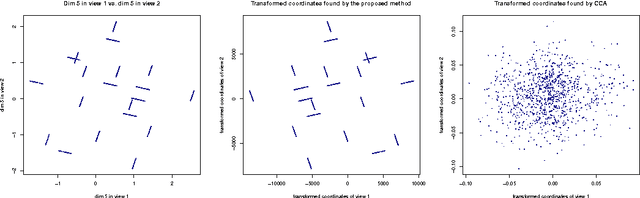
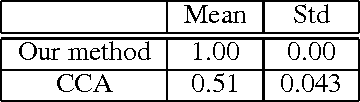
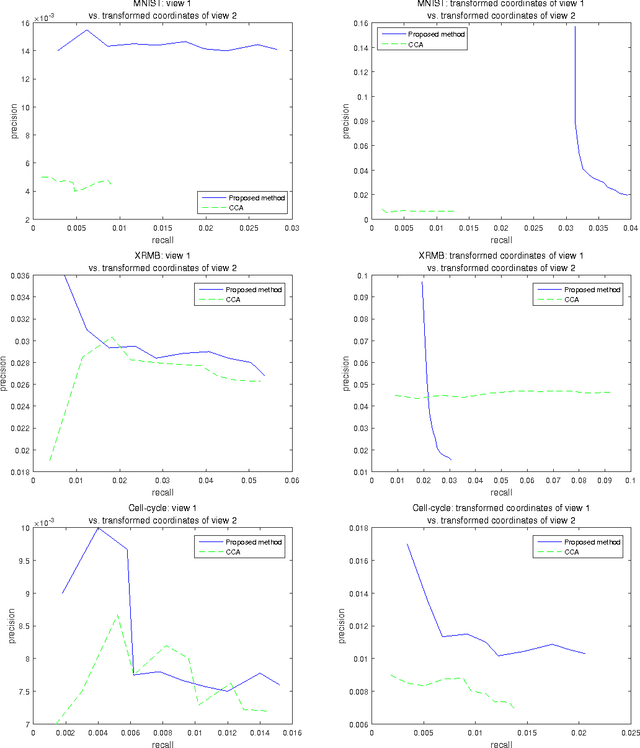
Finding relationships between multiple views of data is essential both for exploratory analysis and as pre-processing for predictive tasks. A prominent approach is to apply variants of Canonical Correlation Analysis (CCA), a classical method seeking correlated components between views. The basic CCA is restricted to maximizing a simple dependency criterion, correlation, measured directly between data coordinates. We introduce a new method that finds dependent subspaces of views directly optimized for the data analysis task of \textit{neighbor retrieval between multiple views}. We optimize mappings for each view such as linear transformations to maximize cross-view similarity between neighborhoods of data samples. The criterion arises directly from the well-defined retrieval task, detects nonlinear and local similarities, is able to measure dependency of data relationships rather than only individual data coordinates, and is related to well understood measures of information retrieval quality. In experiments we show the proposed method outperforms alternatives in preserving cross-view neighborhood similarities, and yields insights into local dependencies between multiple views.