Curvature Corrected Nonnegative Manifold Data Factorization

Data with underlying nonlinear structure are collected across numerous application domains, necessitating new data processing and analysis methods adapted to nonlinear domain structure. Riemannanian manifolds present a rich environment in which to develop such tools, as manifold-valued data arise in a variety of scientific settings, and Riemannian geometry provides a solid theoretical grounding for geometric data analysis. Low-rank approximations, such as nonnegative matrix factorization (NMF), are the foundation of many Euclidean data analysis methods, so adaptations of these factorizations for manifold-valued data are important building blocks for further development of manifold data analysis. In this work, we propose curvature corrected nonnegative manifold data factorization (CC-NMDF) as a geometry-aware method for extracting interpretable factors from manifold-valued data, analogous to nonnegative matrix factorization. We develop an efficient iterative algorithm for computing CC-NMDF and demonstrate our method on real-world diffusion tensor magnetic resonance imaging data.

Pullback Flow Matching on Data Manifolds

We propose Pullback Flow Matching (PFM), a novel framework for generative modeling on data manifolds. Unlike existing methods that assume or learn restrictive closed-form manifold mappings for training Riemannian Flow Matching (RFM) models, PFM leverages pullback geometry and isometric learning to preserve the underlying manifold's geometry while enabling efficient generation and precise interpolation in latent space. This approach not only facilitates closed-form mappings on the data manifold but also allows for designable latent spaces, using assumed metrics on both data and latent manifolds. By enhancing isometric learning through Neural ODEs and proposing a scalable training objective, we achieve a latent space more suitable for interpolation, leading to improved manifold learning and generative performance. We demonstrate PFM's effectiveness through applications in synthetic data, protein dynamics and protein sequence data, generating novel proteins with specific properties. This method shows strong potential for drug discovery and materials science, where generating novel samples with specific properties is of great interest.

Score-based pullback Riemannian geometry

Data-driven Riemannian geometry has emerged as a powerful tool for interpretable representation learning, offering improved efficiency in downstream tasks. Moving forward, it is crucial to balance cheap manifold mappings with efficient training algorithms. In this work, we integrate concepts from pullback Riemannian geometry and generative models to propose a framework for data-driven Riemannian geometry that is scalable in both geometry and learning: score-based pullback Riemannian geometry. Focusing on unimodal distributions as a first step, we propose a score-based Riemannian structure with closed-form geodesics that pass through the data probability density. With this structure, we construct a Riemannian autoencoder (RAE) with error bounds for discovering the correct data manifold dimension. This framework can naturally be used with anisotropic normalizing flows by adopting isometry regularization during training. Through numerical experiments on various datasets, we demonstrate that our framework not only produces high-quality geodesics through the data support, but also reliably estimates the intrinsic dimension of the data manifold and provides a global chart of the manifold, even in high-dimensional ambient spaces.

Pulling back symmetric Riemannian geometry for data analysis

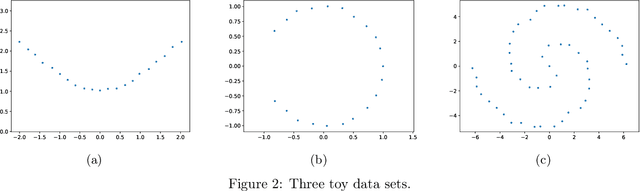
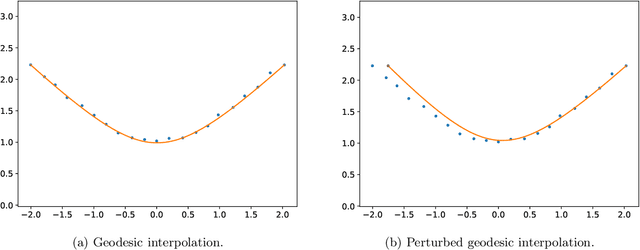
Data sets tend to live in low-dimensional non-linear subspaces. Ideal data analysis tools for such data sets should therefore account for such non-linear geometry. The symmetric Riemannian geometry setting can be suitable for a variety of reasons. First, it comes with a rich mathematical structure to account for a wide range of non-linear geometries that has been shown to be able to capture the data geometry through empirical evidence from classical non-linear embedding. Second, many standard data analysis tools initially developed for data in Euclidean space can also be generalised efficiently to data on a symmetric Riemannian manifold. A conceptual challenge comes from the lack of guidelines for constructing a symmetric Riemannian structure on the data space itself and the lack of guidelines for modifying successful algorithms on symmetric Riemannian manifolds for data analysis to this setting. This work considers these challenges in the setting of pullback Riemannian geometry through a diffeomorphism. The first part of the paper characterises diffeomorphisms that result in proper, stable and efficient data analysis. The second part then uses these best practices to guide construction of such diffeomorphisms through deep learning. As a proof of concept, different types of pullback geometries -- among which the proposed construction -- are tested on several data analysis tasks and on several toy data sets. The numerical experiments confirm the predictions from theory, i.e., that the diffeomorphisms generating the pullback geometry need to map the data manifold into a geodesic subspace of the pulled back Riemannian manifold while preserving local isometry around the data manifold for proper, stable and efficient data analysis, and that pulling back positive curvature can be problematic in terms of stability.

Spectral decomposition of atomic structures in heterogeneous cryo-EM

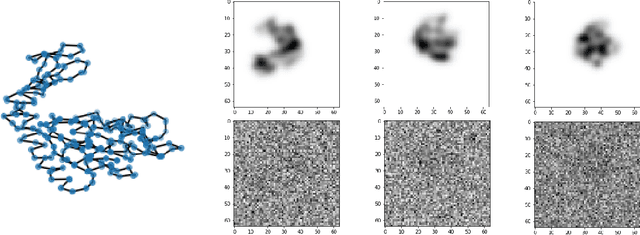
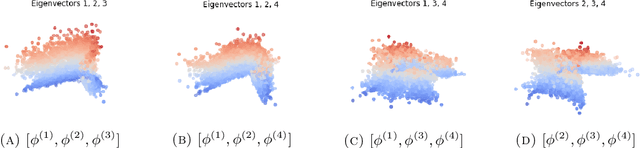
We consider the problem of recovering the three-dimensional atomic structure of a flexible macromolecule from a heterogeneous cryo-EM dataset. The dataset contains noisy tomographic projections of the electrostatic potential of the macromolecule, taken from different viewing directions, and in the heterogeneous case, each image corresponds to a different conformation of the macromolecule. Under the assumption that the macromolecule can be modelled as a chain, or discrete curve (as it is for instance the case for a protein backbone with a single chain of amino-acids), we introduce a method to estimate the deformation of the atomic model with respect to a given conformation, which is assumed to be known a priori. Our method consists on estimating the torsion and bond angles of the atomic model in each conformation as a linear combination of the eigenfunctions of the Laplace operator in the manifold of conformations. These eigenfunctions can be approximated by means of a well-known technique in manifold learning, based on the construction of a graph Laplacian using the cryo-EM dataset. Finally, we test our approach with synthetic datasets, for which we recover the atomic model of two-dimensional and three-dimensional flexible structures from noisy tomographic projections.