FedMAP: Unlocking Potential in Personalized Federated Learning through Bi-Level MAP Optimization

Federated Learning (FL) enables collaborative training of machine learning models on decentralized data while preserving data privacy. However, data across clients often differs significantly due to class imbalance, feature distribution skew, sample size imbalance, and other phenomena. Leveraging information from these not identically distributed (non-IID) datasets poses substantial challenges. FL methods based on a single global model cannot effectively capture the variations in client data and underperform in non-IID settings. Consequently, Personalized FL (PFL) approaches that adapt to each client's data distribution but leverage other clients' data are essential but currently underexplored. We propose a novel Bayesian PFL framework using bi-level optimization to tackle the data heterogeneity challenges. Our proposed framework utilizes the global model as a prior distribution within a Maximum A Posteriori (MAP) estimation of personalized client models. This approach facilitates PFL by integrating shared knowledge from the prior, thereby enhancing local model performance, generalization ability, and communication efficiency. We extensively evaluated our bi-level optimization approach on real-world and synthetic datasets, demonstrating significant improvements in model accuracy compared to existing methods while reducing communication overhead. This study contributes to PFL by establishing a solid theoretical foundation for the proposed method and offering a robust, ready-to-use framework that effectively addresses the challenges posed by non-IID data in FL.

Spectral decomposition of atomic structures in heterogeneous cryo-EM

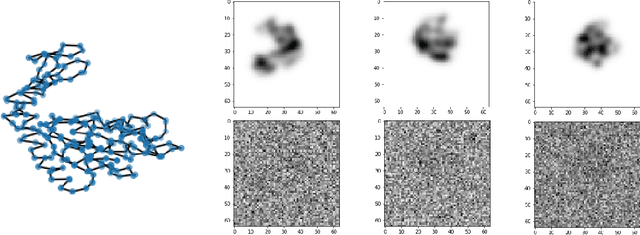
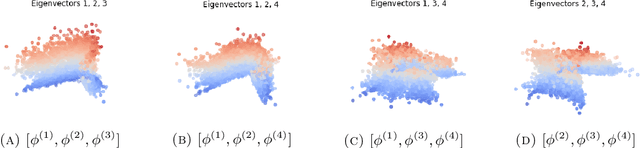
We consider the problem of recovering the three-dimensional atomic structure of a flexible macromolecule from a heterogeneous cryo-EM dataset. The dataset contains noisy tomographic projections of the electrostatic potential of the macromolecule, taken from different viewing directions, and in the heterogeneous case, each image corresponds to a different conformation of the macromolecule. Under the assumption that the macromolecule can be modelled as a chain, or discrete curve (as it is for instance the case for a protein backbone with a single chain of amino-acids), we introduce a method to estimate the deformation of the atomic model with respect to a given conformation, which is assumed to be known a priori. Our method consists on estimating the torsion and bond angles of the atomic model in each conformation as a linear combination of the eigenfunctions of the Laplace operator in the manifold of conformations. These eigenfunctions can be approximated by means of a well-known technique in manifold learning, based on the construction of a graph Laplacian using the cryo-EM dataset. Finally, we test our approach with synthetic datasets, for which we recover the atomic model of two-dimensional and three-dimensional flexible structures from noisy tomographic projections.