Spectral decomposition of atomic structures in heterogeneous cryo-EM
Paper and Code
Sep 12, 2022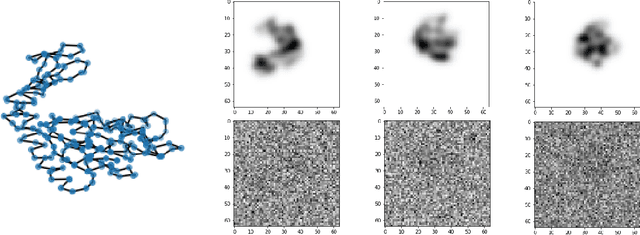


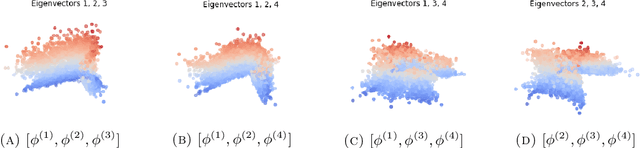
We consider the problem of recovering the three-dimensional atomic structure of a flexible macromolecule from a heterogeneous cryo-EM dataset. The dataset contains noisy tomographic projections of the electrostatic potential of the macromolecule, taken from different viewing directions, and in the heterogeneous case, each image corresponds to a different conformation of the macromolecule. Under the assumption that the macromolecule can be modelled as a chain, or discrete curve (as it is for instance the case for a protein backbone with a single chain of amino-acids), we introduce a method to estimate the deformation of the atomic model with respect to a given conformation, which is assumed to be known a priori. Our method consists on estimating the torsion and bond angles of the atomic model in each conformation as a linear combination of the eigenfunctions of the Laplace operator in the manifold of conformations. These eigenfunctions can be approximated by means of a well-known technique in manifold learning, based on the construction of a graph Laplacian using the cryo-EM dataset. Finally, we test our approach with synthetic datasets, for which we recover the atomic model of two-dimensional and three-dimensional flexible structures from noisy tomographic projections.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge