Score-based pullback Riemannian geometry

Data-driven Riemannian geometry has emerged as a powerful tool for interpretable representation learning, offering improved efficiency in downstream tasks. Moving forward, it is crucial to balance cheap manifold mappings with efficient training algorithms. In this work, we integrate concepts from pullback Riemannian geometry and generative models to propose a framework for data-driven Riemannian geometry that is scalable in both geometry and learning: score-based pullback Riemannian geometry. Focusing on unimodal distributions as a first step, we propose a score-based Riemannian structure with closed-form geodesics that pass through the data probability density. With this structure, we construct a Riemannian autoencoder (RAE) with error bounds for discovering the correct data manifold dimension. This framework can naturally be used with anisotropic normalizing flows by adopting isometry regularization during training. Through numerical experiments on various datasets, we demonstrate that our framework not only produces high-quality geodesics through the data support, but also reliably estimates the intrinsic dimension of the data manifold and provides a global chart of the manifold, even in high-dimensional ambient spaces.

Variational Diffusion Auto-encoder: Deep Latent Variable Model with Unconditional Diffusion Prior

Variational auto-encoders (VAEs) are one of the most popular approaches to deep generative modeling. Despite their success, images generated by VAEs are known to suffer from blurriness, due to a highly unrealistic modeling assumption that the conditional data distribution $ p(\textbf{x} | \textbf{z})$ can be approximated as an isotropic Gaussian. In this work we introduce a principled approach to modeling the conditional data distribution $p(\textbf{x} | \textbf{z})$ by incorporating a diffusion model. We show that it is possible to create a VAE-like deep latent variable model without making the Gaussian assumption on $ p(\textbf{x} | \textbf{z}) $ or even training a decoder network. A trained encoder and an unconditional diffusion model can be combined via Bayes' rule for score functions to obtain an expressive model for $ p(\textbf{x} | \textbf{z}) $. Our approach avoids making strong assumptions on the parametric form of $ p(\textbf{x} | \textbf{z}) $, and thus allows to significantly improve the performance of VAEs.

Your diffusion model secretly knows the dimension of the data manifold

In this work, we propose a novel framework for estimating the dimension of the data manifold using a trained diffusion model. A trained diffusion model approximates the gradient of the log density of a noise-corrupted version of the target distribution for varying levels of corruption. If the data concentrates around a manifold embedded in the high-dimensional ambient space, then as the level of corruption decreases, the score function points towards the manifold, as this direction becomes the direction of maximum likelihood increase. Therefore, for small levels of corruption, the diffusion model provides us with access to an approximation of the normal bundle of the data manifold. This allows us to estimate the dimension of the tangent space, thus, the intrinsic dimension of the data manifold. Our method outperforms linear methods for dimensionality detection such as PPCA in controlled experiments.

Non-Uniform Diffusion Models

Diffusion models have emerged as one of the most promising frameworks for deep generative modeling. In this work, we explore the potential of non-uniform diffusion models. We show that non-uniform diffusion leads to multi-scale diffusion models which have similar structure to this of multi-scale normalizing flows. We experimentally find that in the same or less training time, the multi-scale diffusion model achieves better FID score than the standard uniform diffusion model. More importantly, it generates samples $4.4$ times faster in $128\times 128$ resolution. The speed-up is expected to be higher in higher resolutions where more scales are used. Moreover, we show that non-uniform diffusion leads to a novel estimator for the conditional score function which achieves on par performance with the state-of-the-art conditional denoising estimator. Our theoretical and experimental findings are accompanied by an open source library MSDiff which can facilitate further research of non-uniform diffusion models.

Conditional Image Generation with Score-Based Diffusion Models

Score-based diffusion models have emerged as one of the most promising frameworks for deep generative modelling. In this work we conduct a systematic comparison and theoretical analysis of different approaches to learning conditional probability distributions with score-based diffusion models. In particular, we prove results which provide a theoretical justification for one of the most successful estimators of the conditional score. Moreover, we introduce a multi-speed diffusion framework, which leads to a new estimator for the conditional score, performing on par with previous state-of-the-art approaches. Our theoretical and experimental findings are accompanied by an open source library MSDiff which allows for application and further research of multi-speed diffusion models.

CAFLOW: Conditional Autoregressive Flows

We introduce CAFLOW, a new diverse image-to-image translation model that simultaneously leverages the power of auto-regressive modeling and the modeling efficiency of conditional normalizing flows. We transform the conditioning image into a sequence of latent encodings using a multi-scale normalizing flow and repeat the process for the conditioned image. We model the conditional distribution of the latent encodings by modeling the auto-regressive distributions with an efficient multi-scale normalizing flow, where each conditioning factor affects image synthesis at its respective resolution scale. Our proposed framework performs well on a range of image-to-image translation tasks. It outperforms former designs of conditional flows because of its expressive auto-regressive structure.

How to distribute data across tasks for meta-learning?

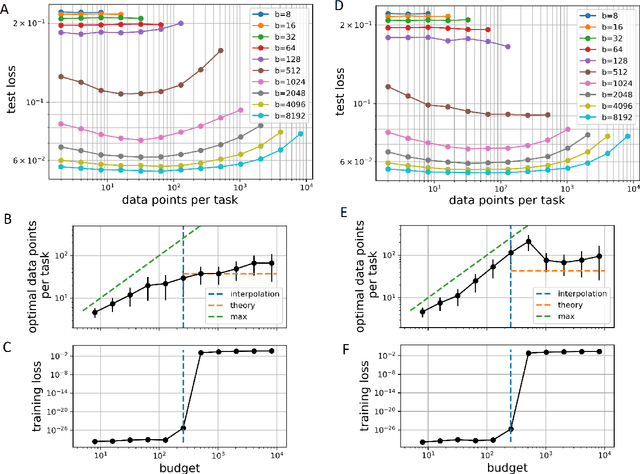
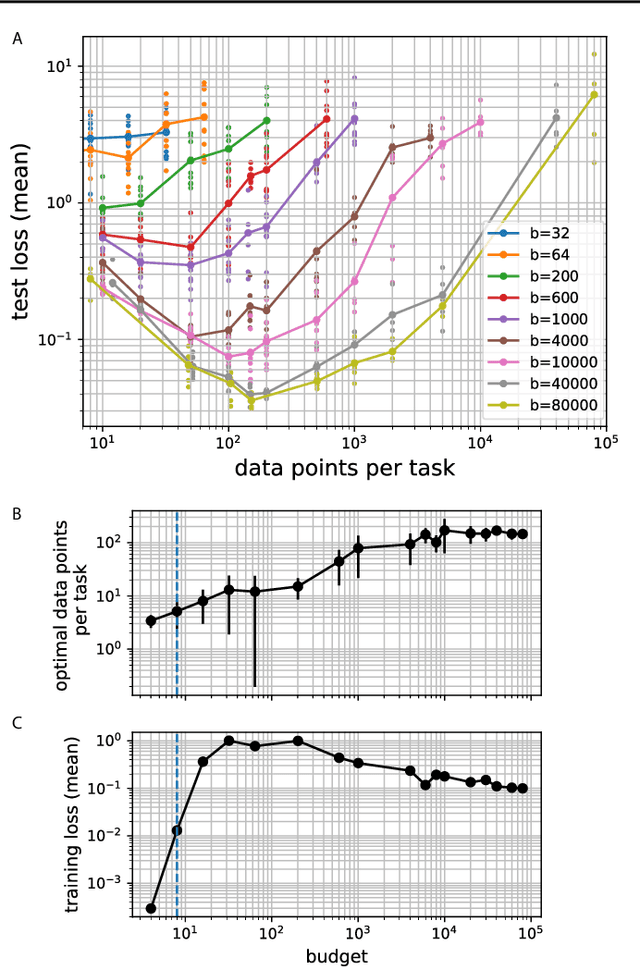
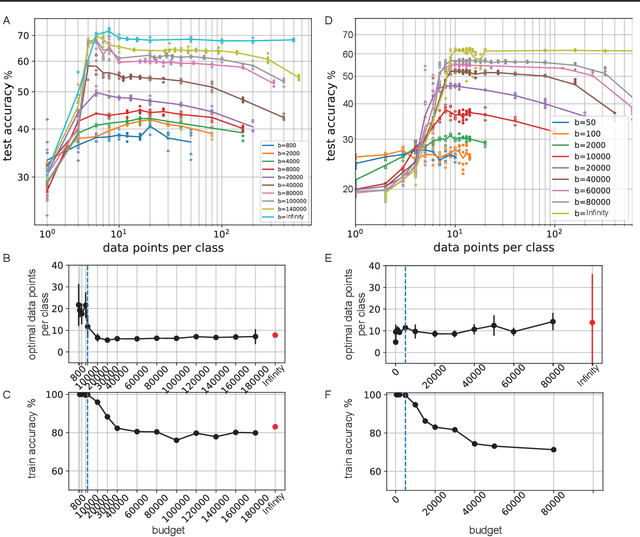
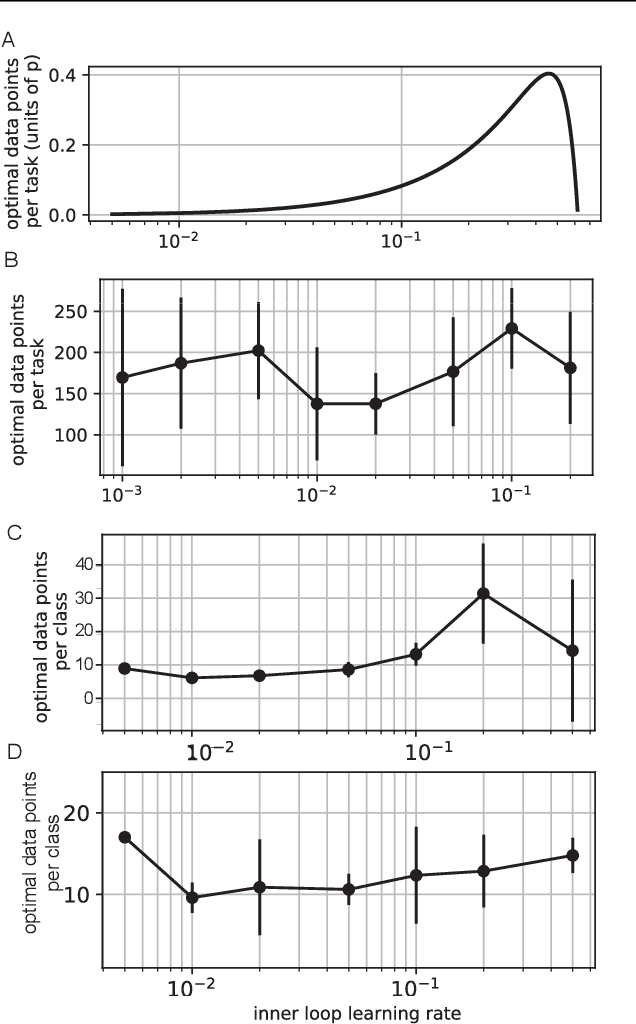
Meta-learning models transfer the knowledge acquired from previous tasks to quickly learn new ones. They are tested on benchmarks with a fixed number of data points per training task. This number is usually arbitrary and it is unknown how it affects the performance. Since labelling of data is expensive, finding the optimal allocation of labels across training tasks may reduce costs: given a fixed budget of labels, should we use a small number of highly labelled tasks, or many tasks with few labels each? We show that: 1) The optimal number of data points per task depends on the budget, but it converges to a unique constant value for large budgets; 2) Convergence occurs around the interpolation threshold of the model. We prove our results mathematically on mixed linear regression, and we show empirically that the same results hold for nonlinear regression and few-shot image classification on CIFAR-FS and mini-ImageNet. Our results suggest a simple and efficient procedure for data collection: the optimal allocation of data can be computed at low cost, by using relatively small data, and collection of additional data can be optimized by the knowledge of the optimal allocation.