A Lipschitz spaces view of infinitely wide shallow neural networks

We revisit the mean field parametrization of shallow neural networks, using signed measures on unbounded parameter spaces and duality pairings that take into account the regularity and growth of activation functions. This setting directly leads to the use of unbalanced Kantorovich-Rubinstein norms defined by duality with Lipschitz functions, and of spaces of measures dual to those of continuous functions with controlled growth. These allow to make transparent the need for total variation and moment bounds or penalization to obtain existence of minimizers of variational formulations, under which we prove a compactness result in strong Kantorovich-Rubinstein norm, and in the absence of which we show several examples demonstrating undesirable behavior. Further, the Kantorovich-Rubinstein setting enables us to combine the advantages of a completely linear parametrization and ensuing reproducing kernel Banach space framework with optimal transport insights. We showcase this synergy with representer theorems and uniform large data limits for empirical risk minimization, and in proposed formulations for distillation and fusion applications.

Unsupervised approaches based on optimal transport and convex analysis for inverse problems in imaging

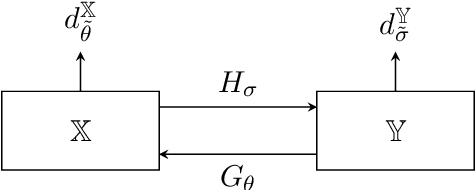
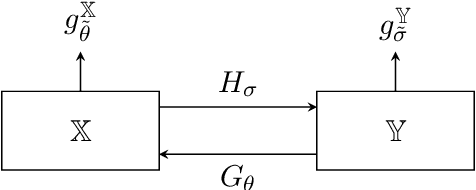
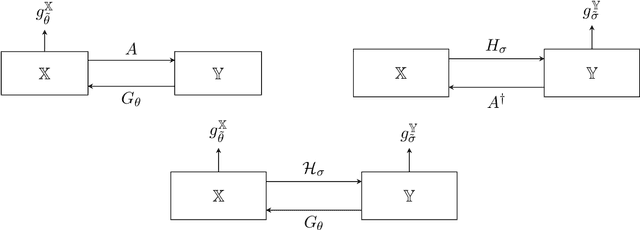
Unsupervised deep learning approaches have recently become one of the crucial research areas in imaging owing to their ability to learn expressive and powerful reconstruction operators even when paired high-quality training data is scarcely available. In this chapter, we review theoretically principled unsupervised learning schemes for solving imaging inverse problems, with a particular focus on methods rooted in optimal transport and convex analysis. We begin by reviewing the optimal transport-based unsupervised approaches such as the cycle-consistency-based models and learned adversarial regularization methods, which have clear probabilistic interpretations. Subsequently, we give an overview of a recent line of works on provably convergent learned optimization algorithms applied to accelerate the solution of imaging inverse problems, alongside their dedicated unsupervised training schemes. We also survey a number of provably convergent plug-and-play algorithms (based on gradient-step deep denoisers), which are among the most important and widely applied unsupervised approaches for imaging problems. At the end of this survey, we provide an overview of a few related unsupervised learning frameworks that complement our focused schemes. Together with a detailed survey, we provide an overview of the key mathematical results that underlie the methods reviewed in the chapter to keep our discussion self-contained.

Implicit neural representations for unsupervised super-resolution and denoising of 4D flow MRI

4D flow MRI is a non-invasive imaging method that can measure blood flow velocities over time. However, the velocity fields detected by this technique have limitations due to low resolution and measurement noise. Coordinate-based neural networks have been researched to improve accuracy, with SIRENs being suitable for super-resolution tasks. Our study investigates SIRENs for time-varying 3-directional velocity fields measured in the aorta by 4D flow MRI, achieving denoising and super-resolution. We trained our method on voxel coordinates and benchmarked our approach using synthetic measurements and a real 4D flow MRI scan. Our optimized SIREN architecture outperformed state-of-the-art techniques, producing denoised and super-resolved velocity fields from clinical data. Our approach is quick to execute and straightforward to implement for novel cases, achieving 4D super-resolution.

End-to-end reconstruction meets data-driven regularization for inverse problems

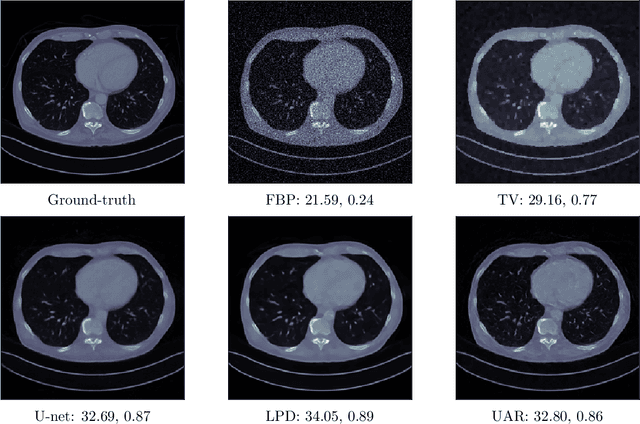
We propose an unsupervised approach for learning end-to-end reconstruction operators for ill-posed inverse problems. The proposed method combines the classical variational framework with iterative unrolling, which essentially seeks to minimize a weighted combination of the expected distortion in the measurement space and the Wasserstein-1 distance between the distributions of the reconstruction and ground-truth. More specifically, the regularizer in the variational setting is parametrized by a deep neural network and learned simultaneously with the unrolled reconstruction operator. The variational problem is then initialized with the reconstruction of the unrolled operator and solved iteratively till convergence. Notably, it takes significantly fewer iterations to converge, thanks to the excellent initialization obtained via the unrolled operator. The resulting approach combines the computational efficiency of end-to-end unrolled reconstruction with the well-posedness and noise-stability guarantees of the variational setting. Moreover, we demonstrate with the example of X-ray computed tomography (CT) that our approach outperforms state-of-the-art unsupervised methods, and that it outperforms or is on par with state-of-the-art supervised learned reconstruction approaches.

CAFLOW: Conditional Autoregressive Flows

We introduce CAFLOW, a new diverse image-to-image translation model that simultaneously leverages the power of auto-regressive modeling and the modeling efficiency of conditional normalizing flows. We transform the conditioning image into a sequence of latent encodings using a multi-scale normalizing flow and repeat the process for the conditioned image. We model the conditional distribution of the latent encodings by modeling the auto-regressive distributions with an efficient multi-scale normalizing flow, where each conditioning factor affects image synthesis at its respective resolution scale. Our proposed framework performs well on a range of image-to-image translation tasks. It outperforms former designs of conditional flows because of its expressive auto-regressive structure.

Sinkhorn AutoEncoders

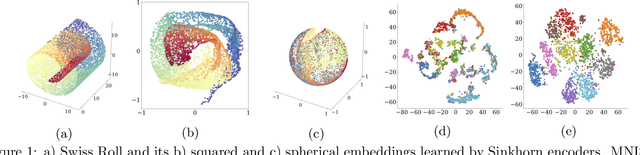
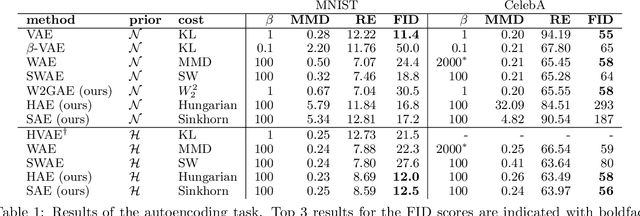
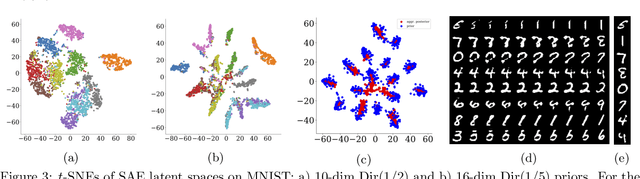
Optimal Transport offers an alternative to maximum likelihood for learning generative autoencoding models. We show how this principle dictates the minimization of the Wasserstein distance between the encoder aggregated posterior and the prior, plus a reconstruction error. We prove that in the non-parametric limit the autoencoder generates the data distribution if and only if the two distributions match exactly, and that the optimum can be obtained by deterministic autoencoders. We then introduce the Sinkhorn AutoEncoder (SAE), which casts the problem into Optimal Transport on the latent space. The resulting Wasserstein distance is minimized by backpropagating through the Sinkhorn algorithm. SAE models the aggregated posterior as an implicit distribution and therefore does not need a reparameterization trick for gradients estimation. Moreover, it requires virtually no adaptation to different prior distributions. We demonstrate its flexibility by considering models with hyperspherical and Dirichlet priors, as well as a simple case of probabilistic programming. SAE matches or outperforms other autoencoding models in visual quality and FID scores.

Loss factorization, weakly supervised learning and label noise robustness

We prove that the empirical risk of most well-known loss functions factors into a linear term aggregating all labels with a term that is label free, and can further be expressed by sums of the loss. This holds true even for non-smooth, non-convex losses and in any RKHS. The first term is a (kernel) mean operator --the focal quantity of this work-- which we characterize as the sufficient statistic for the labels. The result tightens known generalization bounds and sheds new light on their interpretation. Factorization has a direct application on weakly supervised learning. In particular, we demonstrate that algorithms like SGD and proximal methods can be adapted with minimal effort to handle weak supervision, once the mean operator has been estimated. We apply this idea to learning with asymmetric noisy labels, connecting and extending prior work. Furthermore, we show that most losses enjoy a data-dependent (by the mean operator) form of noise robustness, in contrast with known negative results.