Manifold limit for the training of shallow graph convolutional neural networks

We study the discrete-to-continuum consistency of the training of shallow graph convolutional neural networks (GCNNs) on proximity graphs of sampled point clouds under a manifold assumption. Graph convolution is defined spectrally via the graph Laplacian, whose low-frequency spectrum approximates that of the Laplace-Beltrami operator of the underlying smooth manifold, and shallow GCNNs of possibly infinite width are linear functionals on the space of measures on the parameter space. From this functional-analytic perspective, graph signals are seen as spatial discretizations of functions on the manifold, which leads to a natural notion of training data consistent across graph resolutions. To enable convergence results, the continuum parameter space is chosen as a weakly compact product of unit balls, with Sobolev regularity imposed on the output weight and bias, but not on the convolutional parameter. The corresponding discrete parameter spaces inherit the corresponding spectral decay, and are additionally restricted by a frequency cutoff adapted to the informative spectral window of the graph Laplacians. Under these assumptions, we prove $Γ$-convergence of regularized empirical risk minimization functionals and corresponding convergence of their global minimizers, in the sense of weak convergence of the parameter measures and uniform convergence of the functions over compact sets. This provides a formalization of mesh and sample independence for the training of such networks.

A Lipschitz spaces view of infinitely wide shallow neural networks

We revisit the mean field parametrization of shallow neural networks, using signed measures on unbounded parameter spaces and duality pairings that take into account the regularity and growth of activation functions. This setting directly leads to the use of unbalanced Kantorovich-Rubinstein norms defined by duality with Lipschitz functions, and of spaces of measures dual to those of continuous functions with controlled growth. These allow to make transparent the need for total variation and moment bounds or penalization to obtain existence of minimizers of variational formulations, under which we prove a compactness result in strong Kantorovich-Rubinstein norm, and in the absence of which we show several examples demonstrating undesirable behavior. Further, the Kantorovich-Rubinstein setting enables us to combine the advantages of a completely linear parametrization and ensuing reproducing kernel Banach space framework with optimal transport insights. We showcase this synergy with representer theorems and uniform large data limits for empirical risk minimization, and in proposed formulations for distillation and fusion applications.

Convective regularization for optical flow

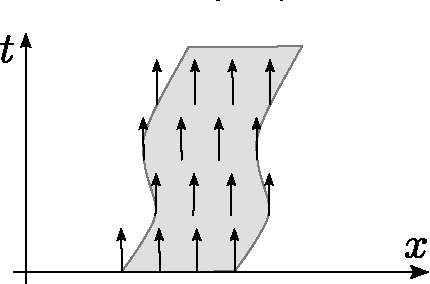
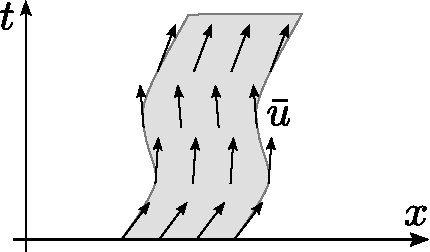
We argue that the time derivative in a fixed coordinate frame may not be the most appropriate measure of time regularity of an optical flow field. Instead, for a given velocity field $v$ we consider the convective acceleration $v_t + \nabla v v$ which describes the acceleration of objects moving according to $v$. Consequently we investigate the suitability of the nonconvex functional $\|v_t + \nabla v v\|^2_{L^2}$ as a regularization term for optical flow. We demonstrate that this term acts as both a spatial and a temporal regularizer and has an intrinsic edge-preserving property. We incorporate it into a contrast invariant and time-regularized variant of the Horn-Schunck functional, prove existence of minimizers and verify experimentally that it addresses some of the problems of basic quadratic models. For the minimization we use an iterative scheme that approximates the original nonlinear problem with a sequence of linear ones. We believe that the convective acceleration may be gainfully introduced in a variety of optical flow models.