Convective regularization for optical flow

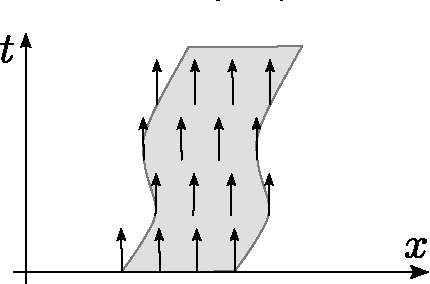
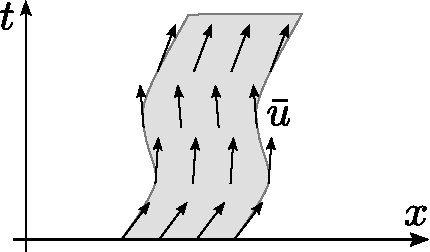
We argue that the time derivative in a fixed coordinate frame may not be the most appropriate measure of time regularity of an optical flow field. Instead, for a given velocity field $v$ we consider the convective acceleration $v_t + \nabla v v$ which describes the acceleration of objects moving according to $v$. Consequently we investigate the suitability of the nonconvex functional $\|v_t + \nabla v v\|^2_{L^2}$ as a regularization term for optical flow. We demonstrate that this term acts as both a spatial and a temporal regularizer and has an intrinsic edge-preserving property. We incorporate it into a contrast invariant and time-regularized variant of the Horn-Schunck functional, prove existence of minimizers and verify experimentally that it addresses some of the problems of basic quadratic models. For the minimization we use an iterative scheme that approximates the original nonlinear problem with a sequence of linear ones. We believe that the convective acceleration may be gainfully introduced in a variety of optical flow models.

Optical Flow on Evolving Surfaces with Space and Time Regularisation

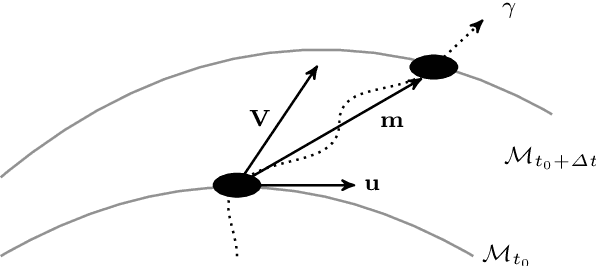
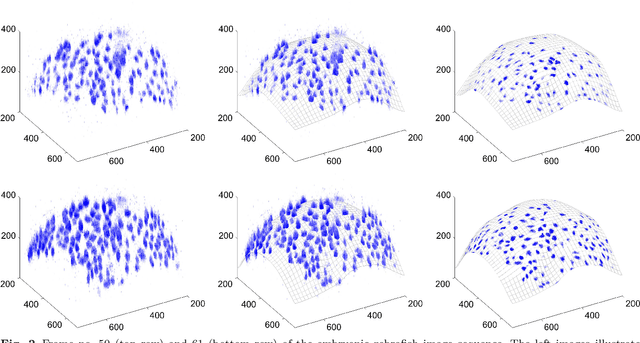
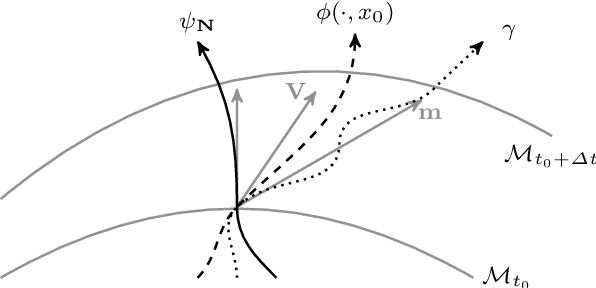
We extend the concept of optical flow with spatiotemporal regularisation to a dynamic non-Euclidean setting. Optical flow is traditionally computed from a sequence of flat images. The purpose of this paper is to introduce variational motion estimation for images that are defined on an evolving surface. Volumetric microscopy images depicting a live zebrafish embryo serve as both biological motivation and test data.

Decomposition of Optical Flow on the Sphere

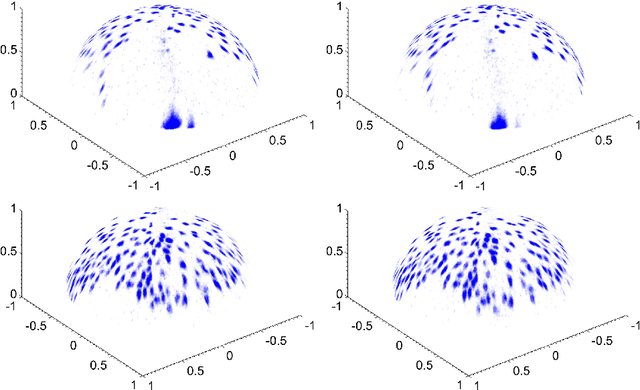
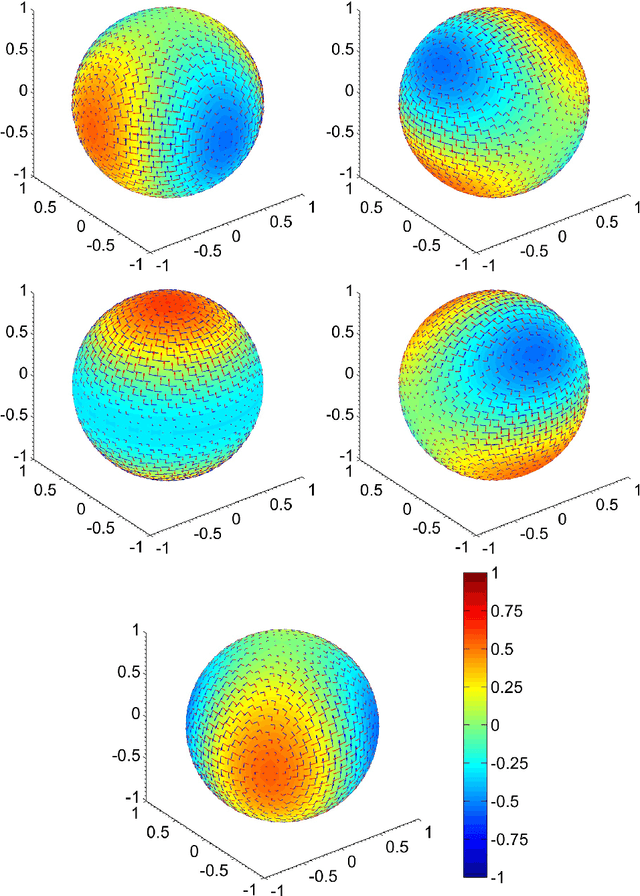
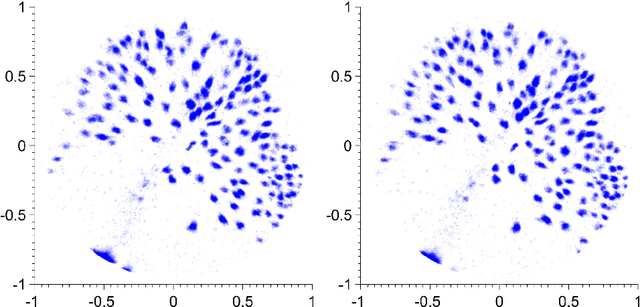
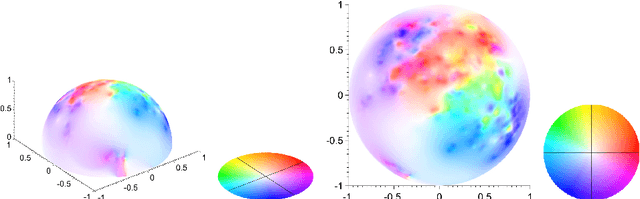
We propose a number of variational regularisation methods for the estimation and decomposition of motion fields on the $2$-sphere. While motion estimation is based on the optical flow equation, the presented decomposition models are motivated by recent trends in image analysis. In particular we treat $u+v$ decomposition as well as hierarchical decomposition. Helmholtz decomposition of motion fields is obtained as a natural by-product of the chosen numerical method based on vector spherical harmonics. All models are tested on time-lapse microscopy data depicting fluorescently labelled endodermal cells of a zebrafish embryo.

Optical Flow on Evolving Surfaces with an Application to the Analysis of 4D Microscopy Data

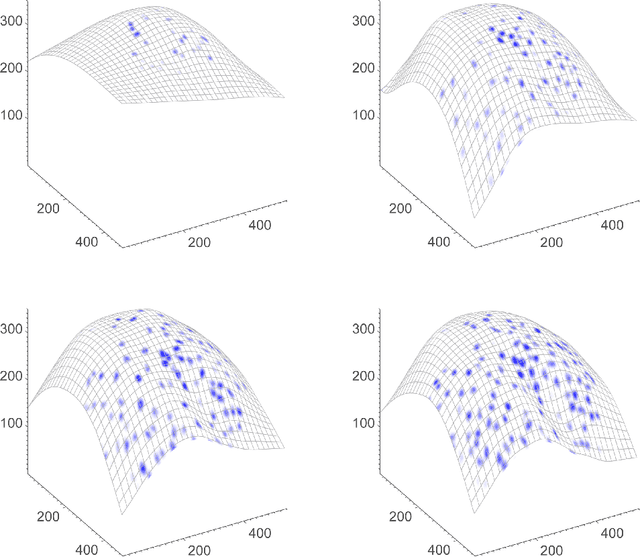
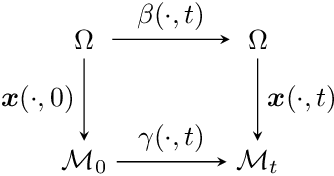
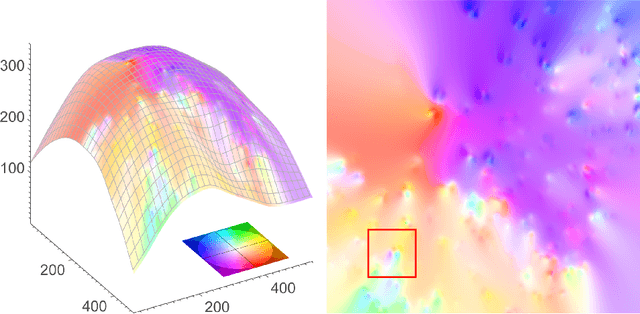
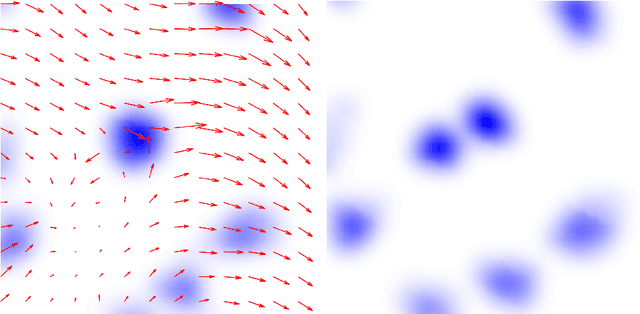
We extend the concept of optical flow to a dynamic non-Euclidean setting. Optical flow is traditionally computed from a sequence of flat images. It is the purpose of this paper to introduce variational motion estimation for images that are defined on an evolving surface. Volumetric microscopy images depicting a live zebrafish embryo serve as both biological motivation and test data.