Decomposition of Optical Flow on the Sphere
Paper and Code
Mar 04, 2014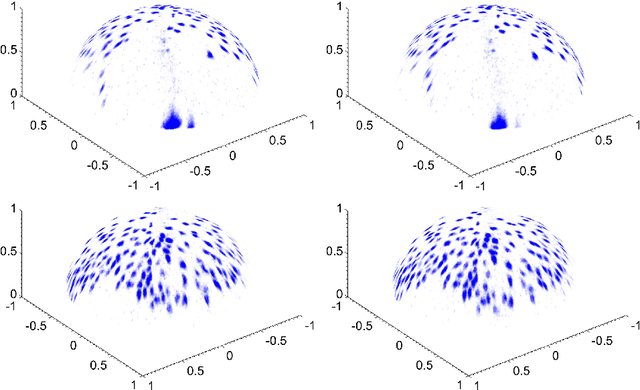
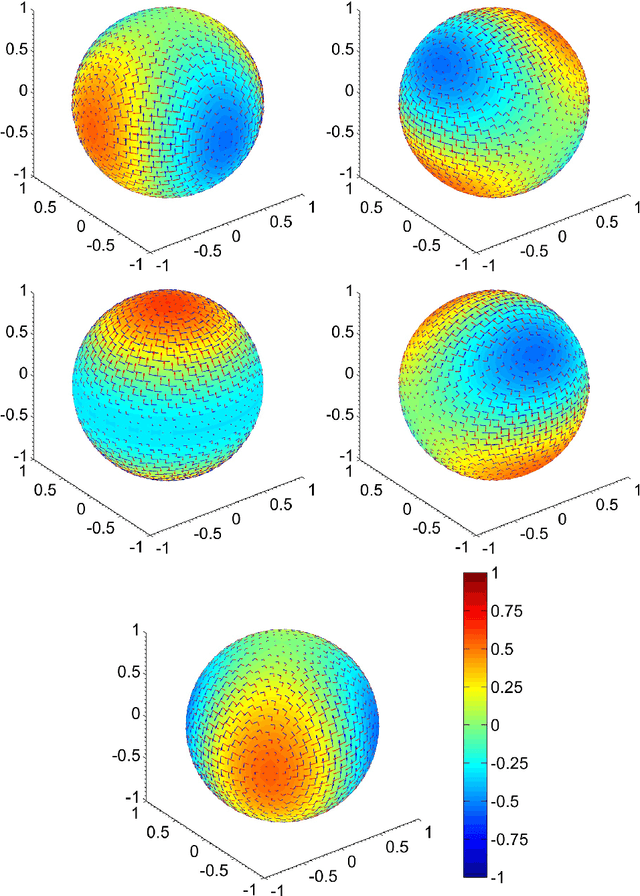
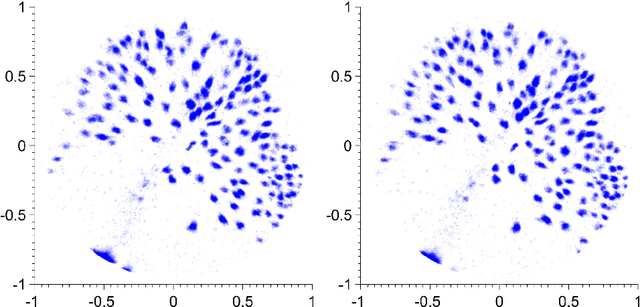
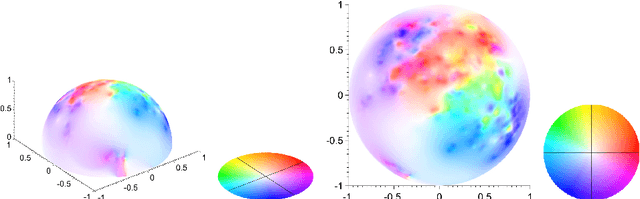
We propose a number of variational regularisation methods for the estimation and decomposition of motion fields on the $2$-sphere. While motion estimation is based on the optical flow equation, the presented decomposition models are motivated by recent trends in image analysis. In particular we treat $u+v$ decomposition as well as hierarchical decomposition. Helmholtz decomposition of motion fields is obtained as a natural by-product of the chosen numerical method based on vector spherical harmonics. All models are tested on time-lapse microscopy data depicting fluorescently labelled endodermal cells of a zebrafish embryo.
* The final publication is available at link.springer.com
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge