From Image Denoisers to Regularizing Imaging Inverse Problems: An Overview

Inverse problems lie at the heart of modern imaging science, with broad applications in areas such as medical imaging, remote sensing, and microscopy. Recent years have witnessed a paradigm shift in solving imaging inverse problems, where data-driven regularizers are used increasingly, leading to remarkably high-fidelity reconstruction. A particularly notable approach for data-driven regularization is to use learned image denoisers as implicit priors in iterative image reconstruction algorithms. This survey presents a comprehensive overview of this powerful and emerging class of algorithms, commonly referred to as plug-and-play (PnP) methods. We begin by providing a brief background on image denoising and inverse problems, followed by a short review of traditional regularization strategies. We then explore how proximal splitting algorithms, such as the alternating direction method of multipliers (ADMM) and proximal gradient descent (PGD), can naturally accommodate learned denoisers in place of proximal operators, and under what conditions such replacements preserve convergence. The role of Tweedie's formula in connecting optimal Gaussian denoisers and score estimation is discussed, which lays the foundation for regularization-by-denoising (RED) and more recent diffusion-based posterior sampling methods. We discuss theoretical advances regarding the convergence of PnP algorithms, both within the RED and proximal settings, emphasizing the structural assumptions that the denoiser must satisfy for convergence, such as non-expansiveness, Lipschitz continuity, and local homogeneity. We also address practical considerations in algorithm design, including choices of denoiser architecture and acceleration strategies.

Dataset Distillation as Pushforward Optimal Quantization

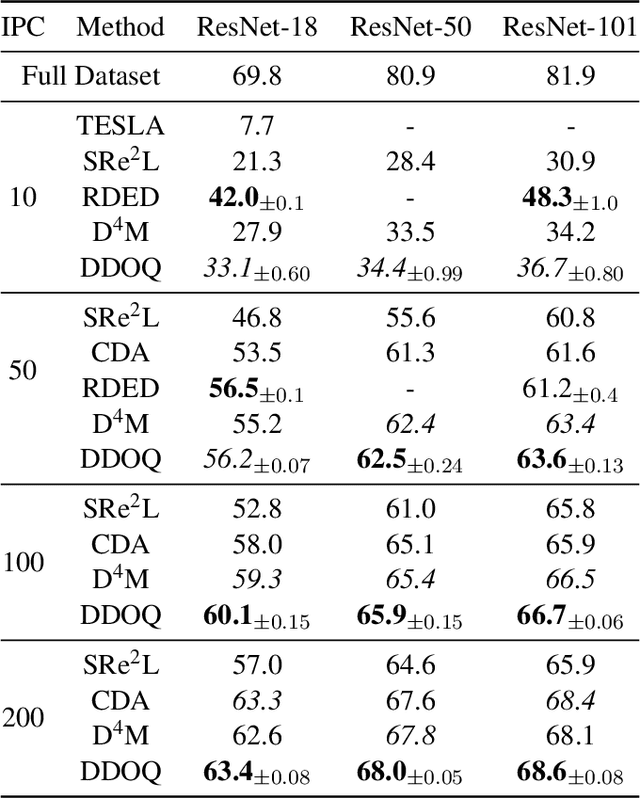
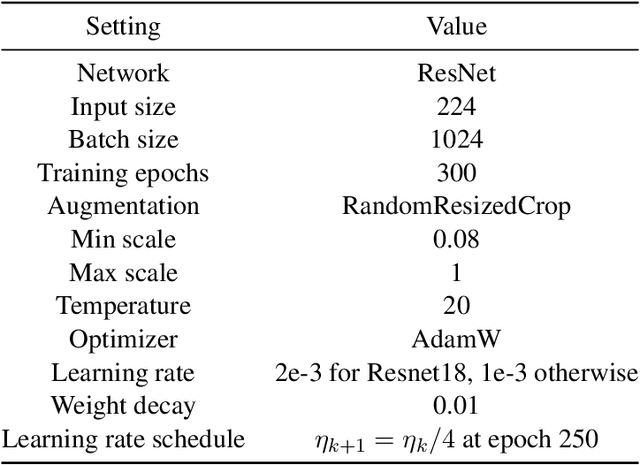
Dataset distillation aims to find a synthetic training set such that training on the synthetic data achieves similar performance to training on real data, with orders of magnitude less computational requirements. Existing methods can be broadly categorized as either bi-level optimization problems that have neural network training heuristics as the lower level problem, or disentangled methods that bypass the bi-level optimization by matching distributions of data. The latter method has the major advantages of speed and scalability in terms of size of both training and distilled datasets. We demonstrate that when equipped with an encoder-decoder structure, the empirically successful disentangled methods can be reformulated as an optimal quantization problem, where a finite set of points is found to approximate the underlying probability measure by minimizing the expected projection distance. In particular, we link existing disentangled dataset distillation methods to the classical optimal quantization and Wasserstein barycenter problems, demonstrating consistency of distilled datasets for diffusion-based generative priors. We propose a simple extension of the state-of-the-art data distillation method D4M, achieving better performance on the ImageNet-1K dataset with trivial additional computation, and state-of-the-art performance in higher image-per-class settings.

Blessing of Dimensionality for Approximating Sobolev Classes on Manifolds

The manifold hypothesis says that natural high-dimensional data is actually supported on or around a low-dimensional manifold. Recent success of statistical and learning-based methods empirically supports this hypothesis, due to outperforming classical statistical intuition in very high dimensions. A natural step for analysis is thus to assume the manifold hypothesis and derive bounds that are independent of any embedding space. Theoretical implications in this direction have recently been explored in terms of generalization of ReLU networks and convergence of Langevin methods. We complement existing results by providing theoretical statistical complexity results, which directly relates to generalization properties. In particular, we demonstrate that the statistical complexity required to approximate a class of bounded Sobolev functions on a compact manifold is bounded from below, and moreover that this bound is dependent only on the intrinsic properties of the manifold. These provide complementary bounds for existing approximation results for ReLU networks on manifolds, which give upper bounds on generalization capacity.

Unsupervised Training of Convex Regularizers using Maximum Likelihood Estimation

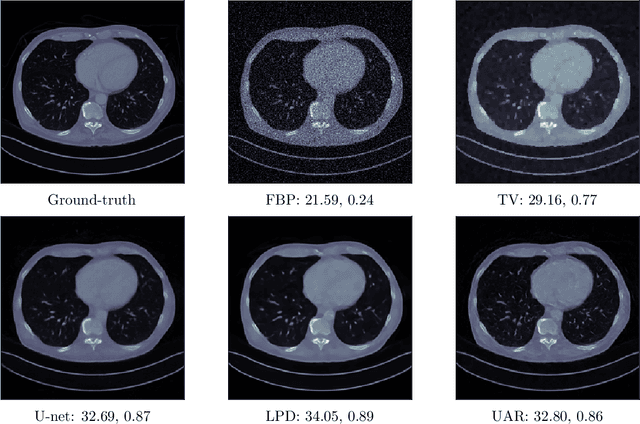
Unsupervised learning is a training approach in the situation where ground truth data is unavailable, such as inverse imaging problems. We present an unsupervised Bayesian training approach to learning convex neural network regularizers using a fixed noisy dataset, based on a dual Markov chain estimation method. Compared to classical supervised adversarial regularization methods, where there is access to both clean images as well as unlimited to noisy copies, we demonstrate close performance on natural image Gaussian deconvolution and Poisson denoising tasks.

Unsupervised approaches based on optimal transport and convex analysis for inverse problems in imaging

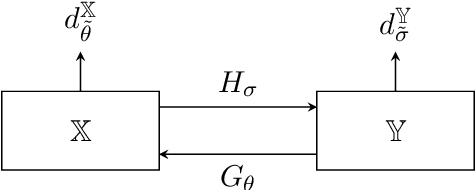
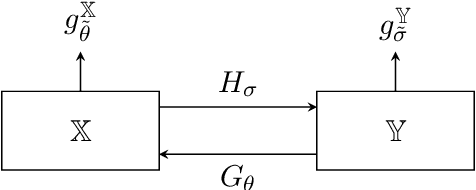
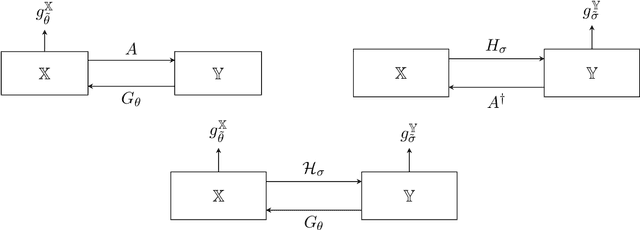
Unsupervised deep learning approaches have recently become one of the crucial research areas in imaging owing to their ability to learn expressive and powerful reconstruction operators even when paired high-quality training data is scarcely available. In this chapter, we review theoretically principled unsupervised learning schemes for solving imaging inverse problems, with a particular focus on methods rooted in optimal transport and convex analysis. We begin by reviewing the optimal transport-based unsupervised approaches such as the cycle-consistency-based models and learned adversarial regularization methods, which have clear probabilistic interpretations. Subsequently, we give an overview of a recent line of works on provably convergent learned optimization algorithms applied to accelerate the solution of imaging inverse problems, alongside their dedicated unsupervised training schemes. We also survey a number of provably convergent plug-and-play algorithms (based on gradient-step deep denoisers), which are among the most important and widely applied unsupervised approaches for imaging problems. At the end of this survey, we provide an overview of a few related unsupervised learning frameworks that complement our focused schemes. Together with a detailed survey, we provide an overview of the key mathematical results that underlie the methods reviewed in the chapter to keep our discussion self-contained.

Noise-Free Sampling Algorithms via Regularized Wasserstein Proximals

We consider the problem of sampling from a distribution governed by a potential function. This work proposes an explicit score-based MCMC method that is deterministic, resulting in a deterministic evolution for particles rather than a stochastic differential equation evolution. The score term is given in closed form by a regularized Wasserstein proximal, using a kernel convolution that is approximated by sampling. We demonstrate fast convergence on various problems and show improved dimensional dependence of mixing time bounds for the case of Gaussian distributions compared to the unadjusted Langevin algorithm (ULA) and the Metropolis-adjusted Langevin algorithm (MALA). We additionally derive closed form expressions for the distributions at each iterate for quadratic potential functions, characterizing the variance reduction. Empirical results demonstrate that the particles behave in an organized manner, lying on level set contours of the potential. Moreover, the posterior mean estimator of the proposed method is shown to be closer to the maximum a-posteriori estimator compared to ULA and MALA, in the context of Bayesian logistic regression.

Provably Convergent Plug-and-Play Quasi-Newton Methods

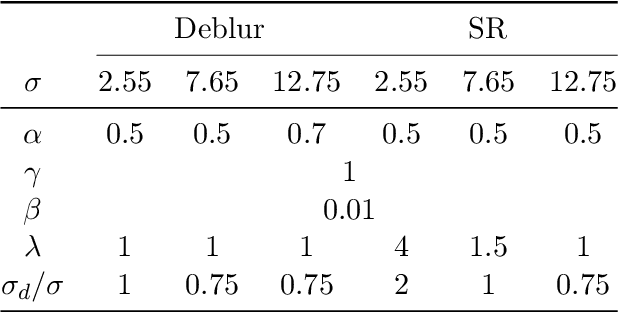
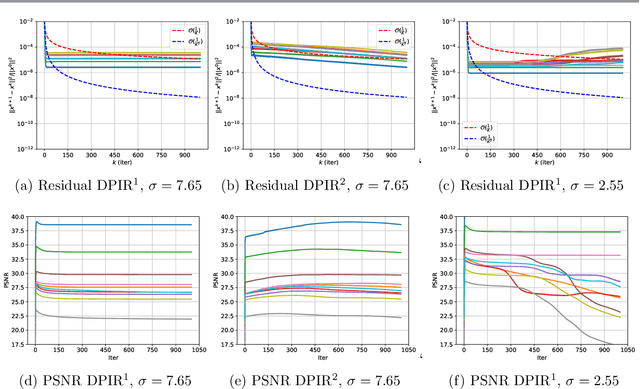
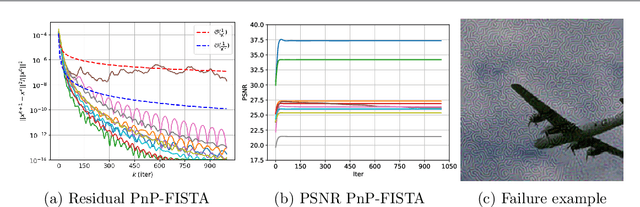
Plug-and-Play (PnP) methods are a class of efficient iterative methods that aim to combine data fidelity terms and deep denoisers using classical optimization algorithms, such as ISTA or ADMM. Existing provable PnP methods impose heavy restrictions on the denoiser or fidelity function, such as nonexpansiveness or strict convexity. In this work, we propose a provable PnP method that imposes relatively light conditions based on proximal denoisers, and introduce a quasi-Newton step to greatly accelerate convergence. By specially parameterizing the deep denoiser as a gradient step, we further characterize the fixed-points of the quasi-Newton PnP algorithm.