Out-of-distribution evaluations of channel agnostic masked autoencoders in fluorescence microscopy

Developing computer vision for high-content screening is challenging due to various sources of distribution-shift caused by changes in experimental conditions, perturbagens, and fluorescent markers. The impact of different sources of distribution-shift are confounded in typical evaluations of models based on transfer learning, which limits interpretations of how changes to model design and training affect generalisation. We propose an evaluation scheme that isolates sources of distribution-shift using the JUMP-CP dataset, allowing researchers to evaluate generalisation with respect to specific sources of distribution-shift. We then present a channel-agnostic masked autoencoder $\mathbf{Campfire}$ which, via a shared decoder for all channels, scales effectively to datasets containing many different fluorescent markers, and show that it generalises to out-of-distribution experimental batches, perturbagens, and fluorescent markers, and also demonstrates successful transfer learning from one cell type to another.

Dataset Distillation as Pushforward Optimal Quantization

Dataset distillation aims to find a synthetic training set such that training on the synthetic data achieves similar performance to training on real data, with orders of magnitude less computational requirements. Existing methods can be broadly categorized as either bi-level optimization problems that have neural network training heuristics as the lower level problem, or disentangled methods that bypass the bi-level optimization by matching distributions of data. The latter method has the major advantages of speed and scalability in terms of size of both training and distilled datasets. We demonstrate that when equipped with an encoder-decoder structure, the empirically successful disentangled methods can be reformulated as an optimal quantization problem, where a finite set of points is found to approximate the underlying probability measure by minimizing the expected projection distance. In particular, we link existing disentangled dataset distillation methods to the classical optimal quantization and Wasserstein barycenter problems, demonstrating consistency of distilled datasets for diffusion-based generative priors. We propose a simple extension of the state-of-the-art data distillation method D4M, achieving better performance on the ImageNet-1K dataset with trivial additional computation, and state-of-the-art performance in higher image-per-class settings.

Self-supervised learning of multi-omics embeddings in the low-label, high-data regime

Contrastive, self-supervised learning (SSL) is used to train a model that predicts cancer type from miRNA, mRNA or RPPA expression data. This model, a pretrained FT-Transformer, is shown to outperform XGBoost and CatBoost, standard benchmarks for tabular data, when labelled samples are scarce but the number of unlabelled samples is high. This is despite the fact that the datasets we use have $\mathcal{O}(10^{1})$ classes and $\mathcal{O}(10^{2})-\mathcal{O}(10^{4})$ features. After demonstrating the efficacy of our chosen method of self-supervised pretraining, we investigate SSL for multi-modal models. A late-fusion model is proposed, where each omics is passed through its own sub-network, the outputs of which are averaged and passed to the pretraining or downstream objective function. Multi-modal pretraining is shown to improve predictions from a single omics, and we argue that this is useful for datasets with many unlabelled multi-modal samples, but few labelled unimodal samples. Additionally, we show that pretraining each omics-specific module individually is highly effective. This enables the application of the proposed model in a variety of contexts where a large amount of unlabelled data is available from each omics, but only a few labelled samples.

Mining of Single-Class by Active Learning for Semantic Segmentation

Several Active Learning (AL) policies require retraining a target model several times in order to identify the most informative samples and rarely offer the option to focus on the acquisition of samples from underrepresented classes. Here the Mining of Single-Class by Active Learning (MiSiCAL) paradigm is introduced where an AL policy is constructed through deep reinforcement learning and exploits quantity-accuracy correlations to build datasets on which high-performance models can be trained with regards to specific classes. MiSiCAL is especially helpful in the case of very large batch sizes since it does not require repeated model training sessions as is common in other AL methods. This is thanks to its ability to exploit fixed representations of the candidate data points. We find that MiSiCAL is able to outperform a random policy on 150 out of 171 COCO10k classes, while the strongest baseline only outperforms random on 101 classes.

Deep reinforced active learning for multi-class image classification

High accuracy medical image classification can be limited by the costs of acquiring more data as well as the time and expertise needed to label existing images. In this paper, we apply active learning to medical image classification, a method which aims to maximise model performance on a minimal subset from a larger pool of data. We present a new active learning framework, based on deep reinforcement learning, to learn an active learning query strategy to label images based on predictions from a convolutional neural network. Our framework modifies the deep-Q network formulation, allowing us to pick data based additionally on geometric arguments in the latent space of the classifier, allowing for high accuracy multi-class classification in a batch-based active learning setting, enabling the agent to label datapoints that are both diverse and about which it is most uncertain. We apply our framework to two medical imaging datasets and compare with standard query strategies as well as the most recent reinforcement learning based active learning approach for image classification.

GNisi: A graph network for reconstructing Ising models from multivariate binarized data

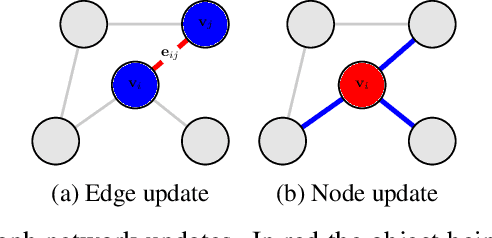
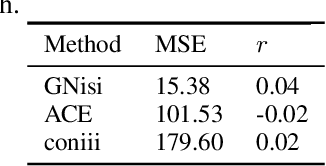
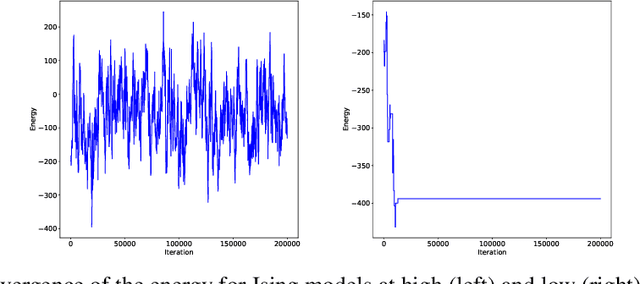
Ising models are a simple generative approach to describing interacting binary variables. They have proven useful in a number of biological settings because they enable one to represent observed many-body correlations as the separable consequence of many direct, pairwise statistical interactions. The inference of Ising models from data can be computationally very challenging and often one must be satisfied with numerical approximations or limited precision. In this paper we present a novel method for the determination of Ising parameters from data, called GNisi, which uses a Graph Neural network trained on known Ising models in order to construct the parameters for unseen data. We show that GNisi is more accurate than the existing state of the art software, and we illustrate our method by applying GNisi to gene expression data.

Data efficiency in graph networks through equivariance

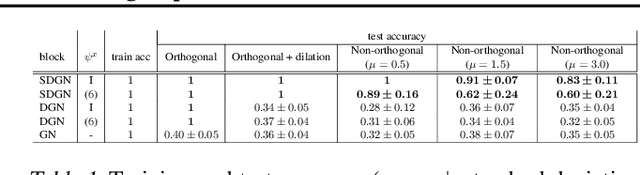
We introduce a novel architecture for graph networks which is equivariant to any transformation in the coordinate embeddings that preserves the distance between neighbouring nodes. In particular, it is equivariant to the Euclidean and conformal orthogonal groups in $n$-dimensions. Thanks to its equivariance properties, the proposed model is extremely more data efficient with respect to classical graph architectures and also intrinsically equipped with a better inductive bias. We show that, learning on a minimal amount of data, the architecture we propose can perfectly generalise to unseen data in a synthetic problem, while much more training data are required from a standard model to reach comparable performance.

Symmetry-driven graph neural networks

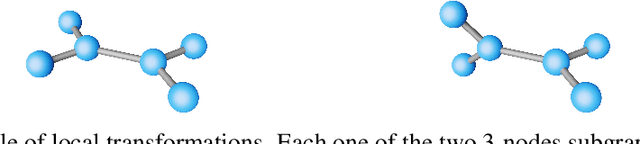
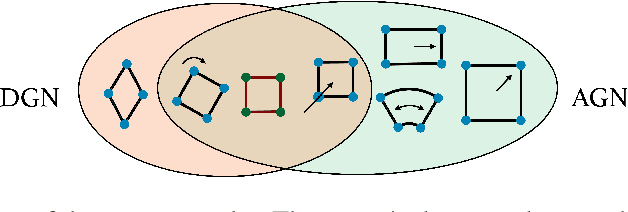
Exploiting symmetries and invariance in data is a powerful, yet not fully exploited, way to achieve better generalisation with more efficiency. In this paper, we introduce two graph network architectures that are equivariant to several types of transformations affecting the node coordinates. First, we build equivariance to any transformation in the coordinate embeddings that preserves the distance between neighbouring nodes, allowing for equivariance to the Euclidean group. Then, we introduce angle attributes to build equivariance to any angle preserving transformation - thus, to the conformal group. Thanks to their equivariance properties, the proposed models can be vastly more data efficient with respect to classical graph architectures, intrinsically equipped with a better inductive bias and better at generalising. We demonstrate these capabilities on a synthetic dataset composed of $n$-dimensional geometric objects. Additionally, we provide examples of their limitations when (the right) symmetries are not present in the data.

Beyond permutation equivariance in graph networks

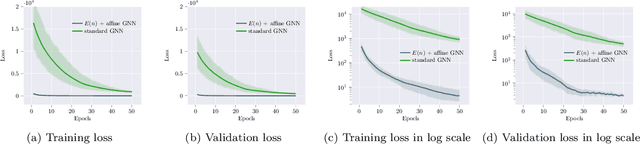
We introduce a novel architecture for graph networks which is equivariant to the Euclidean group in $n$-dimensions, and is additionally able to deal with affine transformations. Our model is designed to work with graph networks in their most general form, thus including particular variants as special cases. Thanks to its equivariance properties, we expect the proposed model to be more data efficient with respect to classical graph architectures and also intrinsically equipped with a better inductive bias. As a preliminary example, we show that the architecture with both equivariance under the Euclidean group, as well as the affine transformations, performs best on a standard dataset for graph neural networks.