Beyond permutation equivariance in graph networks
Paper and Code
Mar 30, 2021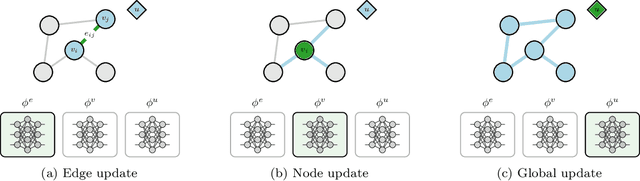
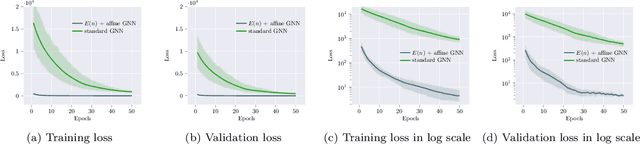
We introduce a novel architecture for graph networks which is equivariant to the Euclidean group in $n$-dimensions, and is additionally able to deal with affine transformations. Our model is designed to work with graph networks in their most general form, thus including particular variants as special cases. Thanks to its equivariance properties, we expect the proposed model to be more data efficient with respect to classical graph architectures and also intrinsically equipped with a better inductive bias. As a preliminary example, we show that the architecture with both equivariance under the Euclidean group, as well as the affine transformations, performs best on a standard dataset for graph neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge