Data efficiency in graph networks through equivariance

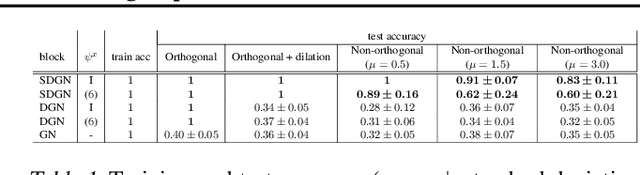
We introduce a novel architecture for graph networks which is equivariant to any transformation in the coordinate embeddings that preserves the distance between neighbouring nodes. In particular, it is equivariant to the Euclidean and conformal orthogonal groups in $n$-dimensions. Thanks to its equivariance properties, the proposed model is extremely more data efficient with respect to classical graph architectures and also intrinsically equipped with a better inductive bias. We show that, learning on a minimal amount of data, the architecture we propose can perfectly generalise to unseen data in a synthetic problem, while much more training data are required from a standard model to reach comparable performance.

Intrinsic uncertainties and where to find them

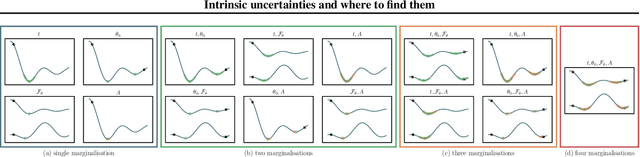
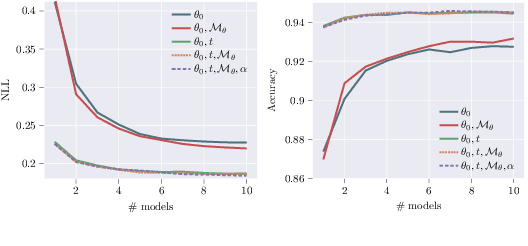
We introduce a framework for uncertainty estimation that both describes and extends many existing methods. We consider typical hyperparameters involved in classical training as random variables and marginalise them out to capture various sources of uncertainty in the parameter space. We investigate which forms and combinations of marginalisation are most useful from a practical point of view on standard benchmarking data sets. Moreover, we discuss how some marginalisations may produce reliable estimates of uncertainty without the need for extensive hyperparameter tuning and/or large-scale ensembling.

Symmetry-driven graph neural networks

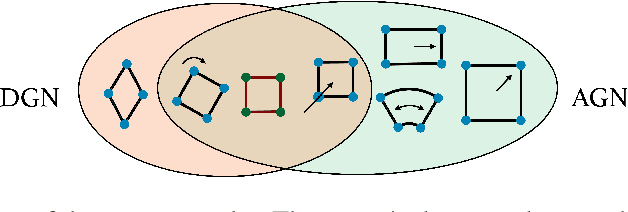
Exploiting symmetries and invariance in data is a powerful, yet not fully exploited, way to achieve better generalisation with more efficiency. In this paper, we introduce two graph network architectures that are equivariant to several types of transformations affecting the node coordinates. First, we build equivariance to any transformation in the coordinate embeddings that preserves the distance between neighbouring nodes, allowing for equivariance to the Euclidean group. Then, we introduce angle attributes to build equivariance to any angle preserving transformation - thus, to the conformal group. Thanks to their equivariance properties, the proposed models can be vastly more data efficient with respect to classical graph architectures, intrinsically equipped with a better inductive bias and better at generalising. We demonstrate these capabilities on a synthetic dataset composed of $n$-dimensional geometric objects. Additionally, we provide examples of their limitations when (the right) symmetries are not present in the data.

Beyond permutation equivariance in graph networks

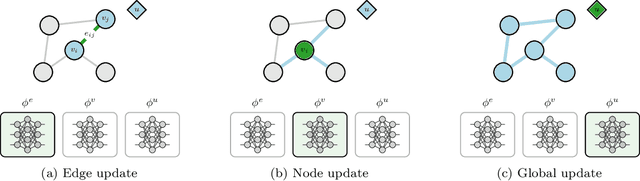
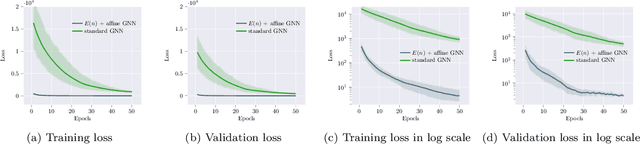
We introduce a novel architecture for graph networks which is equivariant to the Euclidean group in $n$-dimensions, and is additionally able to deal with affine transformations. Our model is designed to work with graph networks in their most general form, thus including particular variants as special cases. Thanks to its equivariance properties, we expect the proposed model to be more data efficient with respect to classical graph architectures and also intrinsically equipped with a better inductive bias. As a preliminary example, we show that the architecture with both equivariance under the Euclidean group, as well as the affine transformations, performs best on a standard dataset for graph neural networks.

Distributed Online Optimization via Gradient Tracking with Adaptive Momentum

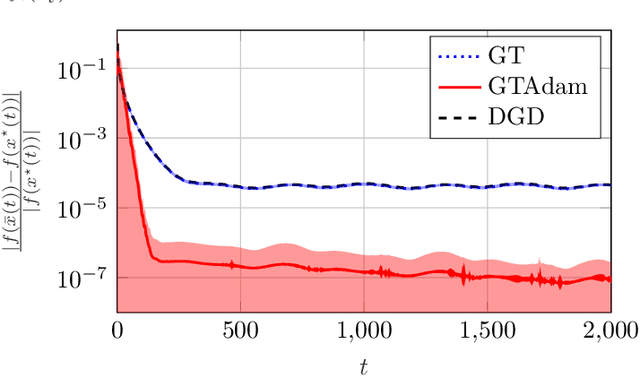
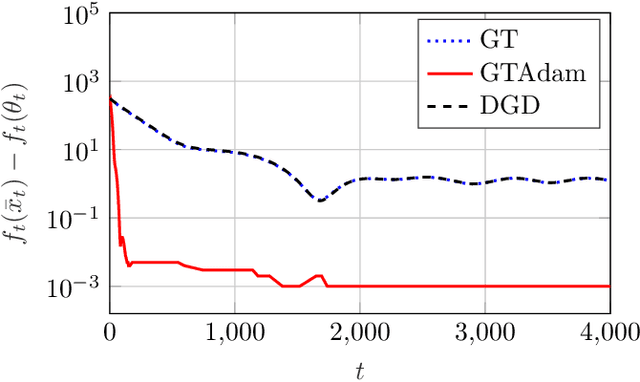
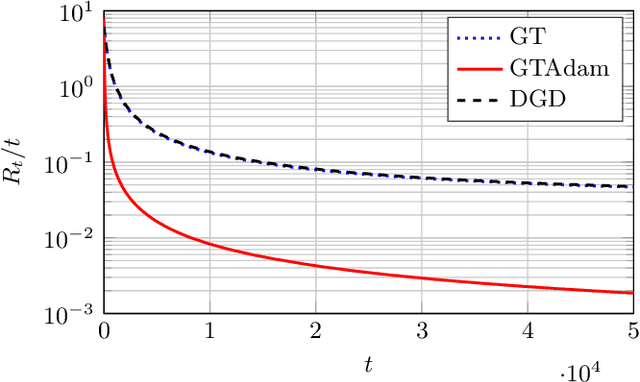
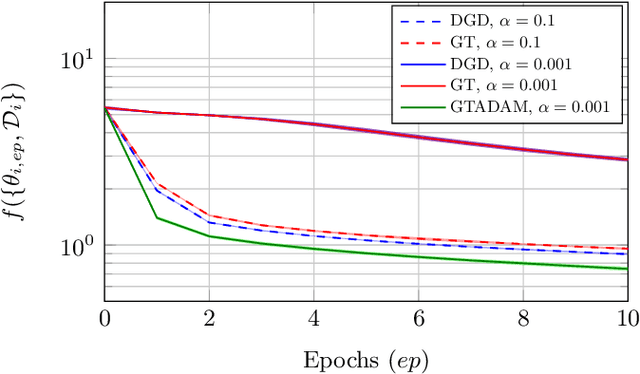
This paper deals with a network of computing agents aiming to solve an online optimization problem in a distributed fashion, i.e., by means of local computation and communication, without any central coordinator. We propose the gradient tracking with adaptive momentum estimation (GTAdam) distributed algorithm, which combines a gradient tracking mechanism with first and second order momentum estimates of the gradient. The algorithm is analyzed in the online setting for strongly convex and smooth cost functions. We prove that the average dynamic regret is bounded and that the convergence rate is linear. The algorithm is tested on a time-varying classification problem, on a (moving) target localization problem and in a stochastic optimization setup from image classification. In these numerical experiments from multi-agent learning, GTAdam outperforms state-of-the-art distributed optimization methods.

Collective Learning

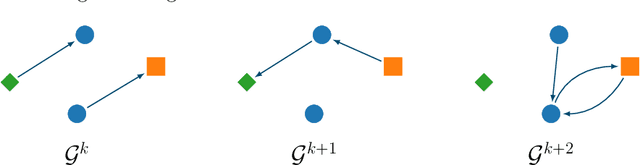
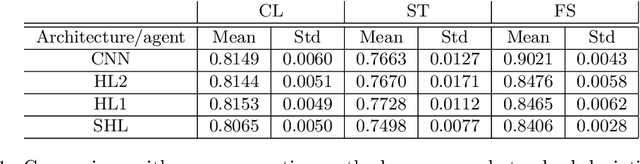
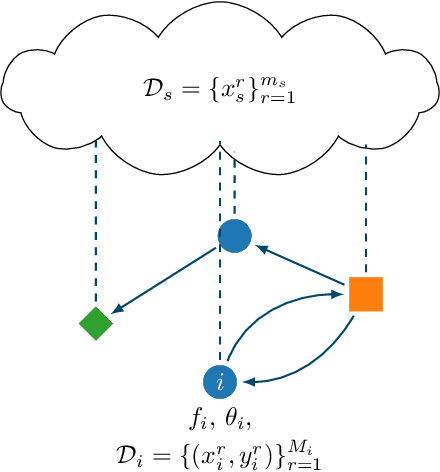
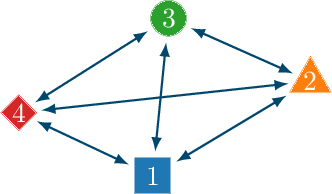
In this paper, we introduce the concept of collective learning (CL) which exploits the notion of collective intelligence in the field of distributed semi-supervised learning. The proposed framework draws inspiration from the learning behavior of human beings, who alternate phases involving collaboration, confrontation and exchange of views with other consisting of studying and learning on their own. On this regard, CL comprises two main phases: a self-training phase in which learning is performed on local private (labeled) data only and a collective training phase in which proxy-labels are assigned to shared (unlabeled) data by means of a consensus-based algorithm. In the considered framework, heterogeneous systems can be connected over the same network, each with different computational capabilities and resources and everyone in the network may take advantage of the cooperation and will eventually reach higher performance with respect to those it can reach on its own. An extensive experimental campaign on an image classification problem emphasizes the properties of CL by analyzing the performance achieved by the cooperating agents.

Asynchronous Distributed Learning from Constraints

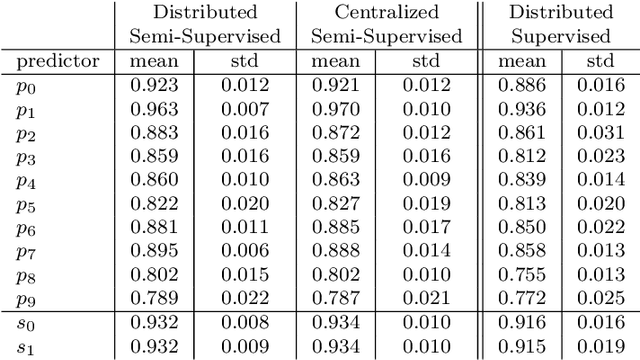
In this paper, the extension of the framework of Learning from Constraints (LfC) to a distributed setting where multiple parties, connected over the network, contribute to the learning process is studied. LfC relies on the generic notion of "constraint" to inject knowledge into the learning problem and, due to its generality, it deals with possibly nonconvex constraints, enforced either in a hard or soft way. Motivated by recent progresses in the field of distributed and constrained nonconvex optimization, we apply the (distributed) Asynchronous Method of Multipliers (ASYMM) to LfC. The study shows that such a method allows us to support scenarios where selected constraints (i.e., knowledge), data, and outcomes of the learning process can be locally stored in each computational node without being shared with the rest of the network, opening the road to further investigations into privacy-preserving LfC. Constraints act as a bridge between what is shared over the net and what is private to each node and no central authority is required. We demonstrate the applicability of these ideas in two distributed real-world settings in the context of digit recognition and document classification.

Upper Body Pose Estimation Using Wearable Inertial Sensors and Multiplicative Kalman Filter

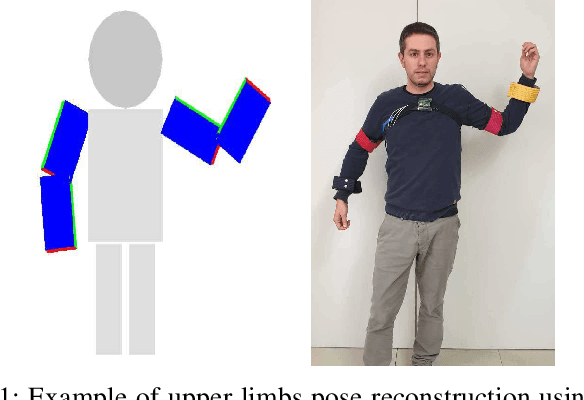
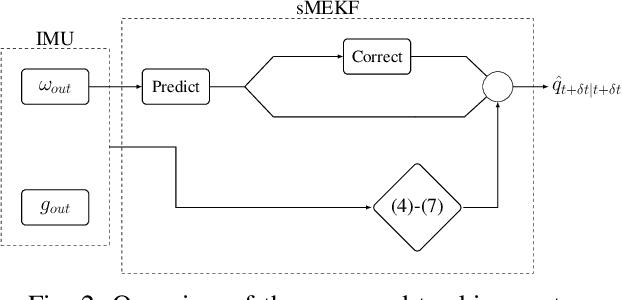
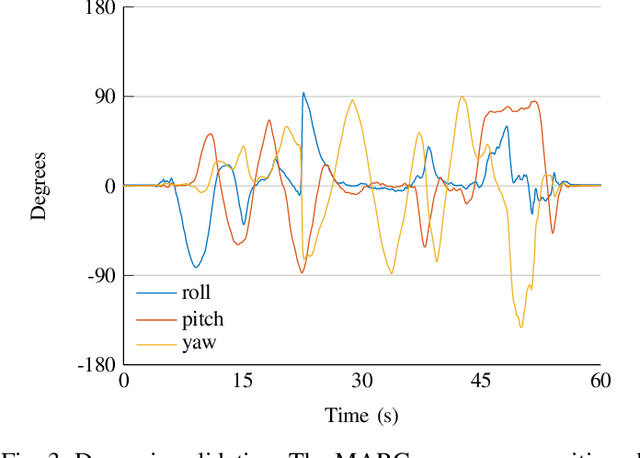
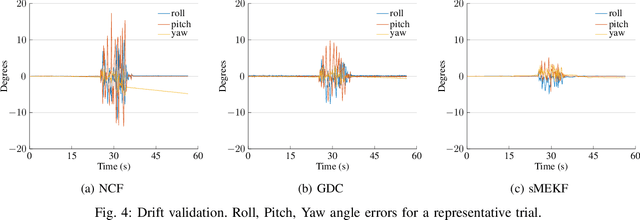
Estimating the limbs pose in a wearable way may benefit multiple areas such as rehabilitation, teleoperation, human-robot interaction, gaming, and many more. Several solutions are commercially available, but they are usually expensive or not wearable/portable. We present a wearable pose estimation system (WePosE), based on inertial measurements units (IMUs), for motion analysis and body tracking. Differently from camera-based approaches, the proposed system does not suffer from occlusion problems and lighting conditions, it is cost effective and it can be used in indoor and outdoor environments. Moreover, since only accelerometers and gyroscopes are used to estimate the orientation, the system can be used also in the presence of iron and magnetic disturbances. An experimental validation using a high precision optical tracker has been performed. Results confirmed the effectiveness of the proposed approach.

Distributed Submodular Minimization via Block-Wise Updates and Communications

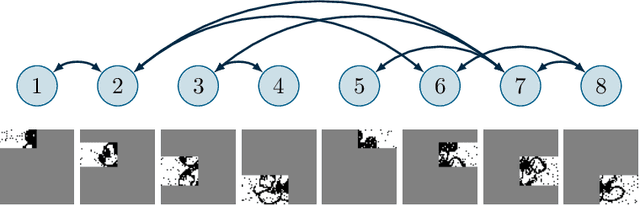
In this paper we deal with a network of computing agents with local processing and neighboring communication capabilities that aim at solving (without any central unit) a submodular optimization problem. The cost function is the sum of many local submodular functions and each agent in the network has access to one function in the sum only. In this \emph{distributed} set-up, in order to preserve their own privacy, agents communicate with neighbors but do not share their local cost functions. We propose a distributed algorithm in which agents resort to the Lov\`{a}sz extension of their local submodular functions and perform local updates and communications in terms of single blocks of the entire optimization variable. Updates are performed by means of a greedy algorithm which is run only until the selected block is computed, thus resulting in a reduced computational burden. The proposed algorithm is shown to converge in expected value to the optimal cost of the problem, and an approximate solution to the submodular problem is retrieved by a thresholding operation. As an application, we consider a distributed image segmentation problem in which each agent has access only to a portion of the entire image. While agent cannot segment the entire image on their own, they correctly complete the task by cooperating through the proposed distributed algorithm.