Andrea Testa
Contact Wasserstein Geodesics for Non-Conservative Schrödinger Bridges
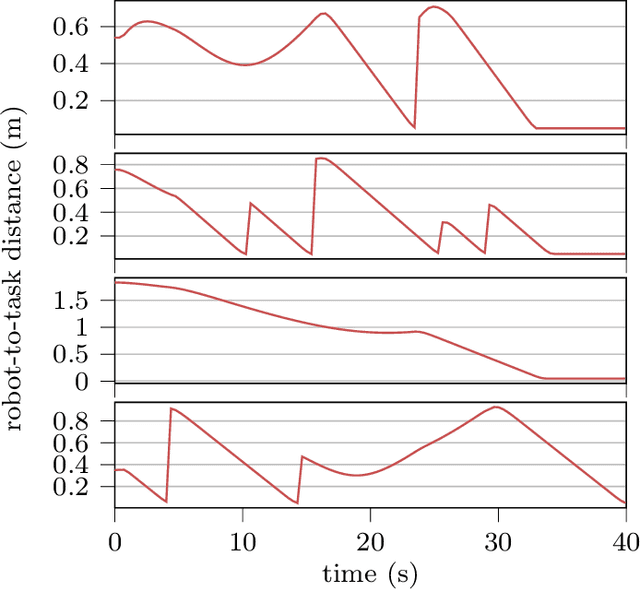
Nov 11, 2025Abstract:The Schrödinger Bridge provides a principled framework for modeling stochastic processes between distributions; however, existing methods are limited by energy-conservation assumptions, which constrains the bridge's shape preventing it from model varying-energy phenomena. To overcome this, we introduce the non-conservative generalized Schrödinger bridge (NCGSB), a novel, energy-varying reformulation based on contact Hamiltonian mechanics. By allowing energy to change over time, the NCGSB provides a broader class of real-world stochastic processes, capturing richer and more faithful intermediate dynamics. By parameterizing the Wasserstein manifold, we lift the bridge problem to a tractable geodesic computation in a finite-dimensional space. Unlike computationally expensive iterative solutions, our contact Wasserstein geodesic (CWG) is naturally implemented via a ResNet architecture and relies on a non-iterative solver with near-linear complexity. Furthermore, CWG supports guided generation by modulating a task-specific distance metric. We validate our framework on tasks including manifold navigation, molecular dynamics predictions, and image generation, demonstrating its practical benefits and versatility.
A Tutorial on Distributed Optimization for Cooperative Robotics: from Setups and Algorithms to Toolboxes and Research Directions
Sep 08, 2023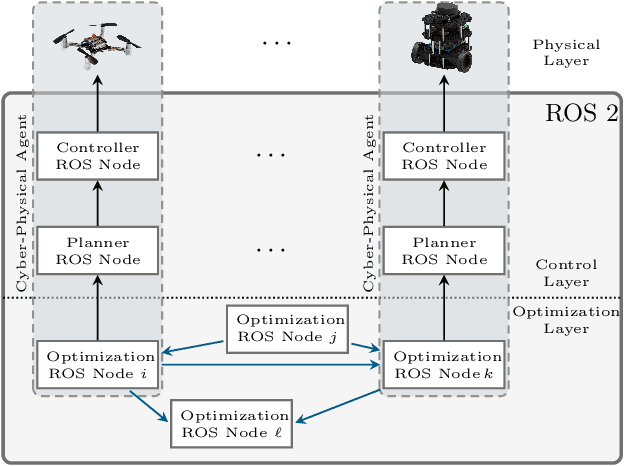
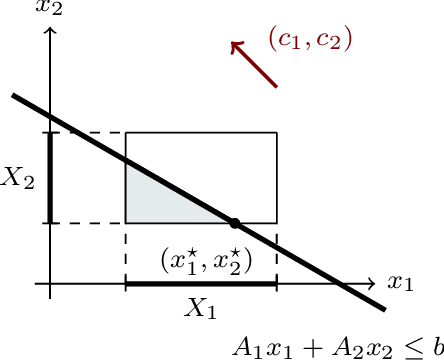
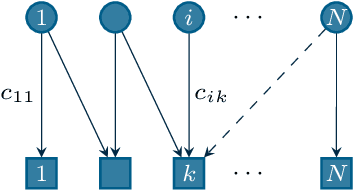
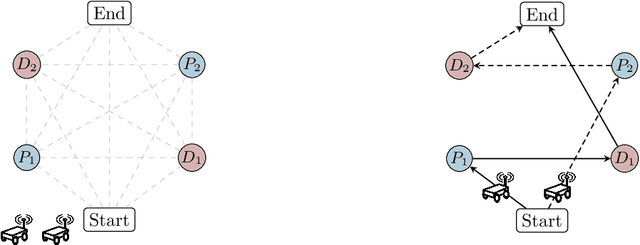
Abstract:Several interesting problems in multi-robot systems can be cast in the framework of distributed optimization. Examples include multi-robot task allocation, vehicle routing, target protection and surveillance. While the theoretical analysis of distributed optimization algorithms has received significant attention, its application to cooperative robotics has not been investigated in detail. In this paper, we show how notable scenarios in cooperative robotics can be addressed by suitable distributed optimization setups. Specifically, after a brief introduction on the widely investigated consensus optimization (most suited for data analytics) and on the partition-based setup (matching the graph structure in the optimization), we focus on two distributed settings modeling several scenarios in cooperative robotics, i.e., the so-called constraint-coupled and aggregative optimization frameworks. For each one, we consider use-case applications, and we discuss tailored distributed algorithms with their convergence properties. Then, we revise state-of-the-art toolboxes allowing for the implementation of distributed schemes on real networks of robots without central coordinators. For each use case, we discuss their implementation in these toolboxes and provide simulations and real experiments on networks of heterogeneous robots.
A Distributed Online Optimization Strategy for Cooperative Robotic Surveillance
Apr 27, 2023



Abstract:In this paper, we propose a distributed algorithm to control a team of cooperating robots aiming to protect a target from a set of intruders. Specifically, we model the strategy of the defending team by means of an online optimization problem inspired by the emerging distributed aggregative framework. In particular, each defending robot determines its own position depending on (i) the relative position between an associated intruder and the target, (ii) its contribution to the barycenter of the team, and (iii) collisions to avoid with its teammates. We highlight that each agent is only aware of local, noisy measurements about the location of the associated intruder and the target. Thus, in each robot, our algorithm needs to (i) locally reconstruct global unavailable quantities and (ii) predict its current objective functions starting from the local measurements. The effectiveness of the proposed methodology is corroborated by simulations and experiments on a team of cooperating quadrotors.
CrazyChoir: Flying Swarms of Crazyflie Quadrotors in ROS 2
Feb 01, 2023
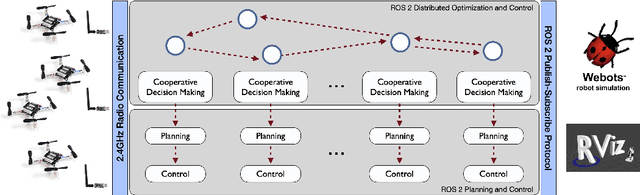
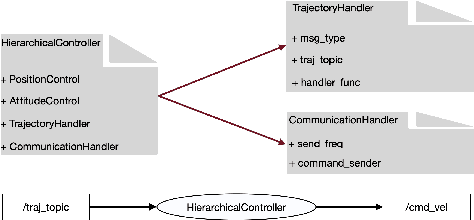
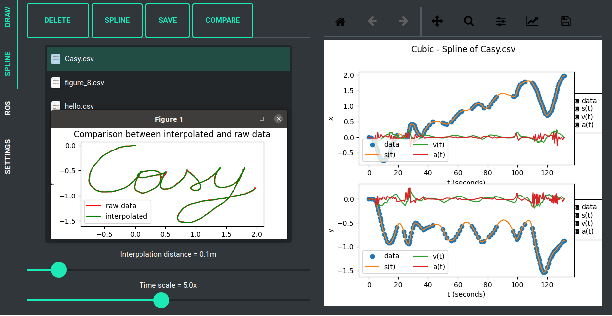
Abstract:This paper introduces CrazyChoir, a modular Python framework based on the Robot Operating System (ROS) 2. The toolbox provides a comprehensive set of functionalities to simulate and run experiments on teams of cooperating Crazyflie nano-quadrotors. Specifically, it allows users to perform realistic simulations over robotic simulators as, e.g., Webots and includes bindings of the firmware control and planning functions. The toolbox also provides libraries to perform radio communication with Crazyflie directly inside ROS 2 scripts. The package can be thus used to design, implement and test planning strategies and control schemes for a Crazyflie nano-quadrotor. Moreover, the modular structure of CrazyChoir allows users to easily implement online distributed optimization and control schemes over multiple quadrotors. The CrazyChoir package is validated via simulations and experiments on a swarm of Crazyflies for formation control, pickup-and-delivery vehicle routing and trajectory tracking tasks. CrazyChoir is available at https://github.com/OPT4SMART/crazychoir.
Multi-Robot Pickup and Delivery via Distributed Resource Allocation
Apr 06, 2021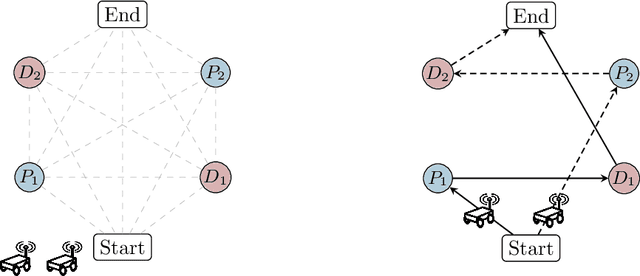
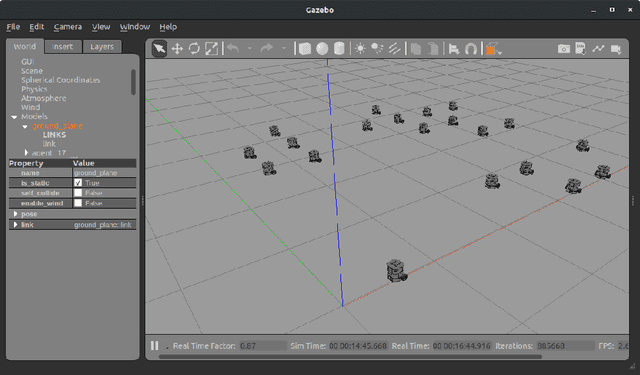

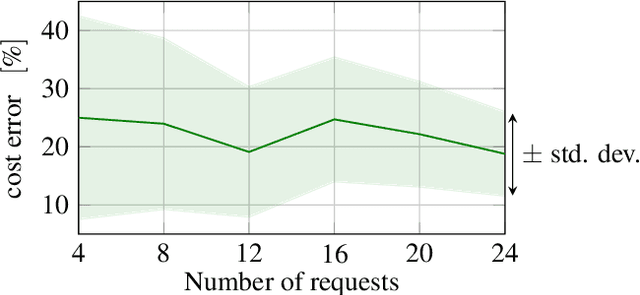
Abstract:In this paper, we consider a large-scale instance of the classical Pickup-and-Delivery Vehicle Routing Problem (PDVRP) that must be solved by a network of mobile cooperating robots. Robots must self-coordinate and self-allocate a set of pickup/delivery tasks while minimizing a given cost figure. This results in a large, challenging Mixed-Integer Linear Problem that must be cooperatively solved without a central coordinator. We propose a distributed algorithm based on a primal decomposition approach that provides a feasible solution to the problem in finite time. An interesting feature of the proposed scheme is that each robot computes only its portion of solution, thereby preserving privacy of sensible information. The algorithm also exhibits attractive scalability properties that guarantee solvability of the problem even in large networks. To the best of our knowledge, this is the first attempt to provide a scalable distributed solution to the problem. The algorithm is first tested through Gazebo simulations on a ROS 2 platform, highlighting the effectiveness of the proposed solution. Finally, experiments on a real testbed with a team of ground and aerial robots are provided.
ChoiRbot: A ROS 2 Toolbox for Cooperative Robotics
Oct 26, 2020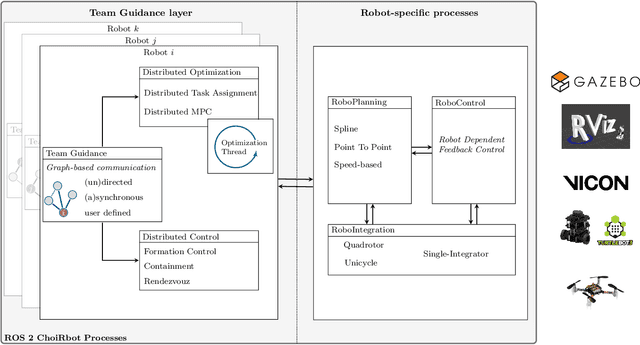

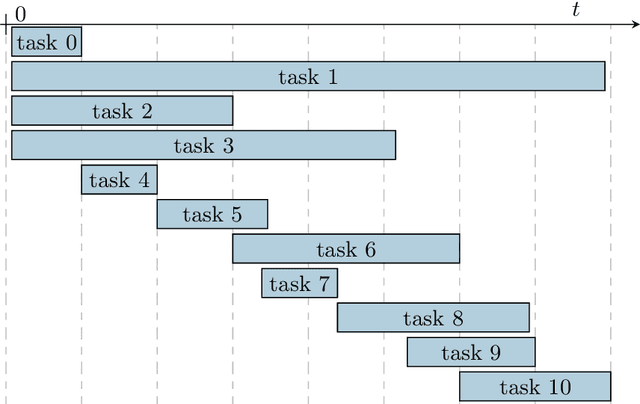
Abstract:In this paper, we introduce ChoiRbot, a toolbox for distributed cooperative robotics based on the novel Robot Operating System (ROS) 2. ChoiRbot provides a fully-functional toolset to execute complex distributed multi-robot tasks, either in simulation or experimentally, with a particular focus on networks of heterogeneous robots without a central coordinator. Thanks to its modular structure, ChoiRbot allows for a highly straight implementation of optimization-based distributed control schemes, such as distributed optimal control, model predictive control, task assignment, in which local computation and communication with neighboring robots are alternated. To this end, the toolbox provides functionalities for the solution of distributed optimization problems. The package can be also used to implement distributed feedback laws that do not need optimization features but do require the exchange of information among robots. The potential of the toolbox is illustrated with simulations and experiments on distributed robotics scenarios with mobile ground robots. The ChoiRbot toolbox is available at https://github.com/OPT4SMART/choirbot.
Distributed Submodular Minimization via Block-Wise Updates and Communications
May 31, 2019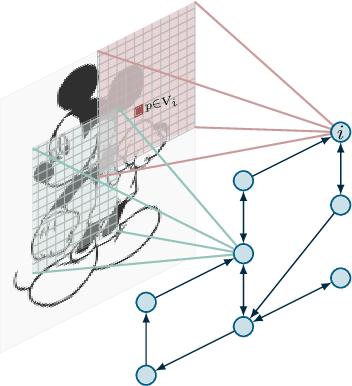
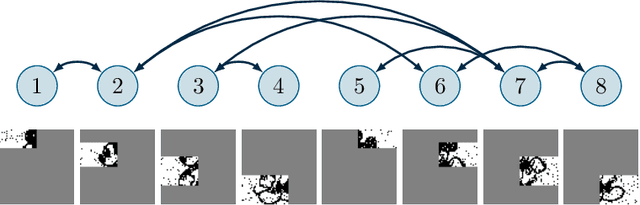

Abstract:In this paper we deal with a network of computing agents with local processing and neighboring communication capabilities that aim at solving (without any central unit) a submodular optimization problem. The cost function is the sum of many local submodular functions and each agent in the network has access to one function in the sum only. In this \emph{distributed} set-up, in order to preserve their own privacy, agents communicate with neighbors but do not share their local cost functions. We propose a distributed algorithm in which agents resort to the Lov\`{a}sz extension of their local submodular functions and perform local updates and communications in terms of single blocks of the entire optimization variable. Updates are performed by means of a greedy algorithm which is run only until the selected block is computed, thus resulting in a reduced computational burden. The proposed algorithm is shown to converge in expected value to the optimal cost of the problem, and an approximate solution to the submodular problem is retrieved by a thresholding operation. As an application, we consider a distributed image segmentation problem in which each agent has access only to a portion of the entire image. While agent cannot segment the entire image on their own, they correctly complete the task by cooperating through the proposed distributed algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge