Accumulator-Aware Post-Training Quantization

Several recent studies have investigated low-precision accumulation, reporting improvements in throughput, power, and area across various platforms. However, the accompanying proposals have only considered the quantization-aware training (QAT) paradigm, in which models are fine-tuned or trained from scratch with quantization in the loop. As models continue to grow in size, QAT techniques become increasingly more expensive, which has motivated the recent surge in post-training quantization (PTQ) research. To the best of our knowledge, ours marks the first formal study of accumulator-aware quantization in the PTQ setting. To bridge this gap, we introduce AXE, a practical framework of accumulator-aware extensions designed to endow overflow avoidance guarantees to existing layer-wise PTQ algorithms. We theoretically motivate AXE and demonstrate its flexibility by implementing it on top of two state-of-the-art PTQ algorithms: GPFQ and OPTQ. We further generalize AXE to support multi-stage accumulation for the first time, opening the door for full datapath optimization and scaling to large language models (LLMs). We evaluate AXE across image classification and language generation models, and observe significant improvements in the trade-off between accumulator bit width and model accuracy over baseline methods.

SPFQ: A Stochastic Algorithm and Its Error Analysis for Neural Network Quantization

Quantization is a widely used compression method that effectively reduces redundancies in over-parameterized neural networks. However, existing quantization techniques for deep neural networks often lack a comprehensive error analysis due to the presence of non-convex loss functions and nonlinear activations. In this paper, we propose a fast stochastic algorithm for quantizing the weights of fully trained neural networks. Our approach leverages a greedy path-following mechanism in combination with a stochastic quantizer. Its computational complexity scales only linearly with the number of weights in the network, thereby enabling the efficient quantization of large networks. Importantly, we establish, for the first time, full-network error bounds, under an infinite alphabet condition and minimal assumptions on the weights and input data. As an application of this result, we prove that when quantizing a multi-layer network having Gaussian weights, the relative square quantization error exhibits a linear decay as the degree of over-parametrization increases. Furthermore, we demonstrate that it is possible to achieve error bounds equivalent to those obtained in the infinite alphabet case, using on the order of a mere $\log\log N$ bits per weight, where $N$ represents the largest number of neurons in a layer.

Post-training Quantization for Neural Networks with Provable Guarantees

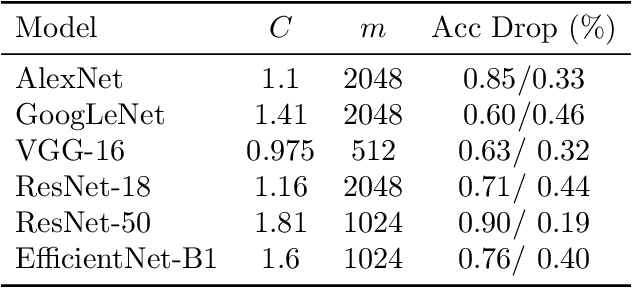
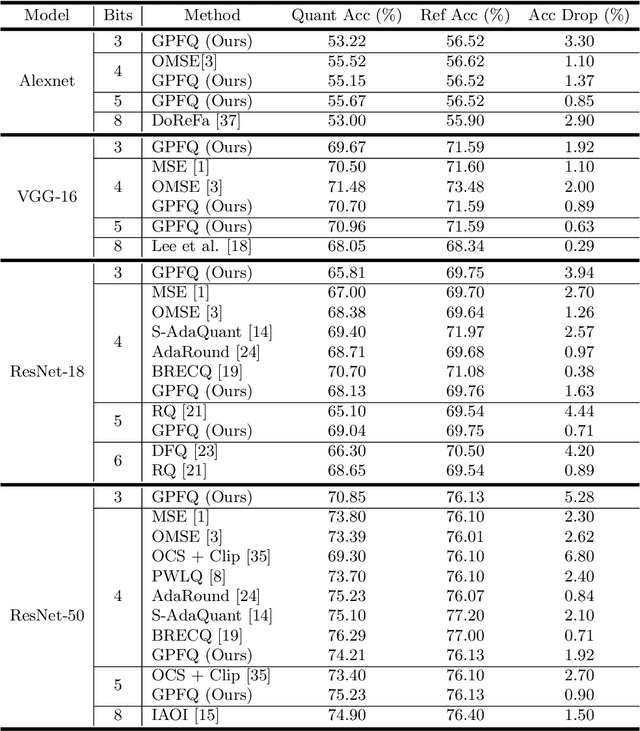
While neural networks have been remarkably successful in a wide array of applications, implementing them in resource-constrained hardware remains an area of intense research. By replacing the weights of a neural network with quantized (e.g., 4-bit, or binary) counterparts, massive savings in computation cost, memory, and power consumption are attained. We modify a post-training neural-network quantization method, GPFQ, that is based on a greedy path-following mechanism, and rigorously analyze its error. We prove that for quantizing a single-layer network, the relative square error essentially decays linearly in the number of weights -- i.e., level of over-parametrization. Our result holds across a range of input distributions and for both fully-connected and convolutional architectures. To empirically evaluate the method, we quantize several common architectures with few bits per weight, and test them on ImageNet, showing only minor loss of accuracy. We also demonstrate that standard modifications, such as bias correction and mixed precision quantization, further improve accuracy.

Sigma-Delta and Distributed Noise-Shaping Quantization Methods for Random Fourier Features

We propose the use of low bit-depth Sigma-Delta and distributed noise-shaping methods for quantizing the Random Fourier features (RFFs) associated with shift-invariant kernels. We prove that our quantized RFFs -- even in the case of $1$-bit quantization -- allow a high accuracy approximation of the underlying kernels, and the approximation error decays at least polynomially fast as the dimension of the RFFs increases. We also show that the quantized RFFs can be further compressed, yielding an excellent trade-off between memory use and accuracy. Namely, the approximation error now decays exponentially as a function of the bits used. Moreover, we empirically show by testing the performance of our methods on several machine learning tasks that our method compares favorably to other state of the art quantization methods in this context.

Faster Binary Embeddings for Preserving Euclidean Distances

We propose a fast, distance-preserving, binary embedding algorithm to transform a high-dimensional dataset $\mathcal{T}\subseteq\mathbb{R}^n$ into binary sequences in the cube $\{\pm 1\}^m$. When $\mathcal{T}$ consists of well-spread (i.e., non-sparse) vectors, our embedding method applies a stable noise-shaping quantization scheme to $A x$ where $A\in\mathbb{R}^{m\times n}$ is a sparse Gaussian random matrix. This contrasts with most binary embedding methods, which usually use $x\mapsto \mathrm{sign}(Ax)$ for the embedding. Moreover, we show that Euclidean distances among the elements of $\mathcal{T}$ are approximated by the $\ell_1$ norm on the images of $\{\pm 1\}^m$ under a fast linear transformation. This again contrasts with standard methods, where the Hamming distance is used instead. Our method is both fast and memory efficient, with time complexity $O(m)$ and space complexity $O(m)$. Further, we prove that the method is accurate and its associated error is comparable to that of a continuous valued Johnson-Lindenstrauss embedding plus a quantization error that admits a polynomial decay as the embedding dimension $m$ increases. Thus the length of the binary codes required to achieve a desired accuracy is quite small, and we show it can even be compressed further without compromising the accuracy. To illustrate our results, we test the proposed method on natural images and show that it achieves strong performance.