SEALion: a Framework for Neural Network Inference on Encrypted Data

We present SEALion: an extensible framework for privacy-preserving machine learning with homomorphic encryption. It allows one to learn deep neural networks that can be seamlessly utilized for prediction on encrypted data. The framework consists of two layers: the first is built upon TensorFlow and SEAL and exposes standard algebra and deep learning primitives; the second implements a Keras-like syntax for training and inference with neural networks. Given a required level of security, a user is abstracted from the details of the encoding and the encryption scheme, allowing quick prototyping. We present two applications that exemplifying the extensibility of our proposal, which are also of independent interest: i) improving efficiency of neural network inference by an activity sparsifier and ii) transfer learning by querying a server-side Variational AutoEncoder that can handle encrypted data.

Three Tools for Practical Differential Privacy

Differentially private learning on real-world data poses challenges for standard machine learning practice: privacy guarantees are difficult to interpret, hyperparameter tuning on private data reduces the privacy budget, and ad-hoc privacy attacks are often required to test model privacy. We introduce three tools to make differentially private machine learning more practical: (1) simple sanity checks which can be carried out in a centralized manner before training, (2) an adaptive clipping bound to reduce the effective number of tuneable privacy parameters, and (3) we show that large-batch training improves model performance.

Sinkhorn AutoEncoders

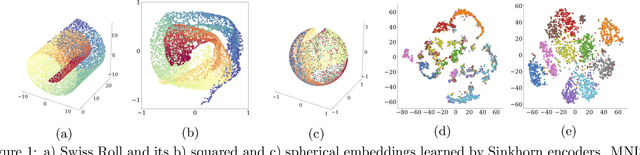
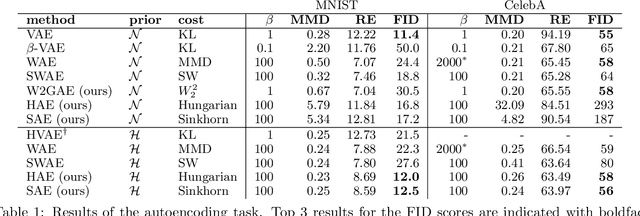
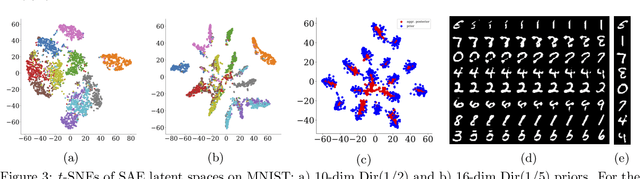
Optimal Transport offers an alternative to maximum likelihood for learning generative autoencoding models. We show how this principle dictates the minimization of the Wasserstein distance between the encoder aggregated posterior and the prior, plus a reconstruction error. We prove that in the non-parametric limit the autoencoder generates the data distribution if and only if the two distributions match exactly, and that the optimum can be obtained by deterministic autoencoders. We then introduce the Sinkhorn AutoEncoder (SAE), which casts the problem into Optimal Transport on the latent space. The resulting Wasserstein distance is minimized by backpropagating through the Sinkhorn algorithm. SAE models the aggregated posterior as an implicit distribution and therefore does not need a reparameterization trick for gradients estimation. Moreover, it requires virtually no adaptation to different prior distributions. We demonstrate its flexibility by considering models with hyperspherical and Dirichlet priors, as well as a simple case of probabilistic programming. SAE matches or outperforms other autoencoding models in visual quality and FID scores.

Entity Resolution and Federated Learning get a Federated Resolution

Consider two data providers, each maintaining records of different feature sets about common entities. They aim to learn a linear model over the whole set of features. This problem of federated learning over vertically partitioned data includes a crucial upstream issue: entity resolution, i.e. finding the correspondence between the rows of the datasets. It is well known that entity resolution, just like learning, is mistake-prone in the real world. Despite the importance of the problem, there has been no formal assessment of how errors in entity resolution impact learning. In this paper, we provide a thorough answer to this question, answering how optimal classifiers, empirical losses, margins and generalisation abilities are affected. While our answer spans a wide set of losses --- going beyond proper, convex, or classification calibrated ---, it brings simple practical arguments to upgrade entity resolution as a preprocessing step to learning. One of these suggests that entity resolution should be aimed at controlling or minimizing the number of matching errors between examples of distinct classes. In our experiments, we modify a simple token-based entity resolution algorithm so that it indeed aims at avoiding matching rows belonging to different classes, and perform experiments in the setting where entity resolution relies on noisy data, which is very relevant to real world domains. Notably, our approach covers the case where one peer \textit{does not} have classes, or a noisy record of classes. Experiments display that using the class information during entity resolution can buy significant uplift for learning at little expense from the complexity standpoint.

Private federated learning on vertically partitioned data via entity resolution and additively homomorphic encryption

Consider two data providers, each maintaining private records of different feature sets about common entities. They aim to learn a linear model jointly in a federated setting, namely, data is local and a shared model is trained from locally computed updates. In contrast with most work on distributed learning, in this scenario (i) data is split vertically, i.e. by features, (ii) only one data provider knows the target variable and (iii) entities are not linked across the data providers. Hence, to the challenge of private learning, we add the potentially negative consequences of mistakes in entity resolution. Our contribution is twofold. First, we describe a three-party end-to-end solution in two phases ---privacy-preserving entity resolution and federated logistic regression over messages encrypted with an additively homomorphic scheme---, secure against a honest-but-curious adversary. The system allows learning without either exposing data in the clear or sharing which entities the data providers have in common. Our implementation is as accurate as a naive non-private solution that brings all data in one place, and scales to problems with millions of entities with hundreds of features. Second, we provide what is to our knowledge the first formal analysis of the impact of entity resolution's mistakes on learning, with results on how optimal classifiers, empirical losses, margins and generalisation abilities are affected. Our results bring a clear and strong support for federated learning: under reasonable assumptions on the number and magnitude of entity resolution's mistakes, it can be extremely beneficial to carry out federated learning in the setting where each peer's data provides a significant uplift to the other.

Making Deep Neural Networks Robust to Label Noise: a Loss Correction Approach

We present a theoretically grounded approach to train deep neural networks, including recurrent networks, subject to class-dependent label noise. We propose two procedures for loss correction that are agnostic to both application domain and network architecture. They simply amount to at most a matrix inversion and multiplication, provided that we know the probability of each class being corrupted into another. We further show how one can estimate these probabilities, adapting a recent technique for noise estimation to the multi-class setting, and thus providing an end-to-end framework. Extensive experiments on MNIST, IMDB, CIFAR-10, CIFAR-100 and a large scale dataset of clothing images employing a diversity of architectures --- stacking dense, convolutional, pooling, dropout, batch normalization, word embedding, LSTM and residual layers --- demonstrate the noise robustness of our proposals. Incidentally, we also prove that, when ReLU is the only non-linearity, the loss curvature is immune to class-dependent label noise.

The Crossover Process: Learnability and Data Protection from Inference Attacks

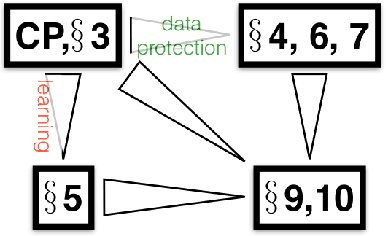
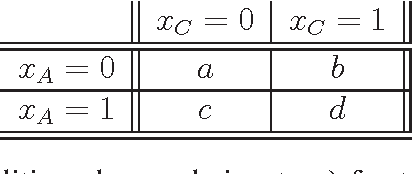
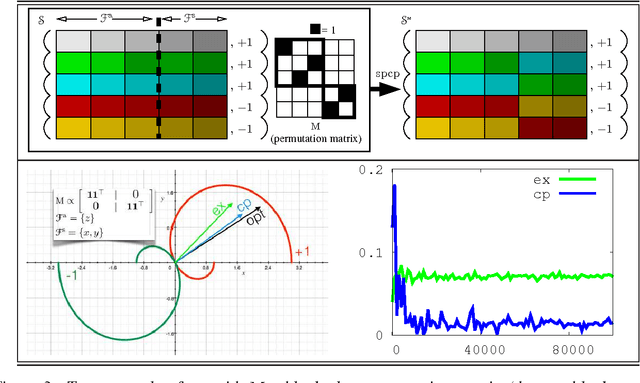
It is usual to consider data protection and learnability as conflicting objectives. This is not always the case: we show how to jointly control inference --- seen as the attack --- and learnability by a noise-free process that mixes training examples, the Crossover Process (cp). One key point is that the cp~is typically able to alter joint distributions without touching on marginals, nor altering the sufficient statistic for the class. In other words, it saves (and sometimes improves) generalization for supervised learning, but can alter the relationship between covariates --- and therefore fool measures of nonlinear independence and causal inference into misleading ad-hoc conclusions. For example, a cp~can increase / decrease odds ratios, bring fairness or break fairness, tamper with disparate impact, strengthen, weaken or reverse causal directions, change observed statistical measures of dependence. For each of these, we quantify changes brought by a cp, as well as its statistical impact on generalization abilities via a new complexity measure that we call the Rademacher cp~complexity. Experiments on a dozen readily available domains validate the theory.

Tsallis Regularized Optimal Transport and Ecological Inference

Optimal transport is a powerful framework for computing distances between probability distributions. We unify the two main approaches to optimal transport, namely Monge-Kantorovitch and Sinkhorn-Cuturi, into what we define as Tsallis regularized optimal transport (\trot). \trot~interpolates a rich family of distortions from Wasserstein to Kullback-Leibler, encompassing as well Pearson, Neyman and Hellinger divergences, to name a few. We show that metric properties known for Sinkhorn-Cuturi generalize to \trot, and provide efficient algorithms for finding the optimal transportation plan with formal convergence proofs. We also present the first application of optimal transport to the problem of ecological inference, that is, the reconstruction of joint distributions from their marginals, a problem of large interest in the social sciences. \trot~provides a convenient framework for ecological inference by allowing to compute the joint distribution --- that is, the optimal transportation plan itself --- when side information is available, which is \textit{e.g.} typically what census represents in political science. Experiments on data from the 2012 US presidential elections display the potential of \trot~in delivering a faithful reconstruction of the joint distribution of ethnic groups and voter preferences.

Fast Learning from Distributed Datasets without Entity Matching

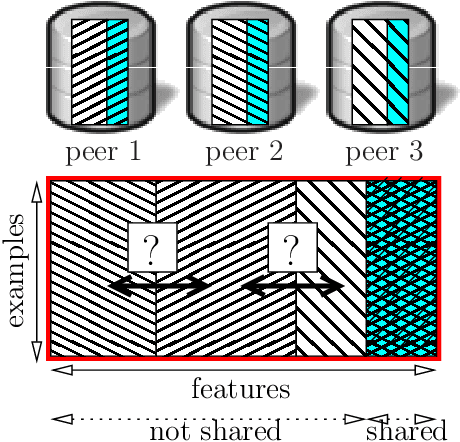
Consider the following data fusion scenario: two datasets/peers contain the same real-world entities described using partially shared features, e.g. banking and insurance company records of the same customer base. Our goal is to learn a classifier in the cross product space of the two domains, in the hard case in which no shared ID is available -- e.g. due to anonymization. Traditionally, the problem is approached by first addressing entity matching and subsequently learning the classifier in a standard manner. We present an end-to-end solution which bypasses matching entities, based on the recently introduced concept of Rademacher observations (rados). Informally, we replace the minimisation of a loss over examples, which requires to solve entity resolution, by the equivalent minimisation of a (different) loss over rados. Among others, key properties we show are (i) a potentially huge subset of these rados does not require to perform entity matching, and (ii) the algorithm that provably minimizes the rado loss over these rados has time and space complexities smaller than the algorithm minimizing the equivalent example loss. Last, we relax a key assumption of the model, that the data is vertically partitioned among peers --- in this case, we would not even know the existence of a solution to entity resolution. In this more general setting, experiments validate the possibility of significantly beating even the optimal peer in hindsight.

Loss factorization, weakly supervised learning and label noise robustness

We prove that the empirical risk of most well-known loss functions factors into a linear term aggregating all labels with a term that is label free, and can further be expressed by sums of the loss. This holds true even for non-smooth, non-convex losses and in any RKHS. The first term is a (kernel) mean operator --the focal quantity of this work-- which we characterize as the sufficient statistic for the labels. The result tightens known generalization bounds and sheds new light on their interpretation. Factorization has a direct application on weakly supervised learning. In particular, we demonstrate that algorithms like SGD and proximal methods can be adapted with minimal effort to handle weak supervision, once the mean operator has been estimated. We apply this idea to learning with asymmetric noisy labels, connecting and extending prior work. Furthermore, we show that most losses enjoy a data-dependent (by the mean operator) form of noise robustness, in contrast with known negative results.