Optimal Grid Layouts for Hybrid Offshore Assets in the North Sea under Different Market Designs

This work examines the Generation and Transmission Expansion (GATE) planning problem of offshore grids under different market clearing mechanisms: a Home Market Design (HMD), a zonal cleared Offshore Bidding Zone (zOBZ) and a nodal cleared Offshore Bidding Zone (nOBZ). It aims at answering two questions. 1) Is knowing the market structure a priori necessary for effective generation and transmission expansion planning? 2) Which market mechanism results in the highest overall social welfare? To this end a multi-period, stochastic GATE planning formulation is developed for both nodal and zonal market designs. The approach considers the costs and benefits among stake-holders of Hybrid Offshore Assets (HOA) as well as gross consumer surplus (GCS). The methodology is demonstrated on a North Sea test grid based on projects from the European Network of Transmission System Operators' (ENTSO-E) Ten Year Network Development Plan (TYNDP). An upper bound on potential social welfare in zonal market designs is calculated and it is concluded that from a generation and transmission perspective, planning under the assumption of an nOBZ results in the best risk adjusted return.

Entity Resolution and Federated Learning get a Federated Resolution

Consider two data providers, each maintaining records of different feature sets about common entities. They aim to learn a linear model over the whole set of features. This problem of federated learning over vertically partitioned data includes a crucial upstream issue: entity resolution, i.e. finding the correspondence between the rows of the datasets. It is well known that entity resolution, just like learning, is mistake-prone in the real world. Despite the importance of the problem, there has been no formal assessment of how errors in entity resolution impact learning. In this paper, we provide a thorough answer to this question, answering how optimal classifiers, empirical losses, margins and generalisation abilities are affected. While our answer spans a wide set of losses --- going beyond proper, convex, or classification calibrated ---, it brings simple practical arguments to upgrade entity resolution as a preprocessing step to learning. One of these suggests that entity resolution should be aimed at controlling or minimizing the number of matching errors between examples of distinct classes. In our experiments, we modify a simple token-based entity resolution algorithm so that it indeed aims at avoiding matching rows belonging to different classes, and perform experiments in the setting where entity resolution relies on noisy data, which is very relevant to real world domains. Notably, our approach covers the case where one peer \textit{does not} have classes, or a noisy record of classes. Experiments display that using the class information during entity resolution can buy significant uplift for learning at little expense from the complexity standpoint.

Private federated learning on vertically partitioned data via entity resolution and additively homomorphic encryption

Consider two data providers, each maintaining private records of different feature sets about common entities. They aim to learn a linear model jointly in a federated setting, namely, data is local and a shared model is trained from locally computed updates. In contrast with most work on distributed learning, in this scenario (i) data is split vertically, i.e. by features, (ii) only one data provider knows the target variable and (iii) entities are not linked across the data providers. Hence, to the challenge of private learning, we add the potentially negative consequences of mistakes in entity resolution. Our contribution is twofold. First, we describe a three-party end-to-end solution in two phases ---privacy-preserving entity resolution and federated logistic regression over messages encrypted with an additively homomorphic scheme---, secure against a honest-but-curious adversary. The system allows learning without either exposing data in the clear or sharing which entities the data providers have in common. Our implementation is as accurate as a naive non-private solution that brings all data in one place, and scales to problems with millions of entities with hundreds of features. Second, we provide what is to our knowledge the first formal analysis of the impact of entity resolution's mistakes on learning, with results on how optimal classifiers, empirical losses, margins and generalisation abilities are affected. Our results bring a clear and strong support for federated learning: under reasonable assumptions on the number and magnitude of entity resolution's mistakes, it can be extremely beneficial to carry out federated learning in the setting where each peer's data provides a significant uplift to the other.

Fast Learning from Distributed Datasets without Entity Matching

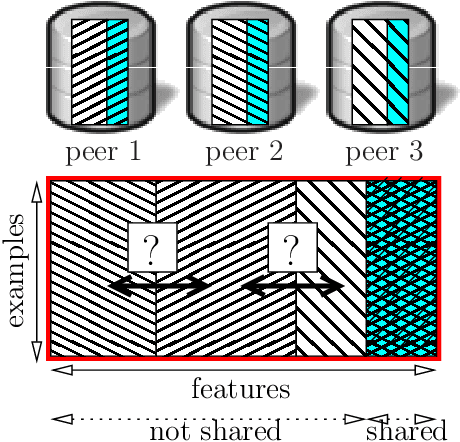
Consider the following data fusion scenario: two datasets/peers contain the same real-world entities described using partially shared features, e.g. banking and insurance company records of the same customer base. Our goal is to learn a classifier in the cross product space of the two domains, in the hard case in which no shared ID is available -- e.g. due to anonymization. Traditionally, the problem is approached by first addressing entity matching and subsequently learning the classifier in a standard manner. We present an end-to-end solution which bypasses matching entities, based on the recently introduced concept of Rademacher observations (rados). Informally, we replace the minimisation of a loss over examples, which requires to solve entity resolution, by the equivalent minimisation of a (different) loss over rados. Among others, key properties we show are (i) a potentially huge subset of these rados does not require to perform entity matching, and (ii) the algorithm that provably minimizes the rado loss over these rados has time and space complexities smaller than the algorithm minimizing the equivalent example loss. Last, we relax a key assumption of the model, that the data is vertically partitioned among peers --- in this case, we would not even know the existence of a solution to entity resolution. In this more general setting, experiments validate the possibility of significantly beating even the optimal peer in hindsight.