Tiberio Caetano
NICTA and Australian National University
Fast Fair Regression via Efficient Approximations of Mutual Information
Feb 14, 2020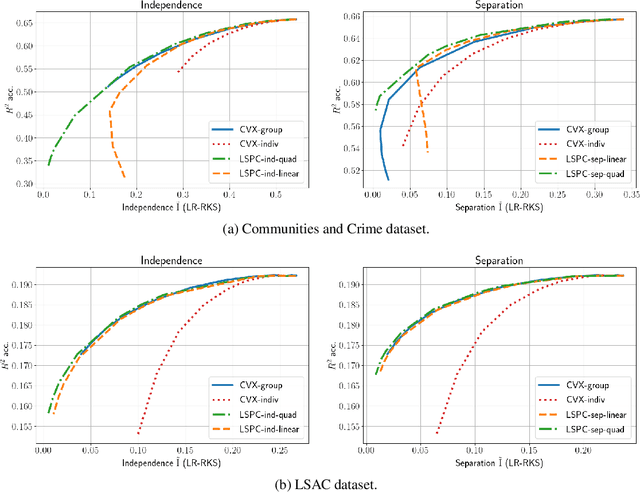
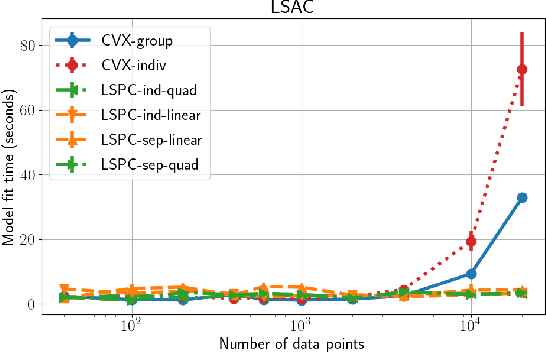
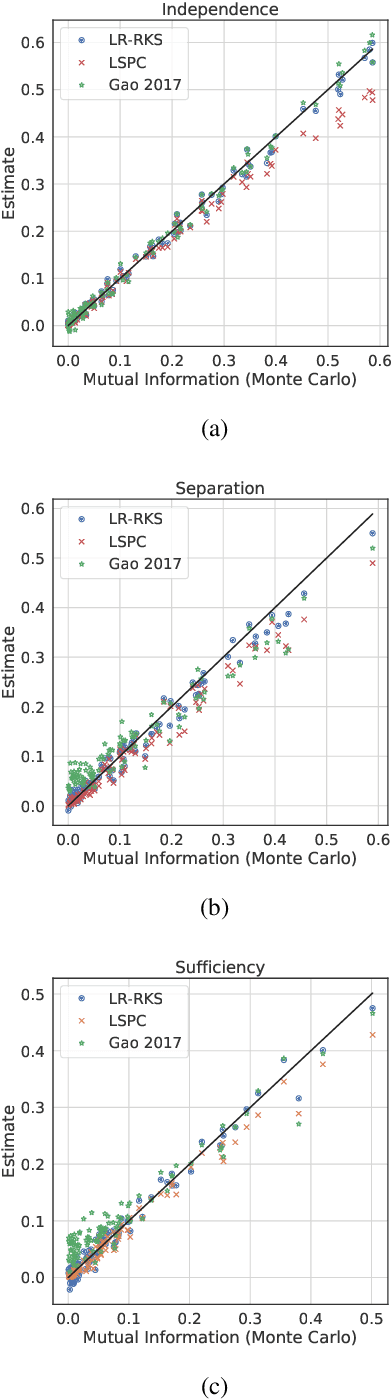
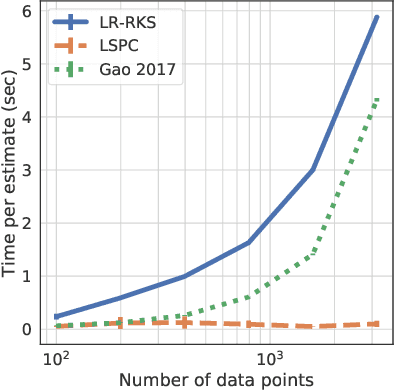
Abstract:Most work in algorithmic fairness to date has focused on discrete outcomes, such as deciding whether to grant someone a loan or not. In these classification settings, group fairness criteria such as independence, separation and sufficiency can be measured directly by comparing rates of outcomes between subpopulations. Many important problems however require the prediction of a real-valued outcome, such as a risk score or insurance premium. In such regression settings, measuring group fairness criteria is computationally challenging, as it requires estimating information-theoretic divergences between conditional probability density functions. This paper introduces fast approximations of the independence, separation and sufficiency group fairness criteria for regression models from their (conditional) mutual information definitions, and uses such approximations as regularisers to enforce fairness within a regularised risk minimisation framework. Experiments in real-world datasets indicate that in spite of its superior computational efficiency our algorithm still displays state-of-the-art accuracy/fairness tradeoffs.
The Crossover Process: Learnability and Data Protection from Inference Attacks
Mar 07, 2017
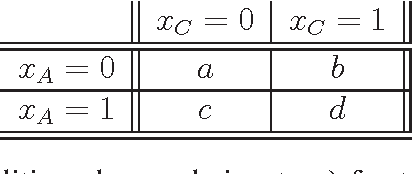
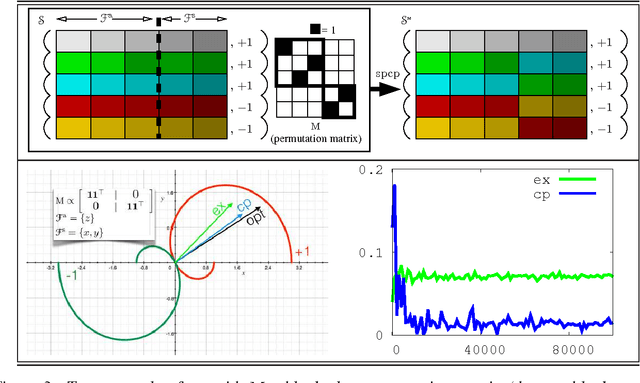

Abstract:It is usual to consider data protection and learnability as conflicting objectives. This is not always the case: we show how to jointly control inference --- seen as the attack --- and learnability by a noise-free process that mixes training examples, the Crossover Process (cp). One key point is that the cp~is typically able to alter joint distributions without touching on marginals, nor altering the sufficient statistic for the class. In other words, it saves (and sometimes improves) generalization for supervised learning, but can alter the relationship between covariates --- and therefore fool measures of nonlinear independence and causal inference into misleading ad-hoc conclusions. For example, a cp~can increase / decrease odds ratios, bring fairness or break fairness, tamper with disparate impact, strengthen, weaken or reverse causal directions, change observed statistical measures of dependence. For each of these, we quantify changes brought by a cp, as well as its statistical impact on generalization abilities via a new complexity measure that we call the Rademacher cp~complexity. Experiments on a dozen readily available domains validate the theory.
Fast Learning from Distributed Datasets without Entity Matching
Mar 13, 2016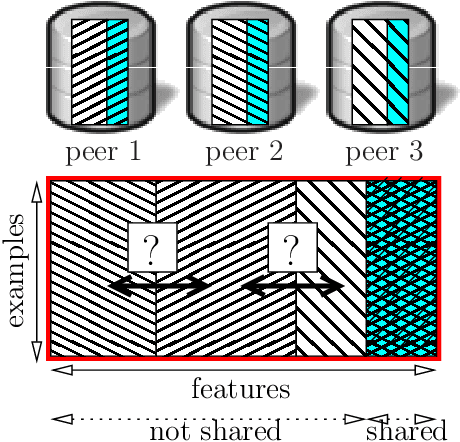



Abstract:Consider the following data fusion scenario: two datasets/peers contain the same real-world entities described using partially shared features, e.g. banking and insurance company records of the same customer base. Our goal is to learn a classifier in the cross product space of the two domains, in the hard case in which no shared ID is available -- e.g. due to anonymization. Traditionally, the problem is approached by first addressing entity matching and subsequently learning the classifier in a standard manner. We present an end-to-end solution which bypasses matching entities, based on the recently introduced concept of Rademacher observations (rados). Informally, we replace the minimisation of a loss over examples, which requires to solve entity resolution, by the equivalent minimisation of a (different) loss over rados. Among others, key properties we show are (i) a potentially huge subset of these rados does not require to perform entity matching, and (ii) the algorithm that provably minimizes the rado loss over these rados has time and space complexities smaller than the algorithm minimizing the equivalent example loss. Last, we relax a key assumption of the model, that the data is vertically partitioned among peers --- in this case, we would not even know the existence of a solution to entity resolution. In this more general setting, experiments validate the possibility of significantly beating even the optimal peer in hindsight.
A Hybrid Loss for Multiclass and Structured Prediction
Feb 09, 2014



Abstract:We propose a novel hybrid loss for multiclass and structured prediction problems that is a convex combination of a log loss for Conditional Random Fields (CRFs) and a multiclass hinge loss for Support Vector Machines (SVMs). We provide a sufficient condition for when the hybrid loss is Fisher consistent for classification. This condition depends on a measure of dominance between labels--specifically, the gap between the probabilities of the best label and the second best label. We also prove Fisher consistency is necessary for parametric consistency when learning models such as CRFs. We demonstrate empirically that the hybrid loss typically performs least as well as--and often better than--both of its constituent losses on a variety of tasks, such as human action recognition. In doing so we also provide an empirical comparison of the efficacy of probabilistic and margin based approaches to multiclass and structured prediction.
A Graphical Model Formulation of Collaborative Filtering Neighbourhood Methods with Fast Maximum Entropy Training
Jun 18, 2012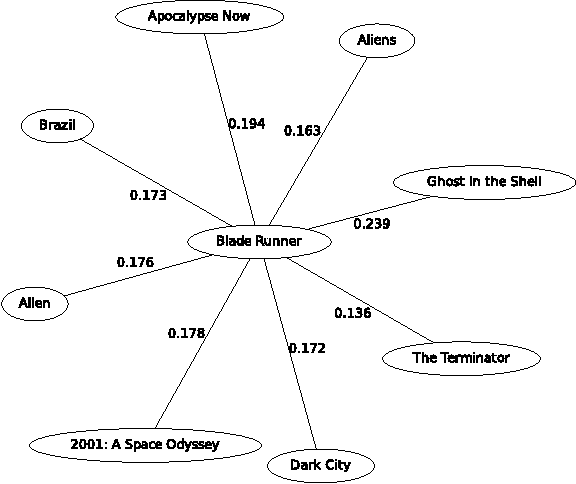

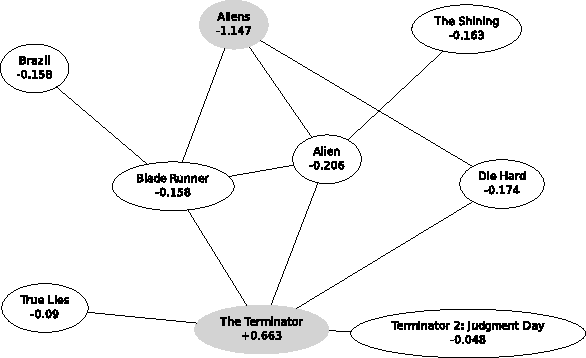
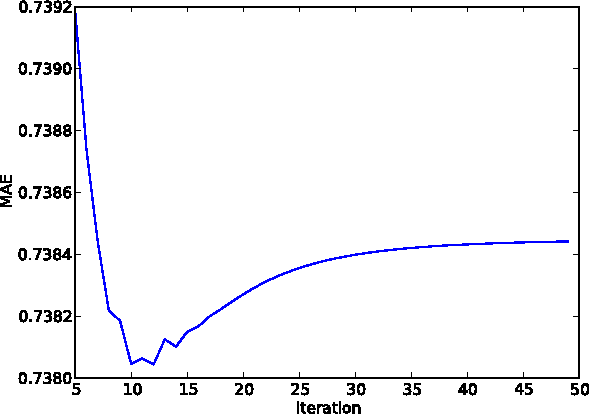
Abstract:Item neighbourhood methods for collaborative filtering learn a weighted graph over the set of items, where each item is connected to those it is most similar to. The prediction of a user's rating on an item is then given by that rating of neighbouring items, weighted by their similarity. This paper presents a new neighbourhood approach which we call item fields, whereby an undirected graphical model is formed over the item graph. The resulting prediction rule is a simple generalization of the classical approaches, which takes into account non-local information in the graph, allowing its best results to be obtained when using drastically fewer edges than other neighbourhood approaches. A fast approximate maximum entropy training method based on the Bethe approximation is presented, which uses a simple gradient ascent procedure. When using precomputed sufficient statistics on the Movielens datasets, our method is faster than maximum likelihood approaches by two orders of magnitude.
Conditional Random Fields and Support Vector Machines: A Hybrid Approach
Sep 17, 2010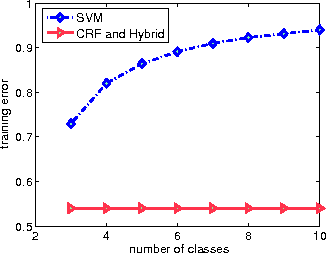

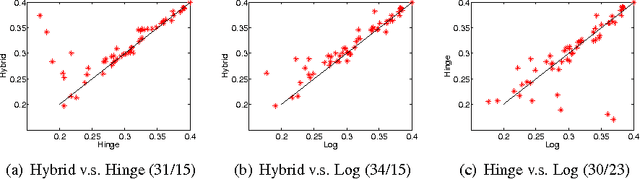
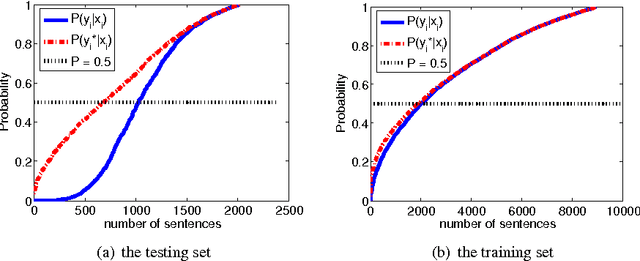
Abstract:We propose a novel hybrid loss for multiclass and structured prediction problems that is a convex combination of log loss for Conditional Random Fields (CRFs) and a multiclass hinge loss for Support Vector Machines (SVMs). We provide a sufficient condition for when the hybrid loss is Fisher consistent for classification. This condition depends on a measure of dominance between labels - specifically, the gap in per observation probabilities between the most likely labels. We also prove Fisher consistency is necessary for parametric consistency when learning models such as CRFs. We demonstrate empirically that the hybrid loss typically performs as least as well as - and often better than - both of its constituent losses on variety of tasks. In doing so we also provide an empirical comparison of the efficacy of probabilistic and margin based approaches to multiclass and structured prediction and the effects of label dominance on these results.
Scalable Inference for Latent Dirichlet Allocation
Sep 25, 2009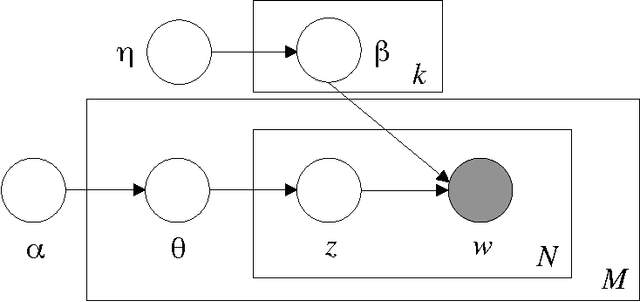


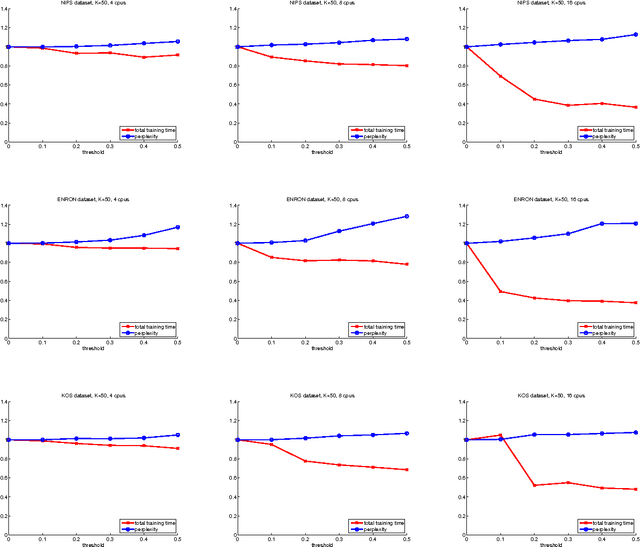
Abstract:We investigate the problem of learning a topic model - the well-known Latent Dirichlet Allocation - in a distributed manner, using a cluster of C processors and dividing the corpus to be learned equally among them. We propose a simple approximated method that can be tuned, trading speed for accuracy according to the task at hand. Our approach is asynchronous, and therefore suitable for clusters of heterogenous machines.
Exponential Family Graph Matching and Ranking
Jun 05, 2009


Abstract:We present a method for learning max-weight matching predictors in bipartite graphs. The method consists of performing maximum a posteriori estimation in exponential families with sufficient statistics that encode permutations and data features. Although inference is in general hard, we show that for one very relevant application - web page ranking - exact inference is efficient. For general model instances, an appropriate sampler is readily available. Contrary to existing max-margin matching models, our approach is statistically consistent and, in addition, experiments with increasing sample sizes indicate superior improvement over such models. We apply the method to graph matching in computer vision as well as to a standard benchmark dataset for learning web page ranking, in which we obtain state-of-the-art results, in particular improving on max-margin variants. The drawback of this method with respect to max-margin alternatives is its runtime for large graphs, which is comparatively high.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge