Fast Learning from Distributed Datasets without Entity Matching
Paper and Code
Mar 13, 2016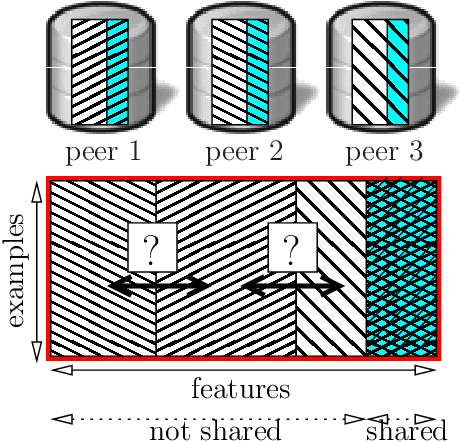



Consider the following data fusion scenario: two datasets/peers contain the same real-world entities described using partially shared features, e.g. banking and insurance company records of the same customer base. Our goal is to learn a classifier in the cross product space of the two domains, in the hard case in which no shared ID is available -- e.g. due to anonymization. Traditionally, the problem is approached by first addressing entity matching and subsequently learning the classifier in a standard manner. We present an end-to-end solution which bypasses matching entities, based on the recently introduced concept of Rademacher observations (rados). Informally, we replace the minimisation of a loss over examples, which requires to solve entity resolution, by the equivalent minimisation of a (different) loss over rados. Among others, key properties we show are (i) a potentially huge subset of these rados does not require to perform entity matching, and (ii) the algorithm that provably minimizes the rado loss over these rados has time and space complexities smaller than the algorithm minimizing the equivalent example loss. Last, we relax a key assumption of the model, that the data is vertically partitioned among peers --- in this case, we would not even know the existence of a solution to entity resolution. In this more general setting, experiments validate the possibility of significantly beating even the optimal peer in hindsight.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge