Conditional Random Fields and Support Vector Machines: A Hybrid Approach
Paper and Code
Sep 17, 2010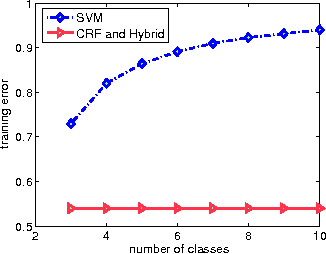

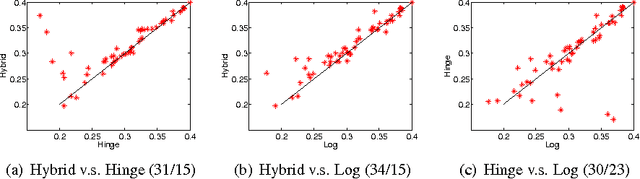
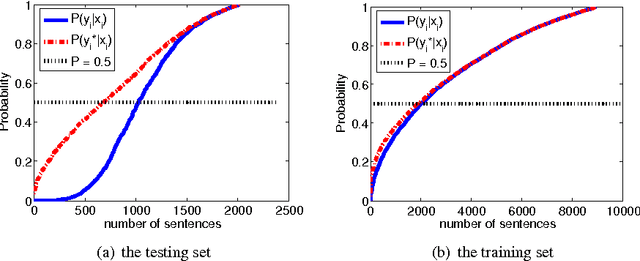
We propose a novel hybrid loss for multiclass and structured prediction problems that is a convex combination of log loss for Conditional Random Fields (CRFs) and a multiclass hinge loss for Support Vector Machines (SVMs). We provide a sufficient condition for when the hybrid loss is Fisher consistent for classification. This condition depends on a measure of dominance between labels - specifically, the gap in per observation probabilities between the most likely labels. We also prove Fisher consistency is necessary for parametric consistency when learning models such as CRFs. We demonstrate empirically that the hybrid loss typically performs as least as well as - and often better than - both of its constituent losses on variety of tasks. In doing so we also provide an empirical comparison of the efficacy of probabilistic and margin based approaches to multiclass and structured prediction and the effects of label dominance on these results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge