Causal Bandits: Learning Good Interventions via Causal Inference

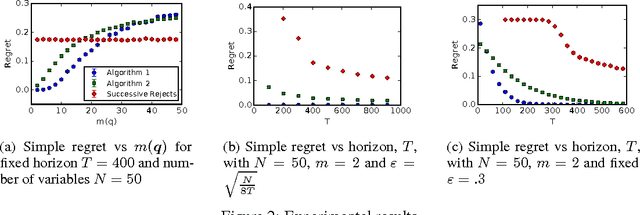
We study the problem of using causal models to improve the rate at which good interventions can be learned online in a stochastic environment. Our formalism combines multi-arm bandits and causal inference to model a novel type of bandit feedback that is not exploited by existing approaches. We propose a new algorithm that exploits the causal feedback and prove a bound on its simple regret that is strictly better (in all quantities) than algorithms that do not use the additional causal information.

Compliance-Aware Bandits

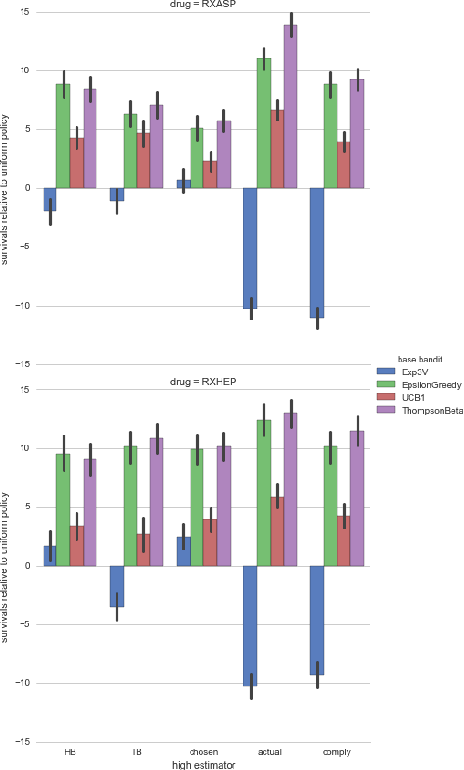
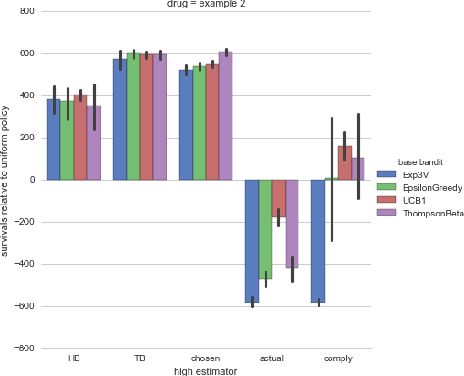
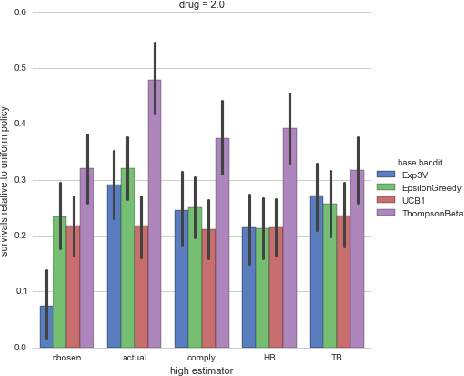
Motivated by clinical trials, we study bandits with observable non-compliance. At each step, the learner chooses an arm, after, instead of observing only the reward, it also observes the action that took place. We show that such noncompliance can be helpful or hurtful to the learner in general. Unfortunately, naively incorporating compliance information into bandit algorithms loses guarantees on sublinear regret. We present hybrid algorithms that maintain regret bounds up to a multiplicative factor and can incorporate compliance information. Simulations based on real data from the International Stoke Trial show the practical potential of these algorithms.

Fast rates in statistical and online learning

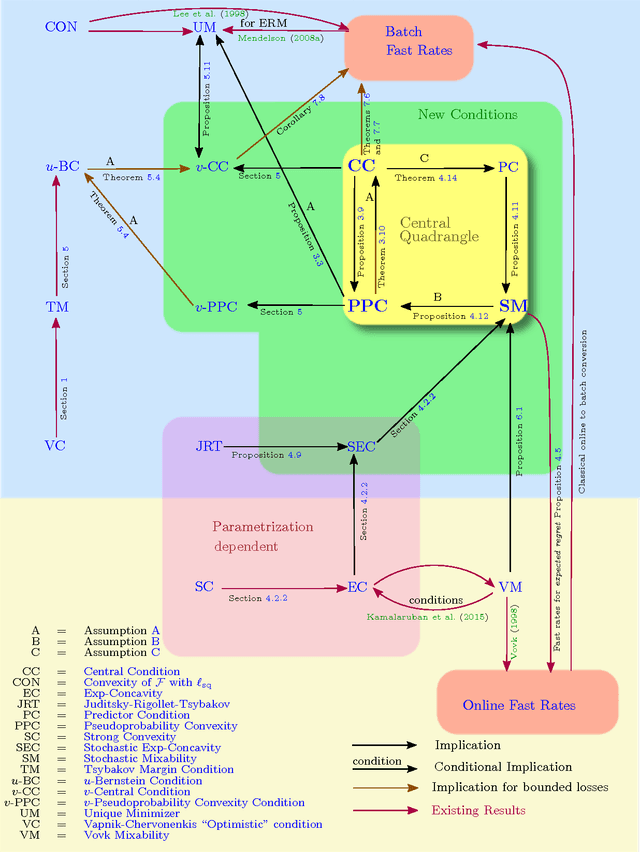
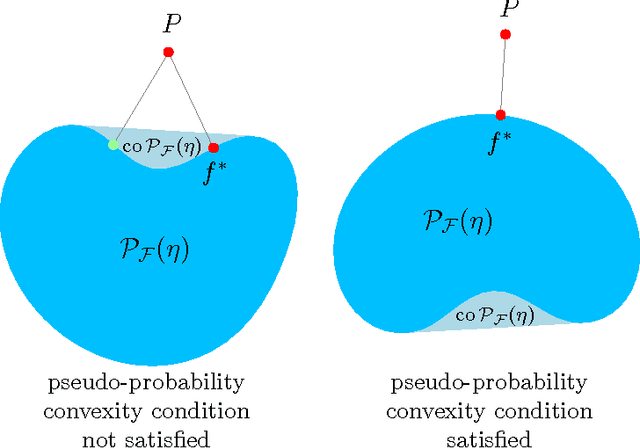
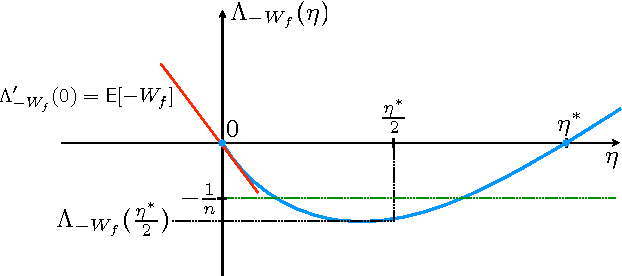
The speed with which a learning algorithm converges as it is presented with more data is a central problem in machine learning --- a fast rate of convergence means less data is needed for the same level of performance. The pursuit of fast rates in online and statistical learning has led to the discovery of many conditions in learning theory under which fast learning is possible. We show that most of these conditions are special cases of a single, unifying condition, that comes in two forms: the central condition for 'proper' learning algorithms that always output a hypothesis in the given model, and stochastic mixability for online algorithms that may make predictions outside of the model. We show that under surprisingly weak assumptions both conditions are, in a certain sense, equivalent. The central condition has a re-interpretation in terms of convexity of a set of pseudoprobabilities, linking it to density estimation under misspecification. For bounded losses, we show how the central condition enables a direct proof of fast rates and we prove its equivalence to the Bernstein condition, itself a generalization of the Tsybakov margin condition, both of which have played a central role in obtaining fast rates in statistical learning. Yet, while the Bernstein condition is two-sided, the central condition is one-sided, making it more suitable to deal with unbounded losses. In its stochastic mixability form, our condition generalizes both a stochastic exp-concavity condition identified by Juditsky, Rigollet and Tsybakov and Vovk's notion of mixability. Our unifying conditions thus provide a substantial step towards a characterization of fast rates in statistical learning, similar to how classical mixability characterizes constant regret in the sequential prediction with expert advice setting.

Risk Dynamics in Trade Networks

We introduce a new framework to model interactions among agents which seek to trade to minimize their risk with respect to some future outcome. We quantify this risk using the concept of risk measures from finance, and introduce a class of trade dynamics which allow agents to trade contracts contingent upon the future outcome. We then show that these trade dynamics exactly correspond to a variant of randomized coordinate descent. By extending the analysis of these coordinate descent methods to account for our more organic setting, we are able to show convergence rates for very general trade dynamics, showing that the market or network converges to a unique steady state. Applying these results to prediction markets, we expand on recent results by adding convergence rates and general aggregation properties. Finally, we illustrate the generality of our framework by applying it to agent interactions on a scale-free network.

Generalized Mixability via Entropic Duality

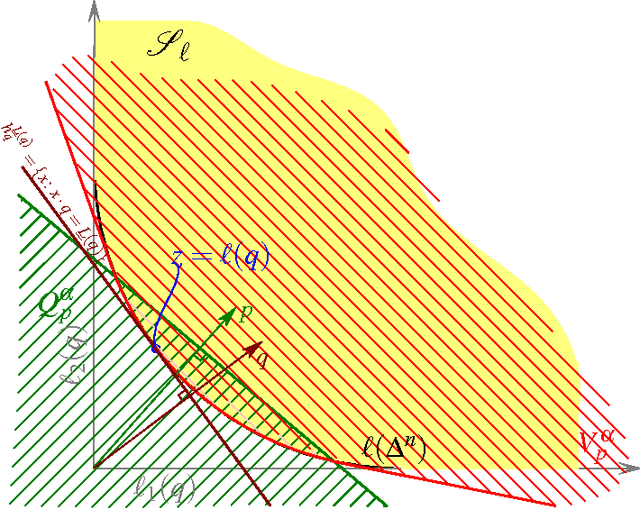
Mixability is a property of a loss which characterizes when fast convergence is possible in the game of prediction with expert advice. We show that a key property of mixability generalizes, and the exp and log operations present in the usual theory are not as special as one might have thought. In doing this we introduce a more general notion of $\Phi$-mixability where $\Phi$ is a general entropy (\ie, any convex function on probabilities). We show how a property shared by the convex dual of any such entropy yields a natural algorithm (the minimizer of a regret bound) which, analogous to the classical aggregating algorithm, is guaranteed a constant regret when used with $\Phi$-mixable losses. We characterize precisely which $\Phi$ have $\Phi$-mixable losses and put forward a number of conjectures about the optimality and relationships between different choices of entropy.

Generalised Mixability, Constant Regret, and Bayesian Updating

Mixability of a loss is known to characterise when constant regret bounds are achievable in games of prediction with expert advice through the use of Vovk's aggregating algorithm. We provide a new interpretation of mixability via convex analysis that highlights the role of the Kullback-Leibler divergence in its definition. This naturally generalises to what we call $\Phi$-mixability where the Bregman divergence $D_\Phi$ replaces the KL divergence. We prove that losses that are $\Phi$-mixable also enjoy constant regret bounds via a generalised aggregating algorithm that is similar to mirror descent.

Bandit Market Makers

We introduce a modular framework for market making. It combines cost-function based automated market makers with bandit algorithms. We obtain worst-case profits guarantee's relative to the best in hindsight within a class of natural "overround" cost functions . This combination allow us to have distribution-free guarantees on the regret of profits while preserving the bounded worst-case losses and computational tractability over combinatorial spaces of the cost function based approach. We present simulation results to better understand the practical behaviour of market makers from the framework.

AOSO-LogitBoost: Adaptive One-Vs-One LogitBoost for Multi-Class Problem

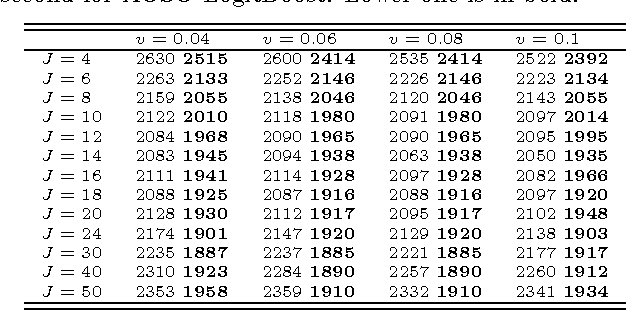
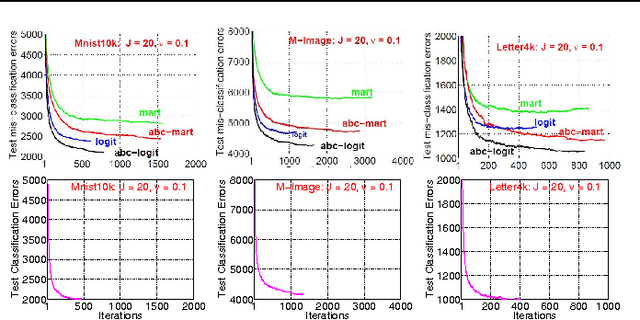
This paper presents an improvement to model learning when using multi-class LogitBoost for classification. Motivated by the statistical view, LogitBoost can be seen as additive tree regression. Two important factors in this setting are: 1) coupled classifier output due to a sum-to-zero constraint, and 2) the dense Hessian matrices that arise when computing tree node split gain and node value fittings. In general, this setting is too complicated for a tractable model learning algorithm. However, too aggressive simplification of the setting may lead to degraded performance. For example, the original LogitBoost is outperformed by ABC-LogitBoost due to the latter's more careful treatment of the above two factors. In this paper we propose techniques to address the two main difficulties of the LogitBoost setting: 1) we adopt a vector tree (i.e. each node value is vector) that enforces a sum-to-zero constraint, and 2) we use an adaptive block coordinate descent that exploits the dense Hessian when computing tree split gain and node values. Higher classification accuracy and faster convergence rates are observed for a range of public data sets when compared to both the original and the ABC-LogitBoost implementations.

Conditional Random Fields and Support Vector Machines: A Hybrid Approach

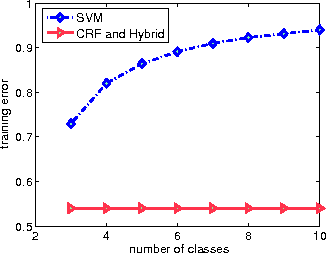
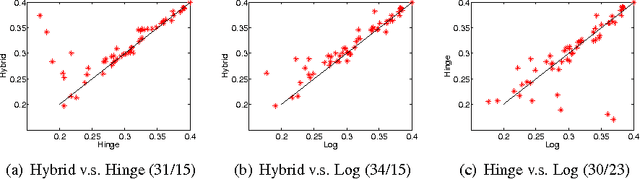
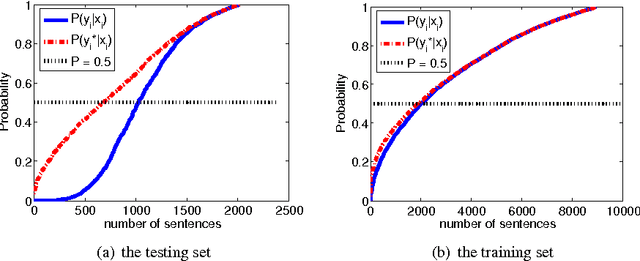
We propose a novel hybrid loss for multiclass and structured prediction problems that is a convex combination of log loss for Conditional Random Fields (CRFs) and a multiclass hinge loss for Support Vector Machines (SVMs). We provide a sufficient condition for when the hybrid loss is Fisher consistent for classification. This condition depends on a measure of dominance between labels - specifically, the gap in per observation probabilities between the most likely labels. We also prove Fisher consistency is necessary for parametric consistency when learning models such as CRFs. We demonstrate empirically that the hybrid loss typically performs as least as well as - and often better than - both of its constituent losses on variety of tasks. In doing so we also provide an empirical comparison of the efficacy of probabilistic and margin based approaches to multiclass and structured prediction and the effects of label dominance on these results.

Composite Binary Losses

We study losses for binary classification and class probability estimation and extend the understanding of them from margin losses to general composite losses which are the composition of a proper loss with a link function. We characterise when margin losses can be proper composite losses, explicitly show how to determine a symmetric loss in full from half of one of its partial losses, introduce an intrinsic parametrisation of composite binary losses and give a complete characterisation of the relationship between proper losses and ``classification calibrated'' losses. We also consider the question of the ``best'' surrogate binary loss. We introduce a precise notion of ``best'' and show there exist situations where two convex surrogate losses are incommensurable. We provide a complete explicit characterisation of the convexity of composite binary losses in terms of the link function and the weight function associated with the proper loss which make up the composite loss. This characterisation suggests new ways of ``surrogate tuning''. Finally, in an appendix we present some new algorithm-independent results on the relationship between properness, convexity and robustness to misclassification noise for binary losses and show that all convex proper losses are non-robust to misclassification noise.