Nishant Mehta
Safe-Bayesian Generalized Linear Regression
Oct 21, 2019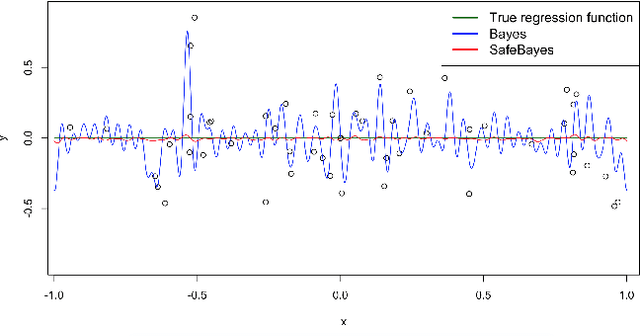
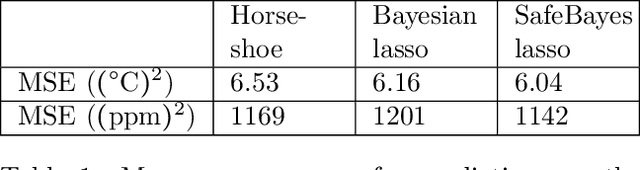
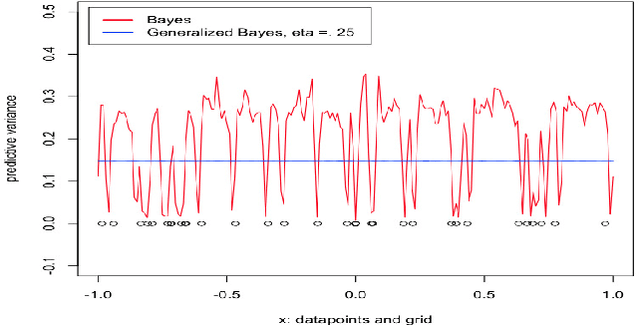

Abstract:We study generalized Bayesian inference under misspecification, i.e. when the model is `wrong but useful'. Generalized Bayes equips the likelihood with a learning rate $\eta$. We show that for generalized linear models (GLMs), $\eta$-generalized Bayes concentrates around the best approximation of the truth within the model for specific $\eta \neq 1$, even under severely misspecified noise, as long as the tails of the true distribution are exponential. We then derive MCMC samplers for generalized Bayesian lasso and logistic regression, and give examples of both simulated and real-world data in which generalized Bayes outperforms standard Bayes by a vast margin.
Generalized Mixability via Entropic Duality
Jun 24, 2014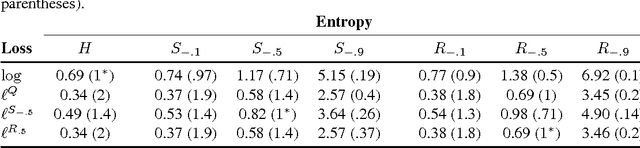
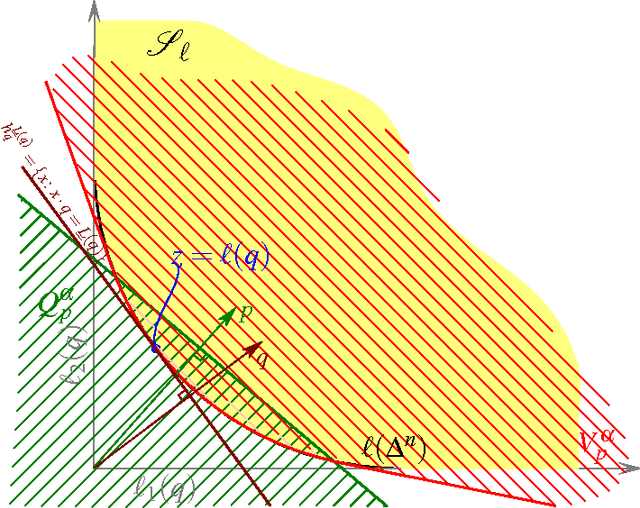
Abstract:Mixability is a property of a loss which characterizes when fast convergence is possible in the game of prediction with expert advice. We show that a key property of mixability generalizes, and the exp and log operations present in the usual theory are not as special as one might have thought. In doing this we introduce a more general notion of $\Phi$-mixability where $\Phi$ is a general entropy (\ie, any convex function on probabilities). We show how a property shared by the convex dual of any such entropy yields a natural algorithm (the minimizer of a regret bound) which, analogous to the classical aggregating algorithm, is guaranteed a constant regret when used with $\Phi$-mixable losses. We characterize precisely which $\Phi$ have $\Phi$-mixable losses and put forward a number of conjectures about the optimality and relationships between different choices of entropy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge