Minimax risk classifiers with 0-1 loss

Supervised classification techniques use training samples to learn a classification rule with small expected 0-1-loss (error probability). Conventional methods enable tractable learning and provide out-of-sample generalization by using surrogate losses instead of the 0-1-loss and considering specific families of rules (hypothesis classes). This paper presents minimax risk classifiers (MRCs) that minimize the worst-case 0-1-loss over general classification rules and provide tight performance guarantees at learning. We show that MRCs are strongly universally consistent using feature mappings given by characteristic kernels. The paper also proposes efficient optimization techniques for MRC learning and shows that the methods presented can provide accurate classification together with tight performance guarantees

PAC-Bayes, MAC-Bayes and Conditional Mutual Information: Fast rate bounds that handle general VC classes

We give a novel, unified derivation of conditional PAC-Bayesian and mutual information (MI) generalization bounds. We derive conditional MI bounds as an instance, with special choice of prior, of conditional MAC-Bayesian (Mean Approximately Correct) bounds, itself derived from conditional PAC-Bayesian bounds, where `conditional' means that one can use priors conditioned on a joint training and ghost sample. This allows us to get nontrivial PAC-Bayes and MI-style bounds for general VC classes, something recently shown to be impossible with standard PAC-Bayesian/MI bounds. Second, it allows us to get faster rates of order $O \left(({\text{KL}}/n)^{\gamma}\right)$ for $\gamma > 1/2$ if a Bernstein condition holds and for exp-concave losses (with $\gamma=1$), which is impossible with both standard PAC-Bayes generalization and MI bounds. Our work extends the recent work by Steinke and Zakynthinou [2020] who handle MI with VC but neither PAC-Bayes nor fast rates, the recent work of Hellstr\"om and Durisi [2020] who extend the latter to the PAC-Bayes setting via a unifying exponential inequality, and Mhammedi et al. [2019] who initiated fast rate PAC-Bayes generalization error bounds but handle neither MI nor general VC classes.

Safe Tests and Always-Valid Confidence Intervals for contingency tables and beyond

We develop E variables for testing whether two data streams come from the same source or not, and more generally, whether the difference between the sources is larger than some minimal effect size. These E variables lead to tests that remain safe, i.e. keep their Type-I error guarantees, under flexible sampling scenarios such as optional stopping and continuation. We also develop the corresponding always-valid confidence intervals. In special cases our E variables also have an optimal `growth' property under the alternative. We illustrate the generic construction through the special case of 2x2 contingency tables, where we also allow for the incorporation of different restrictions on a composite alternative. Comparison to p-value analysis in simulations and a real-world example show that E variables, through their flexibility, often allow for early stopping of data collection, thereby retaining similar power as classical methods.

Discovering outstanding subgroup lists for numeric targets using MDL

The task of subgroup discovery (SD) is to find interpretable descriptions of subsets of a dataset that stand out with respect to a target attribute. To address the problem of mining large numbers of redundant subgroups, subgroup set discovery (SSD) has been proposed. State-of-the-art SSD methods have their limitations though, as they typically heavily rely on heuristics and/or user-chosen hyperparameters. We propose a dispersion-aware problem formulation for subgroup set discovery that is based on the minimum description length (MDL) principle and subgroup lists. We argue that the best subgroup list is the one that best summarizes the data given the overall distribution of the target. We restrict our focus to a single numeric target variable and show that our formalization coincides with an existing quality measure when finding a single subgroup, but that-in addition-it allows to trade off subgroup quality with the complexity of the subgroup. We next propose SSD++, a heuristic algorithm for which we empirically demonstrate that it returns outstanding subgroup lists: non-redundant sets of compact subgroups that stand out by having strongly deviating means and small spread.

Safe-Bayesian Generalized Linear Regression

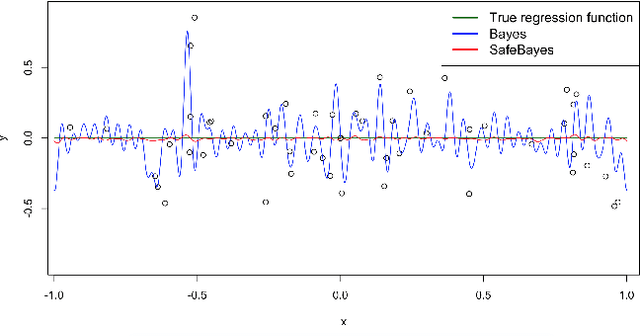
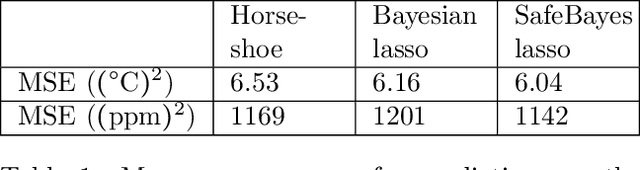
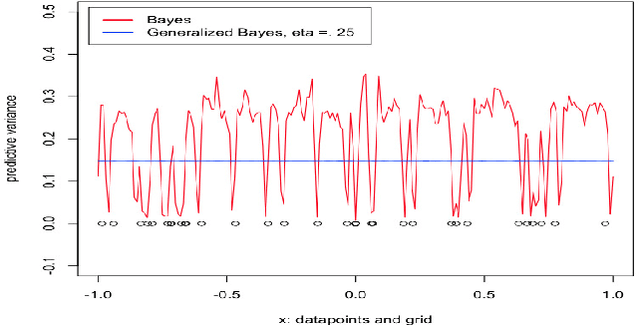
We study generalized Bayesian inference under misspecification, i.e. when the model is `wrong but useful'. Generalized Bayes equips the likelihood with a learning rate $\eta$. We show that for generalized linear models (GLMs), $\eta$-generalized Bayes concentrates around the best approximation of the truth within the model for specific $\eta \neq 1$, even under severely misspecified noise, as long as the tails of the true distribution are exponential. We then derive MCMC samplers for generalized Bayesian lasso and logistic regression, and give examples of both simulated and real-world data in which generalized Bayes outperforms standard Bayes by a vast margin.

Minimum Description Length Revisited

This is an up-to-date introduction to and overview of the Minimum Description Length (MDL) Principle, a theory of inductive inference that can be applied to general problems in statistics, machine learning and pattern recognition. While MDL was originally based on data compression ideas, this introduction can be read without any knowledge thereof. It takes into account all major developments since 2007, the last time an extensive overview was written. These include new methods for model selection and averaging and hypothesis testing, as well as the first completely general definition of {\em MDL estimators}. Incorporating these developments, MDL can be seen as a powerful extension of both penalized likelihood and Bayesian approaches, in which penalization functions and prior distributions are replaced by more general luckiness functions, average-case methodology is replaced by a more robust worst-case approach, and in which methods classically viewed as highly distinct, such as AIC vs BIC and cross-validation vs Bayes can, to a large extent, be viewed from a unified perspective.

Safe Testing

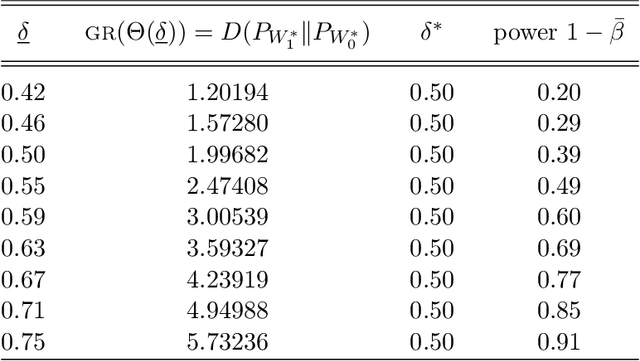
We present a new theory of hypothesis testing. The main concept is the S-value, a notion of evidence which, unlike p-values, allows for effortlessly combining evidence from several tests, even in the common scenario where the decision to perform a new test depends on the previous test outcome: safe tests based on S-values generally preserve Type-I error guarantees under such "optional continuation". S-values exist for completely general testing problems with composite null and alternatives. Their prime interpretation is in terms of gambling or investing, each S-value corresponding to a particular investment. Surprisingly, optimal "GROW" S-values, which lead to fastest capital growth, are fully characterized by the joint information projection (JIPr) between the set of all Bayes marginal distributions on H0 and H1. Thus, optimal S-values also have an interpretation as Bayes factors, with priors given by the JIPr. We illustrate the theory using two classical testing scenarios: the one-sample t-test and the 2x2 contingency table. In the t-test setting, GROW s-values correspond to adopting the right Haar prior on the variance, like in Jeffreys' Bayesian t-test. However, unlike Jeffreys', the "default" safe t-test puts a discrete 2-point prior on the effect size, leading to better behavior in terms of statistical power. Sharing Fisherian, Neymanian and Jeffreys-Bayesian interpretations, S-values and safe tests may provide a methodology acceptable to adherents of all three schools.

Optional Stopping with Bayes Factors: a categorization and extension of folklore results, with an application to invariant situations

It is often claimed that Bayesian methods, in particular Bayes factor methods for hypothesis testing, can deal with optional stopping. We first give an overview, using only most elementary probability theory, of three different mathematical meanings that various authors give to this claim: stopping rule independence, posterior calibration and (semi-) frequentist robustness to optional stopping. We then prove theorems to the effect that - while their practical implications are sometimes debatable - these claims do indeed hold in a general measure-theoretic setting. The novelty here is that we allow for nonintegrable measures based on improper priors, which leads to particularly strong results for the practically important case of models satisfying a group invariance (such as location or scale). When equipped with the right Haar prior, calibration and semi-frequentist robustness to optional stopping hold uniformly irrespective of the value of the underlying nuisance parameter, as long as the stopping rule satisfies a certain intuitive property.

Combining Adversarial Guarantees and Stochastic Fast Rates in Online Learning

We consider online learning algorithms that guarantee worst-case regret rates in adversarial environments (so they can be deployed safely and will perform robustly), yet adapt optimally to favorable stochastic environments (so they will perform well in a variety of settings of practical importance). We quantify the friendliness of stochastic environments by means of the well-known Bernstein (a.k.a. generalized Tsybakov margin) condition. For two recent algorithms (Squint for the Hedge setting and MetaGrad for online convex optimization) we show that the particular form of their data-dependent individual-sequence regret guarantees implies that they adapt automatically to the Bernstein parameters of the stochastic environment. We prove that these algorithms attain fast rates in their respective settings both in expectation and with high probability.

Safe Probability

We formalize the idea of probability distributions that lead to reliable predictions about some, but not all aspects of a domain. The resulting notion of `safety' provides a fresh perspective on foundational issues in statistics, providing a middle ground between imprecise probability and multiple-prior models on the one hand and strictly Bayesian approaches on the other. It also allows us to formalize fiducial distributions in terms of the set of random variables that they can safely predict, thus taking some of the sting out of the fiducial idea. By restricting probabilistic inference to safe uses, one also automatically avoids paradoxes such as the Monty Hall problem. Safety comes in a variety of degrees, such as "validity" (the strongest notion), "calibration", "confidence safety" and "unbiasedness" (almost the weakest notion).