Safe-Bayesian Generalized Linear Regression

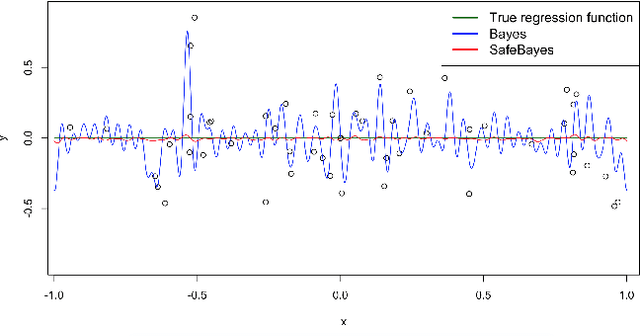
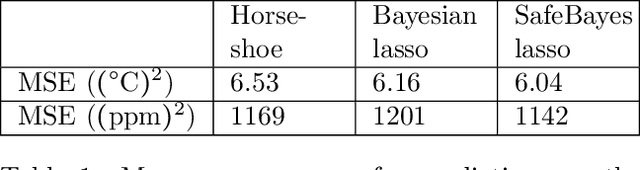
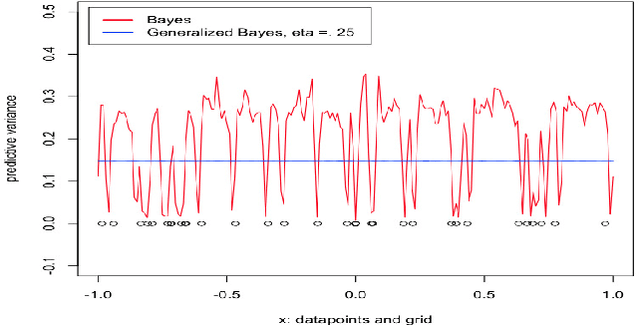
We study generalized Bayesian inference under misspecification, i.e. when the model is `wrong but useful'. Generalized Bayes equips the likelihood with a learning rate $\eta$. We show that for generalized linear models (GLMs), $\eta$-generalized Bayes concentrates around the best approximation of the truth within the model for specific $\eta \neq 1$, even under severely misspecified noise, as long as the tails of the true distribution are exponential. We then derive MCMC samplers for generalized Bayesian lasso and logistic regression, and give examples of both simulated and real-world data in which generalized Bayes outperforms standard Bayes by a vast margin.

Optimality of Poisson processes intensity learning with Gaussian processes

In this paper we provide theoretical support for the so-called "Sigmoidal Gaussian Cox Process" approach to learning the intensity of an inhomogeneous Poisson process on a $d$-dimensional domain. This method was proposed by Adams, Murray and MacKay (ICML, 2009), who developed a tractable computational approach and showed in simulation and real data experiments that it can work quite satisfactorily. The results presented in the present paper provide theoretical underpinning of the method. In particular, we show how to tune the priors on the hyper parameters of the model in order for the procedure to automatically adapt to the degree of smoothness of the unknown intensity and to achieve optimal convergence rates.