Scoring Rules and Calibration for Imprecise Probabilities

What does it mean to say that, for example, the probability for rain tomorrow is between 20% and 30%? The theory for the evaluation of precise probabilistic forecasts is well-developed and is grounded in the key concepts of proper scoring rules and calibration. For the case of imprecise probabilistic forecasts (sets of probabilities), such theory is still lacking. In this work, we therefore generalize proper scoring rules and calibration to the imprecise case. We develop these concepts as relative to data models and decision problems. As a consequence, the imprecision is embedded in a clear context. We establish a close link to the paradigm of (group) distributional robustness and in doing so provide new insights for it. We argue that proper scoring rules and calibration serve two distinct goals, which are aligned in the precise case, but intriguingly are not necessarily aligned in the imprecise case. The concept of decision-theoretic entropy plays a key role for both goals. Finally, we demonstrate the theoretical insights in machine learning practice, in particular we illustrate subtle pitfalls relating to the choice of loss function in distributional robustness.

Causal modelling without counterfactuals and individualised effects

The most common approach to causal modelling is the potential outcomes framework due to Neyman and Rubin. In this framework, outcomes of counterfactual treatments are assumed to be well-defined. This metaphysical assumption is often thought to be problematic yet indispensable. The conventional approach relies not only on counterfactuals, but also on abstract notions of distributions and assumptions of independence that are not directly testable. In this paper, we construe causal inference as treatment-wise predictions for finite populations where all assumptions are testable; this means that one can not only test predictions themselves (without any fundamental problem), but also investigate sources of error when they fail. The new framework highlights the model-dependence of causal claims as well as the difference between statistical and scientific inference.

Five reasons against assuming a data-generating distribution in Machine Learning

Machine Learning research, as most of Statistics, heavily relies on the concept of a data-generating probability distribution. As data points are thought to be sampled from such a distribution, we can learn from observed data about this distribution and, thus, predict future data points drawn from it (with some probability of success). Drawing on scholarship across disciplines, we here argue that this framework is not always a good model. Not only do such true probability distributions not exist; the framework can also be misleading and obscure both the choices made and the goals pursued in machine learning practice. We suggest an alternative framework that focuses on finite populations rather than abstract distributions; while classical learning theory can be left almost unchanged, it opens new opportunities, especially to model sampling. We compile these considerations into five reasons for modelling machine learning -- in some settings -- with finite distributions rather than generative distributions, both to be more faithful to practice and to provide novel theoretical insights.

An Axiomatic Approach to Loss Aggregation and an Adapted Aggregating Algorithm

Supervised learning has gone beyond the expected risk minimization framework. Central to most of these developments is the introduction of more general aggregation functions for losses incurred by the learner. In this paper, we turn towards online learning under expert advice. Via easily justified assumptions we characterize a set of reasonable loss aggregation functions as quasi-sums. Based upon this insight, we suggest a variant of the Aggregating Algorithm tailored to these more general aggregation functions. This variant inherits most of the nice theoretical properties of the AA, such as recovery of Bayes' updating and a time-independent bound on quasi-sum regret. Finally, we argue that generalized aggregations express the attitude of the learner towards losses.

Geometry and Stability of Supervised Learning Problems

We introduce a notion of distance between supervised learning problems, which we call the Risk distance. This optimal-transport-inspired distance facilitates stability results; one can quantify how seriously issues like sampling bias, noise, limited data, and approximations might change a given problem by bounding how much these modifications can move the problem under the Risk distance. With the distance established, we explore the geometry of the resulting space of supervised learning problems, providing explicit geodesics and proving that the set of classification problems is dense in a larger class of problems. We also provide two variants of the Risk distance: one that incorporates specified weights on a problem's predictors, and one that is more sensitive to the contours of a problem's risk landscape.

Four Facets of Forecast Felicity: Calibration, Predictiveness, Randomness and Regret

Machine learning is about forecasting. Forecasts, however, obtain their usefulness only through their evaluation. Machine learning has traditionally focused on types of losses and their corresponding regret. Currently, the machine learning community regained interest in calibration. In this work, we show the conceptual equivalence of calibration and regret in evaluating forecasts. We frame the evaluation problem as a game between a forecaster, a gambler and nature. Putting intuitive restrictions on gambler and forecaster, calibration and regret naturally fall out of the framework. In addition, this game links evaluation of forecasts to randomness of outcomes. Random outcomes with respect to forecasts are equivalent to good forecasts with respect to outcomes. We call those dual aspects, calibration and regret, predictiveness and randomness, the four facets of forecast felicity.

A General Framework for Learning under Corruption: Label Noise, Attribute Noise, and Beyond

Corruption is frequently observed in collected data and has been extensively studied in machine learning under different corruption models. Despite this, there remains a limited understanding of how these models relate such that a unified view of corruptions and their consequences on learning is still lacking. In this work, we formally analyze corruption models at the distribution level through a general, exhaustive framework based on Markov kernels. We highlight the existence of intricate joint and dependent corruptions on both labels and attributes, which are rarely touched by existing research. Further, we show how these corruptions affect standard supervised learning by analyzing the resulting changes in Bayes Risk. Our findings offer qualitative insights into the consequences of "more complex" corruptions on the learning problem, and provide a foundation for future quantitative comparisons. Applications of the framework include corruption-corrected learning, a subcase of which we study in this paper by theoretically analyzing loss correction with respect to different corruption instances.

Insights From Insurance for Fair Machine Learning: Responsibility, Performativity and Aggregates

We argue that insurance can act as an analogon for the social situatedness of machine learning systems, hence allowing machine learning scholars to take insights from the rich and interdisciplinary insurance literature. Tracing the interaction of uncertainty, fairness and responsibility in insurance provides a fresh perspective on fairness in machine learning. We link insurance fairness conceptions to their machine learning relatives, and use this bridge to problematize fairness as calibration. In this process, we bring to the forefront three themes that have been largely overlooked in the machine learning literature: responsibility, performativity and tensions between aggregate and individual.

The Geometry of Mixability

Mixable loss functions are of fundamental importance in the context of prediction with expert advice in the online setting since they characterize fast learning rates. By re-interpreting properness from the point of view of differential geometry, we provide a simple geometric characterization of mixability for the binary and multi-class cases: a proper loss function $\ell$ is $\eta$-mixable if and only if the superpredition set $\textrm{spr}(\eta \ell)$ of the scaled loss function $\eta \ell$ slides freely inside the superprediction set $\textrm{spr}(\ell_{\log})$ of the log loss $\ell_{\log}$, under fairly general assumptions on the differentiability of $\ell$. Our approach provides a way to treat some concepts concerning loss functions (like properness) in a ''coordinate-free'' manner and reconciles previous results obtained for mixable loss functions for the binary and the multi-class cases.

Tailoring to the Tails: Risk Measures for Fine-Grained Tail Sensitivity

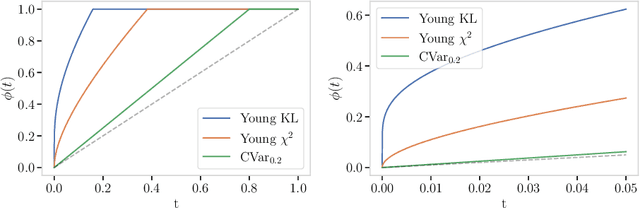
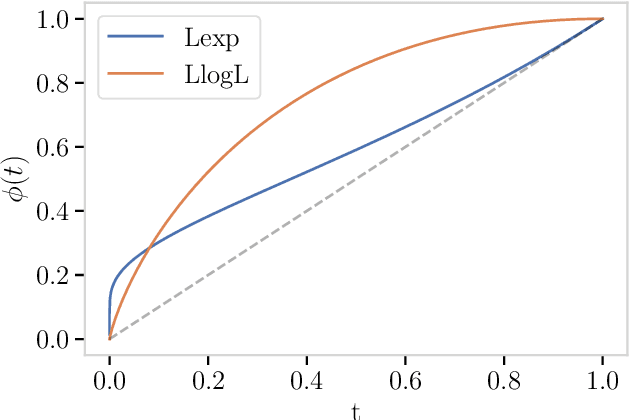
Expected risk minimization (ERM) is at the core of machine learning systems. This means that the risk inherent in a loss distribution is summarized using a single number - its average. In this paper, we propose a general approach to construct risk measures which exhibit a desired tail sensitivity and may replace the expectation operator in ERM. Our method relies on the specification of a reference distribution with a desired tail behaviour, which is in a one-to-one correspondence to a coherent upper probability. Any risk measure, which is compatible with this upper probability, displays a tail sensitivity which is finely tuned to the reference distribution. As a concrete example, we focus on divergence risk measures based on f-divergence ambiguity sets, which are a widespread tool used to foster distributional robustness of machine learning systems. For instance, we show how ambiguity sets based on the Kullback-Leibler divergence are intricately tied to the class of subexponential random variables. We elaborate the connection of divergence risk measures and rearrangement invariant Banach norms.