Scoring Rules and Calibration for Imprecise Probabilities

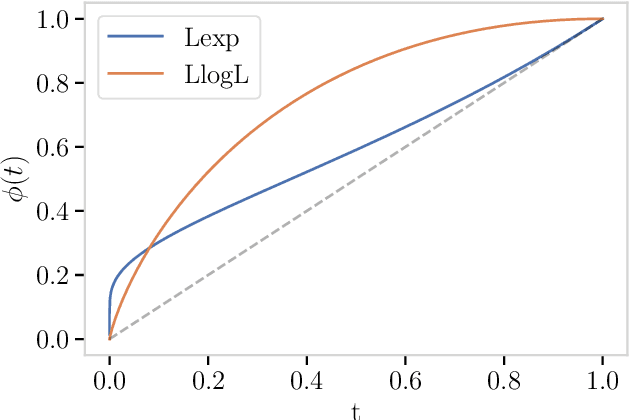
What does it mean to say that, for example, the probability for rain tomorrow is between 20% and 30%? The theory for the evaluation of precise probabilistic forecasts is well-developed and is grounded in the key concepts of proper scoring rules and calibration. For the case of imprecise probabilistic forecasts (sets of probabilities), such theory is still lacking. In this work, we therefore generalize proper scoring rules and calibration to the imprecise case. We develop these concepts as relative to data models and decision problems. As a consequence, the imprecision is embedded in a clear context. We establish a close link to the paradigm of (group) distributional robustness and in doing so provide new insights for it. We argue that proper scoring rules and calibration serve two distinct goals, which are aligned in the precise case, but intriguingly are not necessarily aligned in the imprecise case. The concept of decision-theoretic entropy plays a key role for both goals. Finally, we demonstrate the theoretical insights in machine learning practice, in particular we illustrate subtle pitfalls relating to the choice of loss function in distributional robustness.

Insights From Insurance for Fair Machine Learning: Responsibility, Performativity and Aggregates

We argue that insurance can act as an analogon for the social situatedness of machine learning systems, hence allowing machine learning scholars to take insights from the rich and interdisciplinary insurance literature. Tracing the interaction of uncertainty, fairness and responsibility in insurance provides a fresh perspective on fairness in machine learning. We link insurance fairness conceptions to their machine learning relatives, and use this bridge to problematize fairness as calibration. In this process, we bring to the forefront three themes that have been largely overlooked in the machine learning literature: responsibility, performativity and tensions between aggregate and individual.

Tailoring to the Tails: Risk Measures for Fine-Grained Tail Sensitivity

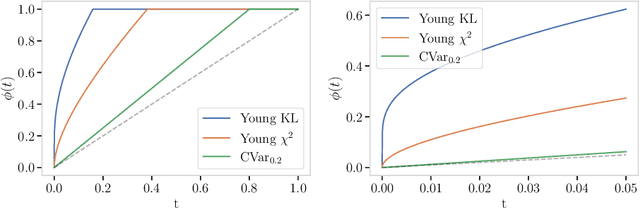
Expected risk minimization (ERM) is at the core of machine learning systems. This means that the risk inherent in a loss distribution is summarized using a single number - its average. In this paper, we propose a general approach to construct risk measures which exhibit a desired tail sensitivity and may replace the expectation operator in ERM. Our method relies on the specification of a reference distribution with a desired tail behaviour, which is in a one-to-one correspondence to a coherent upper probability. Any risk measure, which is compatible with this upper probability, displays a tail sensitivity which is finely tuned to the reference distribution. As a concrete example, we focus on divergence risk measures based on f-divergence ambiguity sets, which are a widespread tool used to foster distributional robustness of machine learning systems. For instance, we show how ambiguity sets based on the Kullback-Leibler divergence are intricately tied to the class of subexponential random variables. We elaborate the connection of divergence risk measures and rearrangement invariant Banach norms.

Risk Measures and Upper Probabilities: Coherence and Stratification

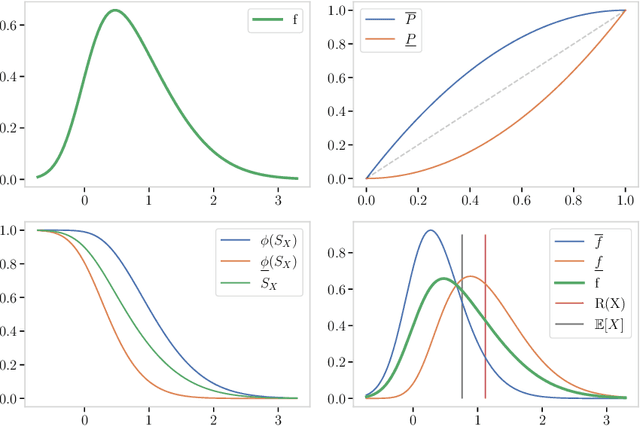
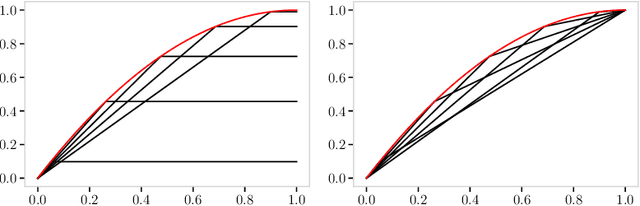
Machine learning typically presupposes classical probability theory which implies that aggregation is built upon expectation. There are now multiple reasons to motivate looking at richer alternatives to classical probability theory as a mathematical foundation for machine learning. We systematically examine a powerful and rich class of such alternatives, known variously as spectral risk measures, Choquet integrals or Lorentz norms. We present a range of characterization results, and demonstrate what makes this spectral family so special. In doing so we demonstrate a natural stratification of all coherent risk measures in terms of the upper probabilities that they induce by exploiting results from the theory of rearrangement invariant Banach spaces. We empirically demonstrate how this new approach to uncertainty helps tackling practical machine learning problems.

Teleconnection patterns of different El Niño types revealed by climate network curvature

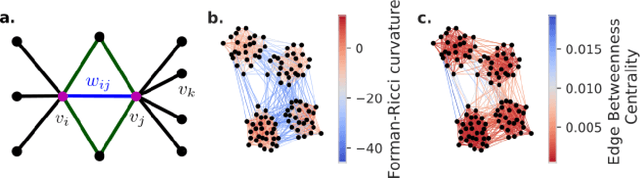
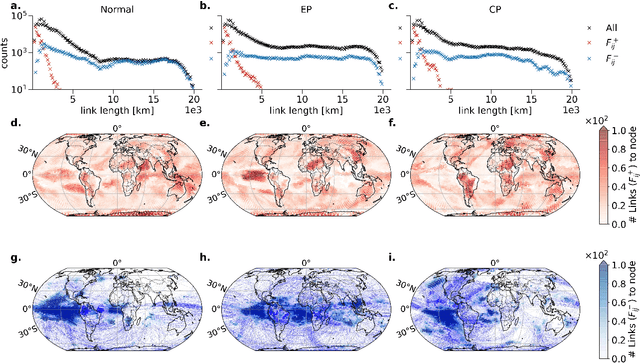
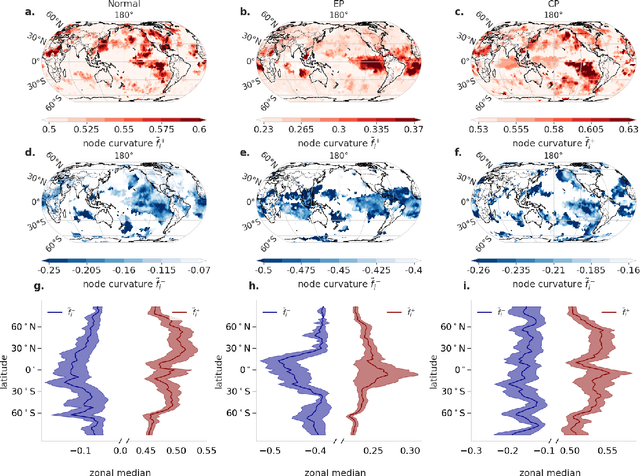
The diversity of El Ni\~no events is commonly described by two distinct flavors, the Eastern Pacific (EP) and Central Pacific (CP) types. While the remote impacts, i.e. teleconnections, of EP and CP events have been studied for different regions individually, a global picture of their teleconnection patterns is still lacking. Here, we use Forman-Ricci curvature applied on climate networks constructed from 2-meter air temperature data to distinguish regional links from teleconnections. Our results confirm that teleconnection patterns are strongly influenced by the El Ni\~no type. EP events have primarily tropical teleconnections whereas CP events involve tropical-extratropical connections, particularly in the Pacific. Moreover, the central Pacific region does not have many teleconnections, even during CP events. It is mainly the eastern Pacific that mediates the remote influences for both El Ni\~no types.

Bayesian Quadrature on Riemannian Data Manifolds

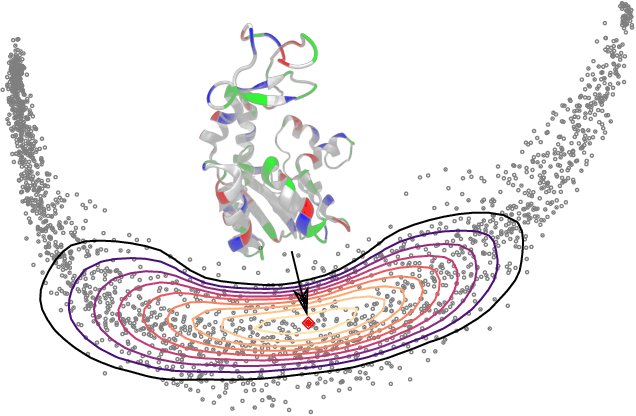
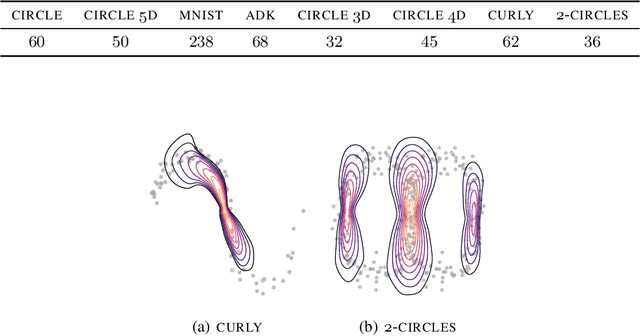
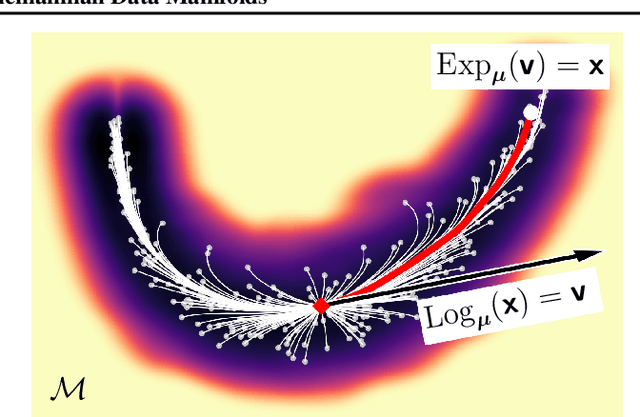
Riemannian manifolds provide a principled way to model nonlinear geometric structure inherent in data. A Riemannian metric on said manifolds determines geometry-aware shortest paths and provides the means to define statistical models accordingly. However, these operations are typically computationally demanding. To ease this computational burden, we advocate probabilistic numerical methods for Riemannian statistics. In particular, we focus on Bayesian quadrature (BQ) to numerically compute integrals over normal laws on Riemannian manifolds learned from data. In this task, each function evaluation relies on the solution of an expensive initial value problem. We show that by leveraging both prior knowledge and an active exploration scheme, BQ significantly reduces the number of required evaluations and thus outperforms Monte Carlo methods on a wide range of integration problems. As a concrete application, we highlight the merits of adopting Riemannian geometry with our proposed framework on a nonlinear dataset from molecular dynamics.