Bayesian Quadrature on Riemannian Data Manifolds
Paper and Code
Feb 12, 2021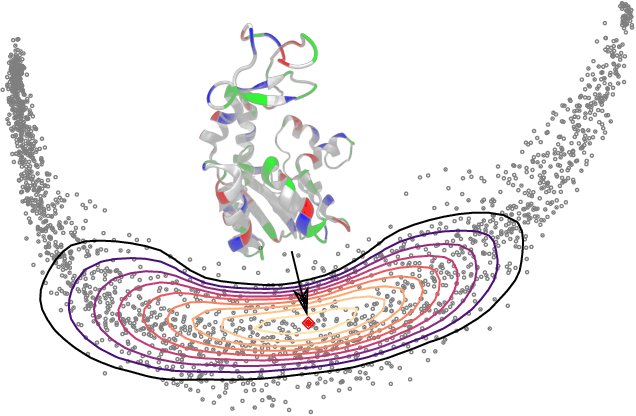
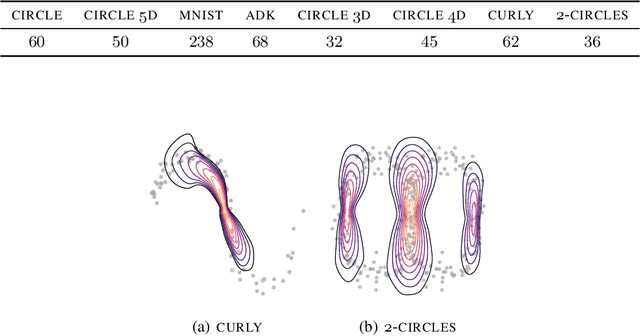
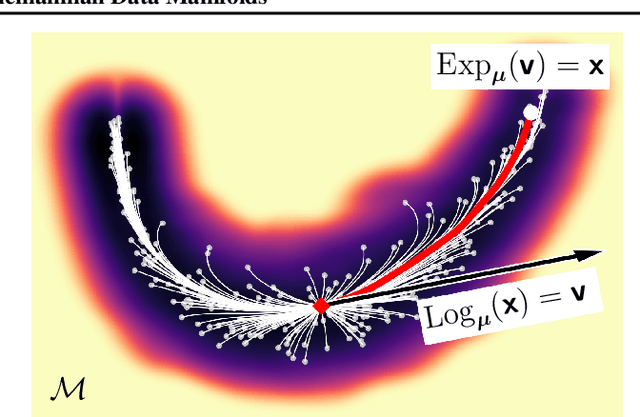

Riemannian manifolds provide a principled way to model nonlinear geometric structure inherent in data. A Riemannian metric on said manifolds determines geometry-aware shortest paths and provides the means to define statistical models accordingly. However, these operations are typically computationally demanding. To ease this computational burden, we advocate probabilistic numerical methods for Riemannian statistics. In particular, we focus on Bayesian quadrature (BQ) to numerically compute integrals over normal laws on Riemannian manifolds learned from data. In this task, each function evaluation relies on the solution of an expensive initial value problem. We show that by leveraging both prior knowledge and an active exploration scheme, BQ significantly reduces the number of required evaluations and thus outperforms Monte Carlo methods on a wide range of integration problems. As a concrete application, we highlight the merits of adopting Riemannian geometry with our proposed framework on a nonlinear dataset from molecular dynamics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge