Generalized Mixability via Entropic Duality
Paper and Code
Jun 24, 2014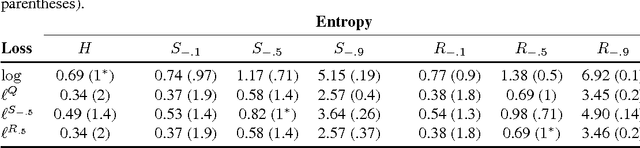
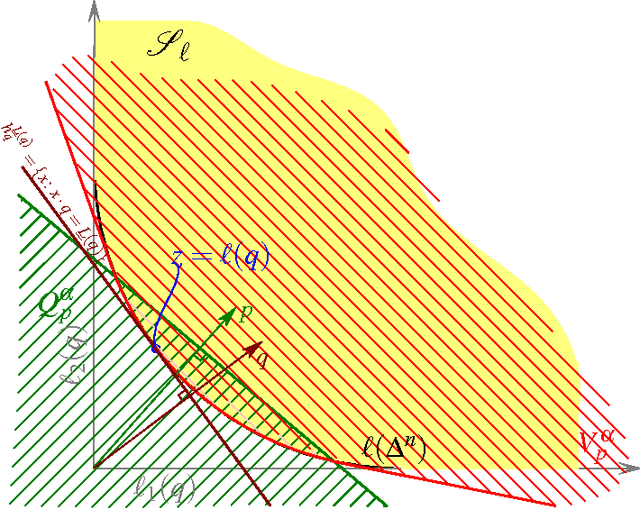
Mixability is a property of a loss which characterizes when fast convergence is possible in the game of prediction with expert advice. We show that a key property of mixability generalizes, and the exp and log operations present in the usual theory are not as special as one might have thought. In doing this we introduce a more general notion of $\Phi$-mixability where $\Phi$ is a general entropy (\ie, any convex function on probabilities). We show how a property shared by the convex dual of any such entropy yields a natural algorithm (the minimizer of a regret bound) which, analogous to the classical aggregating algorithm, is guaranteed a constant regret when used with $\Phi$-mixable losses. We characterize precisely which $\Phi$ have $\Phi$-mixable losses and put forward a number of conjectures about the optimality and relationships between different choices of entropy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge