An Embedding Framework for the Design and Analysis of Consistent Polyhedral Surrogates

We formalize and study the natural approach of designing convex surrogate loss functions via embeddings, for problems such as classification, ranking, or structured prediction. In this approach, one embeds each of the finitely many predictions (e.g. rankings) as a point in $R^d$, assigns the original loss values to these points, and "convexifies" the loss in some way to obtain a surrogate. We establish a strong connection between this approach and polyhedral (piecewise-linear convex) surrogate losses: every discrete loss is embedded by some polyhedral loss, and every polyhedral loss embeds some discrete loss. Moreover, an embedding gives rise to a consistent link function as well as linear surrogate regret bounds. Our results are constructive, as we illustrate with several examples. In particular, our framework gives succinct proofs of consistency or inconsistency for various polyhedral surrogates in the literature, and for inconsistent surrogates, it further reveals the discrete losses for which these surrogates are consistent. We go on to show additional structure of embeddings, such as the equivalence of embedding and matching Bayes risks, and the equivalence of various notions of non-redudancy. Using these results, we establish that indirect elicitation, a necessary condition for consistency, is also sufficient when working with polyhedral surrogates.

Risk Dynamics in Trade Networks

We introduce a new framework to model interactions among agents which seek to trade to minimize their risk with respect to some future outcome. We quantify this risk using the concept of risk measures from finance, and introduce a class of trade dynamics which allow agents to trade contracts contingent upon the future outcome. We then show that these trade dynamics exactly correspond to a variant of randomized coordinate descent. By extending the analysis of these coordinate descent methods to account for our more organic setting, we are able to show convergence rates for very general trade dynamics, showing that the market or network converges to a unique steady state. Applying these results to prediction markets, we expand on recent results by adding convergence rates and general aggregation properties. Finally, we illustrate the generality of our framework by applying it to agent interactions on a scale-free network.

Generalized Mixability via Entropic Duality

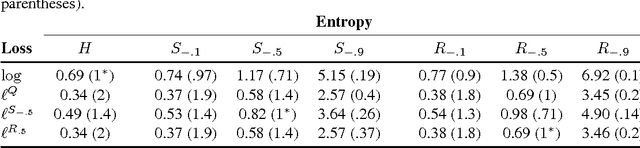
Mixability is a property of a loss which characterizes when fast convergence is possible in the game of prediction with expert advice. We show that a key property of mixability generalizes, and the exp and log operations present in the usual theory are not as special as one might have thought. In doing this we introduce a more general notion of $\Phi$-mixability where $\Phi$ is a general entropy (\ie, any convex function on probabilities). We show how a property shared by the convex dual of any such entropy yields a natural algorithm (the minimizer of a regret bound) which, analogous to the classical aggregating algorithm, is guaranteed a constant regret when used with $\Phi$-mixable losses. We characterize precisely which $\Phi$ have $\Phi$-mixable losses and put forward a number of conjectures about the optimality and relationships between different choices of entropy.

Generalised Mixability, Constant Regret, and Bayesian Updating

Mixability of a loss is known to characterise when constant regret bounds are achievable in games of prediction with expert advice through the use of Vovk's aggregating algorithm. We provide a new interpretation of mixability via convex analysis that highlights the role of the Kullback-Leibler divergence in its definition. This naturally generalises to what we call $\Phi$-mixability where the Bregman divergence $D_\Phi$ replaces the KL divergence. We prove that losses that are $\Phi$-mixable also enjoy constant regret bounds via a generalised aggregating algorithm that is similar to mirror descent.

A Collaborative Mechanism for Crowdsourcing Prediction Problems

Machine Learning competitions such as the Netflix Prize have proven reasonably successful as a method of "crowdsourcing" prediction tasks. But these competitions have a number of weaknesses, particularly in the incentive structure they create for the participants. We propose a new approach, called a Crowdsourced Learning Mechanism, in which participants collaboratively "learn" a hypothesis for a given prediction task. The approach draws heavily from the concept of a prediction market, where traders bet on the likelihood of a future event. In our framework, the mechanism continues to publish the current hypothesis, and participants can modify this hypothesis by wagering on an update. The critical incentive property is that a participant will profit an amount that scales according to how much her update improves performance on a released test set.