Trading off Consistency and Dimensionality of Convex Surrogates for the Mode

In multiclass classification over $n$ outcomes, the outcomes must be embedded into the reals with dimension at least $n-1$ in order to design a consistent surrogate loss that leads to the "correct" classification, regardless of the data distribution. For large $n$, such as in information retrieval and structured prediction tasks, optimizing a surrogate in $n-1$ dimensions is often intractable. We investigate ways to trade off surrogate loss dimension, the number of problem instances, and restricting the region of consistency in the simplex for multiclass classification. Following past work, we examine an intuitive embedding procedure that maps outcomes into the vertices of convex polytopes in a low-dimensional surrogate space. We show that full-dimensional subsets of the simplex exist around each point mass distribution for which consistency holds, but also, with less than $n-1$ dimensions, there exist distributions for which a phenomenon called hallucination occurs, which is when the optimal report under the surrogate loss is an outcome with zero probability. Looking towards application, we derive a result to check if consistency holds under a given polytope embedding and low-noise assumption, providing insight into when to use a particular embedding. We provide examples of embedding $n = 2^{d}$ outcomes into the $d$-dimensional unit cube and $n = d!$ outcomes into the $d$-dimensional permutahedron under low-noise assumptions. Finally, we demonstrate that with multiple problem instances, we can learn the mode with $\frac{n}{2}$ dimensions over the whole simplex.

Using Property Elicitation to Understand the Impacts of Fairness Constraints

Predictive algorithms are often trained by optimizing some loss function, to which regularization functions are added to impose a penalty for violating constraints. As expected, the addition of such regularization functions can change the minimizer of the objective. It is not well-understood which regularizers change the minimizer of the loss, and, when the minimizer does change, how it changes. We use property elicitation to take first steps towards understanding the joint relationship between the loss and regularization functions and the optimal decision for a given problem instance. In particular, we give a necessary and sufficient condition on loss and regularizer pairs for when a property changes with the addition of the regularizer, and examine some regularizers satisfying this condition standard in the fair machine learning literature. We empirically demonstrate how algorithmic decision-making changes as a function of both data distribution changes and hardness of the constraints.

Consistent Polyhedral Surrogates for Top-$k$ Classification and Variants

Top-$k$ classification is a generalization of multiclass classification used widely in information retrieval, image classification, and other extreme classification settings. Several hinge-like (piecewise-linear) surrogates have been proposed for the problem, yet all are either non-convex or inconsistent. For the proposed hinge-like surrogates that are convex (i.e., polyhedral), we apply the recent embedding framework of Finocchiaro et al. (2019; 2022) to determine the prediction problem for which the surrogate is consistent. These problems can all be interpreted as variants of top-$k$ classification, which may be better aligned with some applications. We leverage this analysis to derive constraints on the conditional label distributions under which these proposed surrogates become consistent for top-$k$. It has been further suggested that every convex hinge-like surrogate must be inconsistent for top-$k$. Yet, we use the same embedding framework to give the first consistent polyhedral surrogate for this problem.

An Embedding Framework for the Design and Analysis of Consistent Polyhedral Surrogates

We formalize and study the natural approach of designing convex surrogate loss functions via embeddings, for problems such as classification, ranking, or structured prediction. In this approach, one embeds each of the finitely many predictions (e.g. rankings) as a point in $R^d$, assigns the original loss values to these points, and "convexifies" the loss in some way to obtain a surrogate. We establish a strong connection between this approach and polyhedral (piecewise-linear convex) surrogate losses: every discrete loss is embedded by some polyhedral loss, and every polyhedral loss embeds some discrete loss. Moreover, an embedding gives rise to a consistent link function as well as linear surrogate regret bounds. Our results are constructive, as we illustrate with several examples. In particular, our framework gives succinct proofs of consistency or inconsistency for various polyhedral surrogates in the literature, and for inconsistent surrogates, it further reveals the discrete losses for which these surrogates are consistent. We go on to show additional structure of embeddings, such as the equivalence of embedding and matching Bayes risks, and the equivalence of various notions of non-redudancy. Using these results, we establish that indirect elicitation, a necessary condition for consistency, is also sufficient when working with polyhedral surrogates.

The Structured Abstain Problem and the Lovász Hinge

The Lov\'asz hinge is a convex surrogate recently proposed for structured binary classification, in which $k$ binary predictions are made simultaneously and the error is judged by a submodular set function. Despite its wide usage in image segmentation and related problems, its consistency has remained open. We resolve this open question, showing that the Lov\'asz hinge is inconsistent for its desired target unless the set function is modular. Leveraging a recent embedding framework, we instead derive the target loss for which the Lov\'asz hinge is consistent. This target, which we call the structured abstain problem, allows one to abstain on any subset of the $k$ predictions. We derive two link functions, each of which are consistent for all submodular set functions simultaneously.

Unifying Lower Bounds on Prediction Dimension of Consistent Convex Surrogates

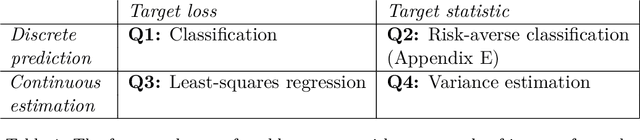
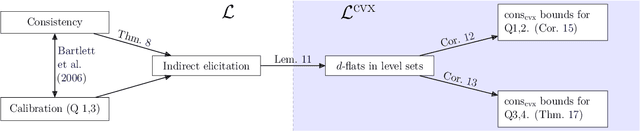
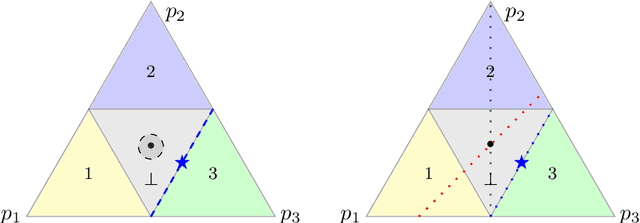
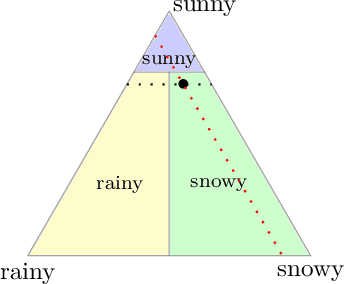
Given a prediction task, understanding when one can and cannot design a consistent convex surrogate loss, particularly a low-dimensional one, is an important and active area of machine learning research. The prediction task may be given as a target loss, as in classification and structured prediction, or simply as a (conditional) statistic of the data, as in risk measure estimation. These two scenarios typically involve different techniques for designing and analyzing surrogate losses. We unify these settings using tools from property elicitation, and give a general lower bound on prediction dimension. Our lower bound tightens existing results in the case of discrete predictions, showing that previous calibration-based bounds can largely be recovered via property elicitation. For continuous estimation, our lower bound resolves on open problem on estimating measures of risk and uncertainty.

Bridging Machine Learning and Mechanism Design towards Algorithmic Fairness

Decision-making systems increasingly orchestrate our world: how to intervene on the algorithmic components to build fair and equitable systems is therefore a question of utmost importance; one that is substantially complicated by the context-dependent nature of fairness and discrimination. Modern systems incorporate machine-learned predictions in broader decision-making pipelines, implicating concerns like constrained allocation and strategic behavior that are typically thought of as mechanism design problems. Although both machine learning and mechanism design have individually developed frameworks for addressing issues of fairness and equity, in some complex decision-making systems, neither framework is individually sufficient. In this paper, we develop the position that building fair decision-making systems requires overcoming these limitations which, we argue, are inherent to the individual frameworks of machine learning and mechanism design. Our ultimate objective is to build an encompassing framework that cohesively bridges the individual frameworks. We begin to lay the ground work towards achieving this goal by comparing the perspective each individual discipline takes on fair decision-making, teasing out the lessons each field has taught and can teach the other, and highlighting application domains that require a strong collaboration between these disciplines.

An Embedding Framework for Consistent Polyhedral Surrogates

We formalize and study the natural approach of designing convex surrogate loss functions via embeddings for problems such as classification or ranking. In this approach, one embeds each of the finitely many predictions (e.g. classes) as a point in R^d, assigns the original loss values to these points, and convexifies the loss in between to obtain a surrogate. We prove that this approach is equivalent, in a strong sense, to working with polyhedral (piecewise linear convex) losses. Moreover, given any polyhedral loss $L$, we give a construction of a link function through which $L$ is a consistent surrogate for the loss it embeds. We go on to illustrate the power of this embedding framework with succinct proofs of consistency or inconsistency of various polyhedral surrogates in the literature.