Hedging and Approximate Truthfulness in Traditional Forecasting Competitions

In forecasting competitions, the traditional mechanism scores the predictions of each contestant against the outcome of each event, and the contestant with the highest total score wins. While it is well-known that this traditional mechanism can suffer from incentive issues, it is folklore that contestants will still be roughly truthful as the number of events grows. Yet thus far the literature lacks a formal analysis of this traditional mechanism. This paper gives the first such analysis. We first demonstrate that the ''long-run truthfulness'' folklore is false: even for arbitrary numbers of events, the best forecaster can have an incentive to hedge, reporting more moderate beliefs to increase their win probability. On the positive side, however, we show that two contestants will be approximately truthful when they have sufficient uncertainty over the relative quality of their opponent and the outcomes of the events, a case which may arise in practice.

Forecasting Competitions with Correlated Events

Beginning with Witkowski et al. [2022], recent work on forecasting competitions has addressed incentive problems with the common winner-take-all mechanism. Frongillo et al. [2021] propose a competition mechanism based on follow-the-regularized-leader (FTRL), an online learning framework. They show that their mechanism selects an $\epsilon$-optimal forecaster with high probability using only $O(\log(n)/\epsilon^2)$ events. These works, together with all prior work on this problem thus far, assume that events are independent. We initiate the study of forecasting competitions for correlated events. To quantify correlation, we introduce a notion of block correlation, which allows each event to be strongly correlated with up to $b$ others. We show that under distributions with this correlation, the FTRL mechanism retains its $\epsilon$-optimal guarantee using $O(b^2 \log(n)/\epsilon^2)$ events. Our proof involves a novel concentration bound for correlated random variables which may be of broader interest.

Proper losses for discrete generative models

We initiate the study of proper losses for evaluating generative models in the discrete setting. Unlike traditional proper losses, we treat both the generative model and the target distribution as black-boxes, only assuming ability to draw i.i.d. samples. We define a loss to be black-box proper if the generative distribution that minimizes expected loss is equal to the target distribution. Using techniques from statistical estimation theory, we give a general construction and characterization of black-box proper losses: they must take a polynomial form, and the number of draws from the model and target distribution must exceed the degree of the polynomial. The characterization rules out a loss whose expectation is the cross-entropy between the target distribution and the model. By extending the construction to arbitrary sampling schemes such as Poisson sampling, however, we show that one can construct such a loss.

Consistent Polyhedral Surrogates for Top-$k$ Classification and Variants

Top-$k$ classification is a generalization of multiclass classification used widely in information retrieval, image classification, and other extreme classification settings. Several hinge-like (piecewise-linear) surrogates have been proposed for the problem, yet all are either non-convex or inconsistent. For the proposed hinge-like surrogates that are convex (i.e., polyhedral), we apply the recent embedding framework of Finocchiaro et al. (2019; 2022) to determine the prediction problem for which the surrogate is consistent. These problems can all be interpreted as variants of top-$k$ classification, which may be better aligned with some applications. We leverage this analysis to derive constraints on the conditional label distributions under which these proposed surrogates become consistent for top-$k$. It has been further suggested that every convex hinge-like surrogate must be inconsistent for top-$k$. Yet, we use the same embedding framework to give the first consistent polyhedral surrogate for this problem.

The Structured Abstain Problem and the Lovász Hinge

The Lov\'asz hinge is a convex surrogate recently proposed for structured binary classification, in which $k$ binary predictions are made simultaneously and the error is judged by a submodular set function. Despite its wide usage in image segmentation and related problems, its consistency has remained open. We resolve this open question, showing that the Lov\'asz hinge is inconsistent for its desired target unless the set function is modular. Leveraging a recent embedding framework, we instead derive the target loss for which the Lov\'asz hinge is consistent. This target, which we call the structured abstain problem, allows one to abstain on any subset of the $k$ predictions. We derive two link functions, each of which are consistent for all submodular set functions simultaneously.

No-Regret Learning in Games is Turing Complete

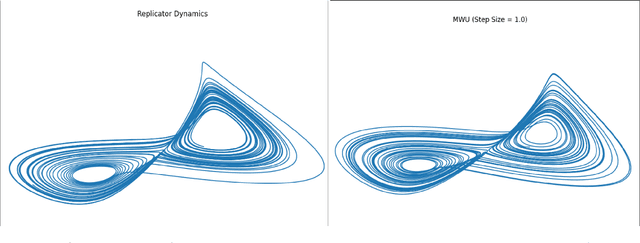
Games are natural models for multi-agent machine learning settings, such as generative adversarial networks (GANs). The desirable outcomes from algorithmic interactions in these games are encoded as game theoretic equilibrium concepts, e.g. Nash and coarse correlated equilibria. As directly computing an equilibrium is typically impractical, one often aims to design learning algorithms that iteratively converge to equilibria. A growing body of negative results casts doubt on this goal, from non-convergence to chaotic and even arbitrary behaviour. In this paper we add a strong negative result to this list: learning in games is Turing complete. Specifically, we prove Turing completeness of the replicator dynamic on matrix games, one of the simplest possible settings. Our results imply the undecicability of reachability problems for learning algorithms in games, a special case of which is determining equilibrium convergence.

Surrogate Regret Bounds for Polyhedral Losses

Surrogate risk minimization is an ubiquitous paradigm in supervised machine learning, wherein a target problem is solved by minimizing a surrogate loss on a dataset. Surrogate regret bounds, also called excess risk bounds, are a common tool to prove generalization rates for surrogate risk minimization. While surrogate regret bounds have been developed for certain classes of loss functions, such as proper losses, general results are relatively sparse. We provide two general results. The first gives a linear surrogate regret bound for any polyhedral (piecewise-linear and convex) surrogate, meaning that surrogate generalization rates translate directly to target rates. The second shows that for sufficiently non-polyhedral surrogates, the regret bound is a square root, meaning fast surrogate generalization rates translate to slow rates for the target. Together, these results suggest polyhedral surrogates are optimal in many cases.

Learning in Matrix Games can be Arbitrarily Complex

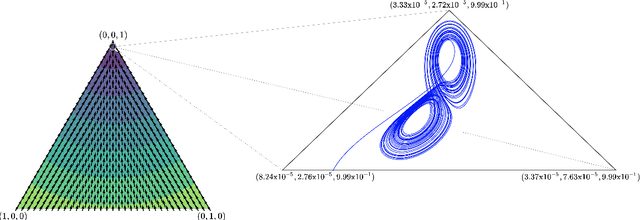
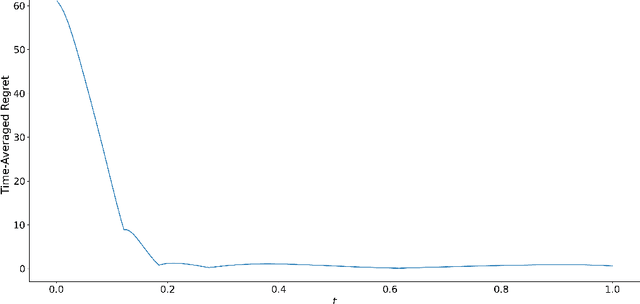
A growing number of machine learning architectures, such as Generative Adversarial Networks, rely on the design of games which implement a desired functionality via a Nash equilibrium. In practice these games have an implicit complexity (e.g. from underlying datasets and the deep networks used) that makes directly computing a Nash equilibrium impractical or impossible. For this reason, numerous learning algorithms have been developed with the goal of iteratively converging to a Nash equilibrium. Unfortunately, the dynamics generated by the learning process can be very intricate and instances of training failure hard to interpret. In this paper we show that, in a strong sense, this dynamic complexity is inherent to games. Specifically, we prove that replicator dynamics, the continuous-time analogue of Multiplicative Weights Update, even when applied in a very restricted class of games -- known as finite matrix games -- is rich enough to be able to approximate arbitrary dynamical systems. Our results are positive in the sense that they show the nearly boundless dynamic modelling capabilities of current machine learning practices, but also negative in implying that these capabilities may come at the cost of interpretability. As a concrete example, we show how replicator dynamics can effectively reproduce the well-known strange attractor of Lonrenz dynamics (the "butterfly effect") while achieving no regret.

Efficient Competitions and Online Learning with Strategic Forecasters

Winner-take-all competitions in forecasting and machine-learning suffer from distorted incentives. Witkowskiet al. identified this problem and proposed ELF, a truthful mechanism to select a winner. We show that, from a pool of $n$ forecasters, ELF requires $\Theta(n\log n)$ events or test data points to select a near-optimal forecaster with high probability. We then show that standard online learning algorithms select an $\epsilon$-optimal forecaster using only $O(\log(n) / \epsilon^2)$ events, by way of a strong approximate-truthfulness guarantee. This bound matches the best possible even in the nonstrategic setting. We then apply these mechanisms to obtain the first no-regret guarantee for non-myopic strategic experts.

Unifying Lower Bounds on Prediction Dimension of Consistent Convex Surrogates

Given a prediction task, understanding when one can and cannot design a consistent convex surrogate loss, particularly a low-dimensional one, is an important and active area of machine learning research. The prediction task may be given as a target loss, as in classification and structured prediction, or simply as a (conditional) statistic of the data, as in risk measure estimation. These two scenarios typically involve different techniques for designing and analyzing surrogate losses. We unify these settings using tools from property elicitation, and give a general lower bound on prediction dimension. Our lower bound tightens existing results in the case of discrete predictions, showing that previous calibration-based bounds can largely be recovered via property elicitation. For continuous estimation, our lower bound resolves on open problem on estimating measures of risk and uncertainty.