No-Regret Learning in Games is Turing Complete
Paper and Code
Feb 24, 2022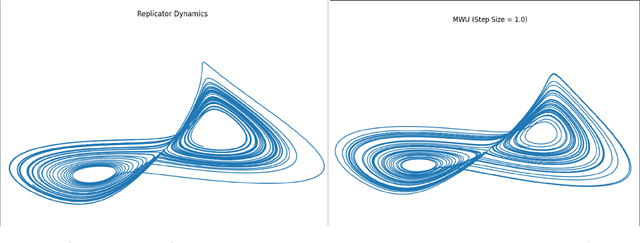
Games are natural models for multi-agent machine learning settings, such as generative adversarial networks (GANs). The desirable outcomes from algorithmic interactions in these games are encoded as game theoretic equilibrium concepts, e.g. Nash and coarse correlated equilibria. As directly computing an equilibrium is typically impractical, one often aims to design learning algorithms that iteratively converge to equilibria. A growing body of negative results casts doubt on this goal, from non-convergence to chaotic and even arbitrary behaviour. In this paper we add a strong negative result to this list: learning in games is Turing complete. Specifically, we prove Turing completeness of the replicator dynamic on matrix games, one of the simplest possible settings. Our results imply the undecicability of reachability problems for learning algorithms in games, a special case of which is determining equilibrium convergence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge