Gabriel P. Andrade
No-Regret Learning in Games is Turing Complete
Feb 24, 2022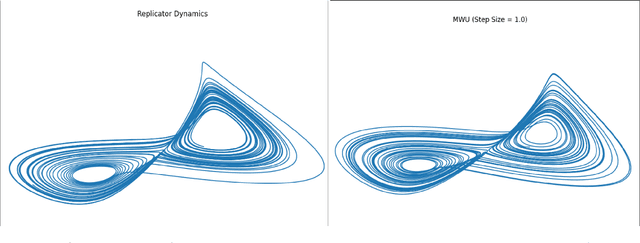
Abstract:Games are natural models for multi-agent machine learning settings, such as generative adversarial networks (GANs). The desirable outcomes from algorithmic interactions in these games are encoded as game theoretic equilibrium concepts, e.g. Nash and coarse correlated equilibria. As directly computing an equilibrium is typically impractical, one often aims to design learning algorithms that iteratively converge to equilibria. A growing body of negative results casts doubt on this goal, from non-convergence to chaotic and even arbitrary behaviour. In this paper we add a strong negative result to this list: learning in games is Turing complete. Specifically, we prove Turing completeness of the replicator dynamic on matrix games, one of the simplest possible settings. Our results imply the undecicability of reachability problems for learning algorithms in games, a special case of which is determining equilibrium convergence.
Learning in Matrix Games can be Arbitrarily Complex
Mar 05, 2021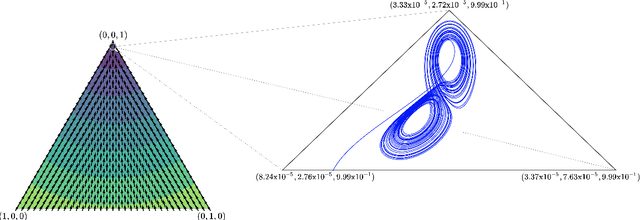
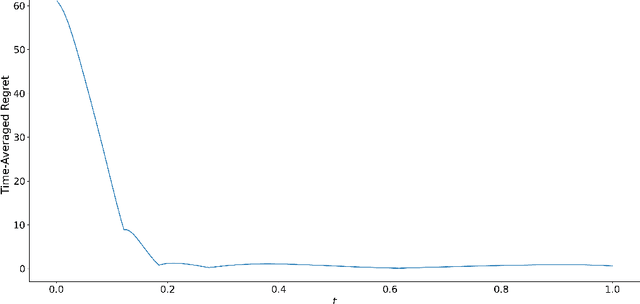
Abstract:A growing number of machine learning architectures, such as Generative Adversarial Networks, rely on the design of games which implement a desired functionality via a Nash equilibrium. In practice these games have an implicit complexity (e.g. from underlying datasets and the deep networks used) that makes directly computing a Nash equilibrium impractical or impossible. For this reason, numerous learning algorithms have been developed with the goal of iteratively converging to a Nash equilibrium. Unfortunately, the dynamics generated by the learning process can be very intricate and instances of training failure hard to interpret. In this paper we show that, in a strong sense, this dynamic complexity is inherent to games. Specifically, we prove that replicator dynamics, the continuous-time analogue of Multiplicative Weights Update, even when applied in a very restricted class of games -- known as finite matrix games -- is rich enough to be able to approximate arbitrary dynamical systems. Our results are positive in the sense that they show the nearly boundless dynamic modelling capabilities of current machine learning practices, but also negative in implying that these capabilities may come at the cost of interpretability. As a concrete example, we show how replicator dynamics can effectively reproduce the well-known strange attractor of Lonrenz dynamics (the "butterfly effect") while achieving no regret.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge