The no-free-lunch theorems of supervised learning

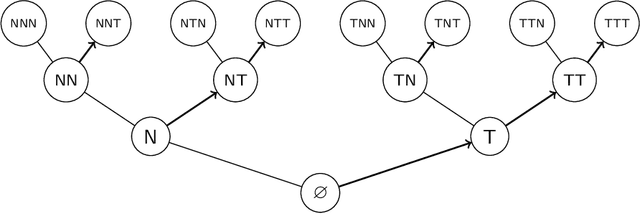
The no-free-lunch theorems promote a skeptical conclusion that all possible machine learning algorithms equally lack justification. But how could this leave room for a learning theory, that shows that some algorithms are better than others? Drawing parallels to the philosophy of induction, we point out that the no-free-lunch results presuppose a conception of learning algorithms as purely data-driven. On this conception, every algorithm must have an inherent inductive bias, that wants justification. We argue that many standard learning algorithms should rather be understood as model-dependent: in each application they also require for input a model, representing a bias. Generic algorithms themselves, they can be given a model-relative justification.

Fast Rates for General Unbounded Loss Functions: from ERM to Generalized Bayes

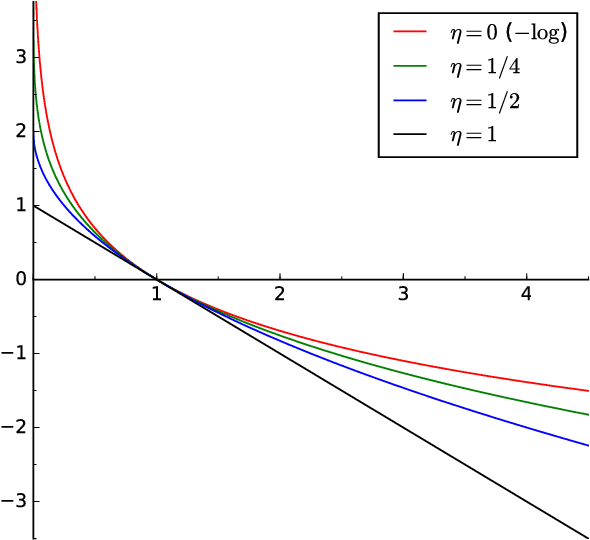
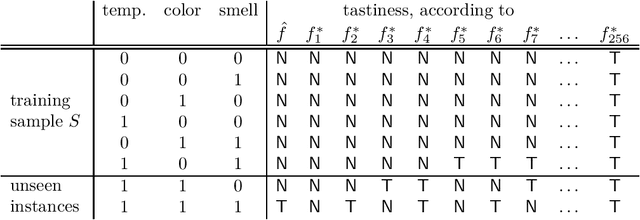
We present new excess risk bounds for general unbounded loss functions including log loss and squared loss, where the distribution of the losses may be heavy-tailed. The bounds hold for general estimators, but they are optimized when applied to $\eta$-generalized Bayesian, MDL, and empirical risk minimization estimators. In the case of log loss, the bounds imply convergence rates for generalized Bayesian inference under misspecification in terms of a generalization of the Hellinger metric as long as the learning rate $\eta$ is set correctly. For general loss functions, our bounds rely on two separate conditions: the $v$-GRIP (generalized reversed information projection) conditions, which control the lower tail of the excess loss; and the newly introduced witness condition, which controls the upper tail. The parameter $v$ in the $v$-GRIP conditions determines the achievable rate and is akin to the exponent in the Tsybakov margin condition and the Bernstein condition for bounded losses, which the $v$-GRIP conditions generalize; favorable $v$ in combination with small model complexity leads to $\tilde{O}(1/n)$ rates. The witness condition allows us to connect the excess risk to an 'annealed' version thereof, by which we generalize several previous results connecting Hellinger and R\'enyi divergence to KL divergence.

A Tight Excess Risk Bound via a Unified PAC-Bayesian-Rademacher-Shtarkov-MDL Complexity

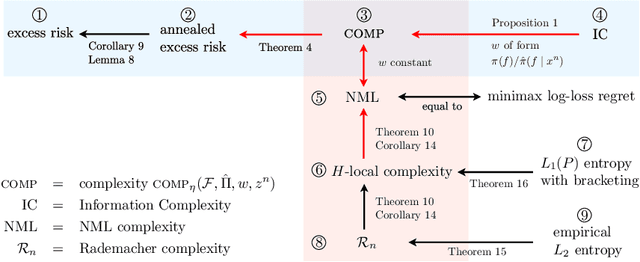
We present a novel notion of complexity that interpolates between and generalizes some classic existing complexity notions in learning theory: for estimators like empirical risk minimization (ERM) with arbitrary bounded losses, it is upper bounded in terms of data-independent Rademacher complexity; for generalized Bayesian estimators, it is upper bounded by the data-dependent information complexity (also known as stochastic or PAC-Bayesian, $\mathrm{KL}(\text{posterior} \operatorname{\|} \text{prior})$ complexity. For (penalized) ERM, the new complexity reduces to (generalized) normalized maximum likelihood (NML) complexity, i.e. a minimax log-loss individual-sequence regret. Our first main result bounds excess risk in terms of the new complexity. Our second main result links the new complexity via Rademacher complexity to $L_2(P)$ entropy, thereby generalizing earlier results of Opper, Haussler, Lugosi, and Cesa-Bianchi who did the log-loss case with $L_\infty$. Together, these results recover optimal bounds for VC- and large (polynomial entropy) classes, replacing localized Rademacher complexity by a simpler analysis which almost completely separates the two aspects that determine the achievable rates: 'easiness' (Bernstein) conditions and model complexity.

Fast rates in statistical and online learning

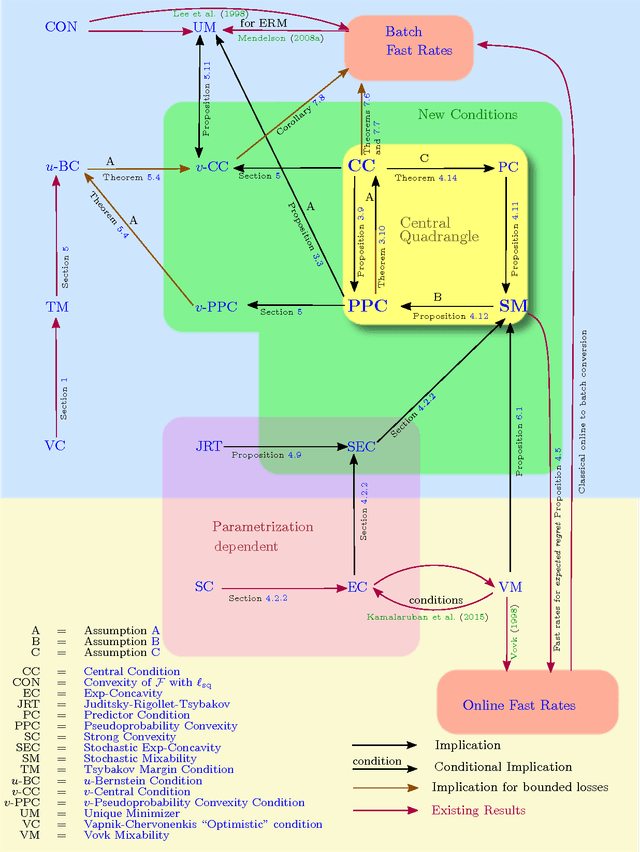
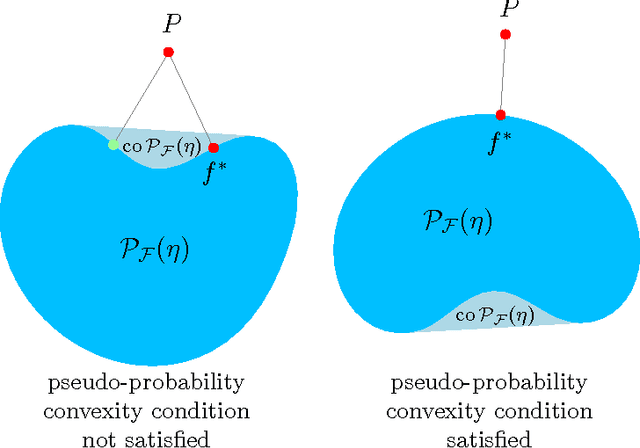
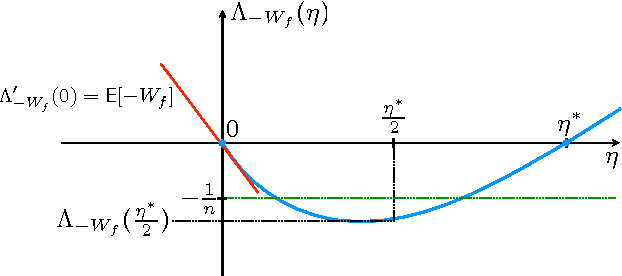
The speed with which a learning algorithm converges as it is presented with more data is a central problem in machine learning --- a fast rate of convergence means less data is needed for the same level of performance. The pursuit of fast rates in online and statistical learning has led to the discovery of many conditions in learning theory under which fast learning is possible. We show that most of these conditions are special cases of a single, unifying condition, that comes in two forms: the central condition for 'proper' learning algorithms that always output a hypothesis in the given model, and stochastic mixability for online algorithms that may make predictions outside of the model. We show that under surprisingly weak assumptions both conditions are, in a certain sense, equivalent. The central condition has a re-interpretation in terms of convexity of a set of pseudoprobabilities, linking it to density estimation under misspecification. For bounded losses, we show how the central condition enables a direct proof of fast rates and we prove its equivalence to the Bernstein condition, itself a generalization of the Tsybakov margin condition, both of which have played a central role in obtaining fast rates in statistical learning. Yet, while the Bernstein condition is two-sided, the central condition is one-sided, making it more suitable to deal with unbounded losses. In its stochastic mixability form, our condition generalizes both a stochastic exp-concavity condition identified by Juditsky, Rigollet and Tsybakov and Vovk's notion of mixability. Our unifying conditions thus provide a substantial step towards a characterization of fast rates in statistical learning, similar to how classical mixability characterizes constant regret in the sequential prediction with expert advice setting.

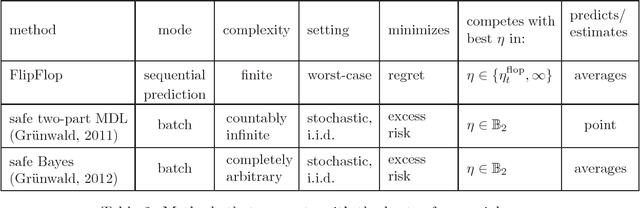
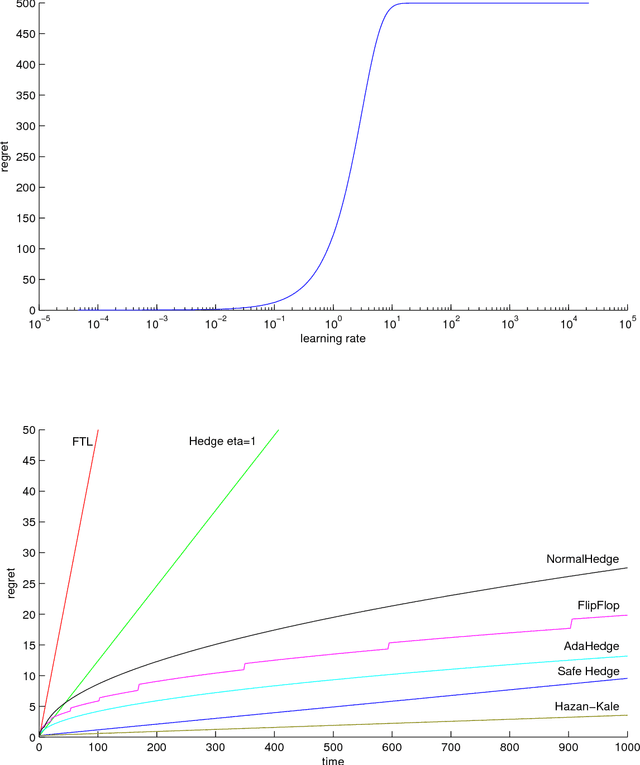
Follow the Leader If You Can, Hedge If You Must

Follow-the-Leader (FTL) is an intuitive sequential prediction strategy that guarantees constant regret in the stochastic setting, but has terrible performance for worst-case data. Other hedging strategies have better worst-case guarantees but may perform much worse than FTL if the data are not maximally adversarial. We introduce the FlipFlop algorithm, which is the first method that provably combines the best of both worlds. As part of our construction, we develop AdaHedge, which is a new way of dynamically tuning the learning rate in Hedge without using the doubling trick. AdaHedge refines a method by Cesa-Bianchi, Mansour and Stoltz (2007), yielding slightly improved worst-case guarantees. By interleaving AdaHedge and FTL, the FlipFlop algorithm achieves regret within a constant factor of the FTL regret, without sacrificing AdaHedge's worst-case guarantees. AdaHedge and FlipFlop do not need to know the range of the losses in advance; moreover, unlike earlier methods, both have the intuitive property that the issued weights are invariant under rescaling and translation of the losses. The losses are also allowed to be negative, in which case they may be interpreted as gains.