Statistical learning theory and Occam's razor: The argument from empirical risk minimization

This paper considers the epistemic justification for a simplicity preference in inductive inference that may be obtained from the machine learning framework of statistical learning theory. Uniting elements from both earlier arguments suggesting and rejecting such a justification, the paper spells out a qualified means-ends and model-relative justificatory argument, built on statistical learning theory's central mathematical learning guarantee for the method of empirical risk minimization.

On characterizations of learnability with computable learners

We study computable PAC (CPAC) learning as introduced by Agarwal et al. (2020). First, we consider the main open question of finding characterizations of proper and improper CPAC learning. We give a characterization of a closely related notion of strong CPAC learning, and we provide a negative answer to the open problem posed by Agarwal et al. (2021) whether all decidable PAC learnable classes are improperly CPAC learnable. Second, we consider undecidability of (computable) PAC learnability. We give a simple and general argument to exhibit such undecidability, and we initiate a study of the arithmetical complexity of learnability. We briefly discuss the relation to the undecidability result of Ben-David et al. (2019), that motivated the work of Agarwal et al.

The no-free-lunch theorems of supervised learning

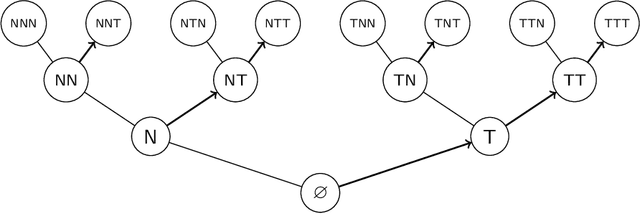
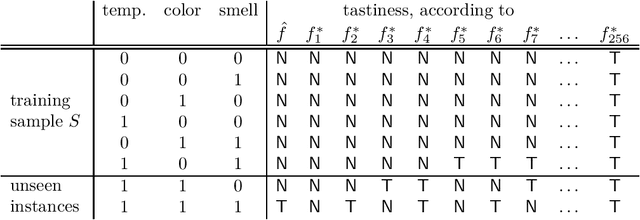
The no-free-lunch theorems promote a skeptical conclusion that all possible machine learning algorithms equally lack justification. But how could this leave room for a learning theory, that shows that some algorithms are better than others? Drawing parallels to the philosophy of induction, we point out that the no-free-lunch results presuppose a conception of learning algorithms as purely data-driven. On this conception, every algorithm must have an inherent inductive bias, that wants justification. We argue that many standard learning algorithms should rather be understood as model-dependent: in each application they also require for input a model, representing a bias. Generic algorithms themselves, they can be given a model-relative justification.