Fast Fair Regression via Efficient Approximations of Mutual Information

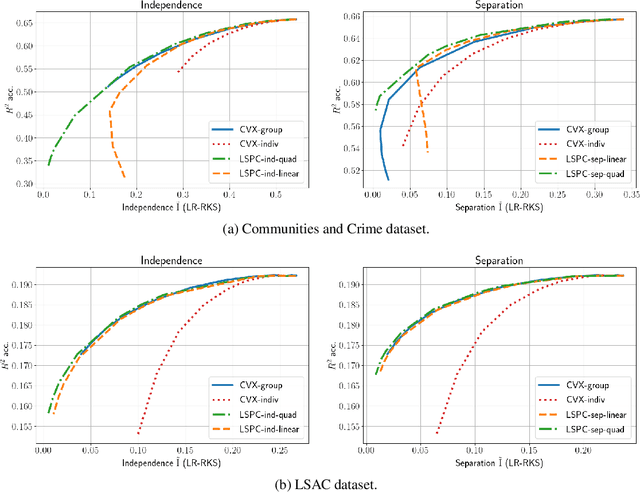
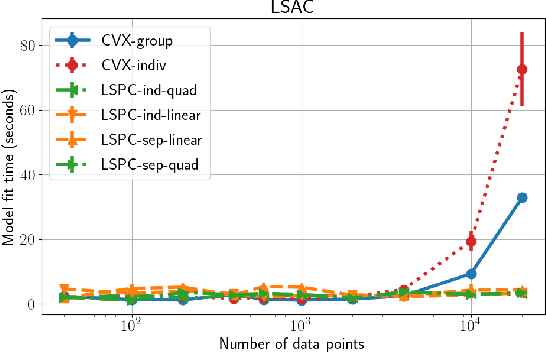
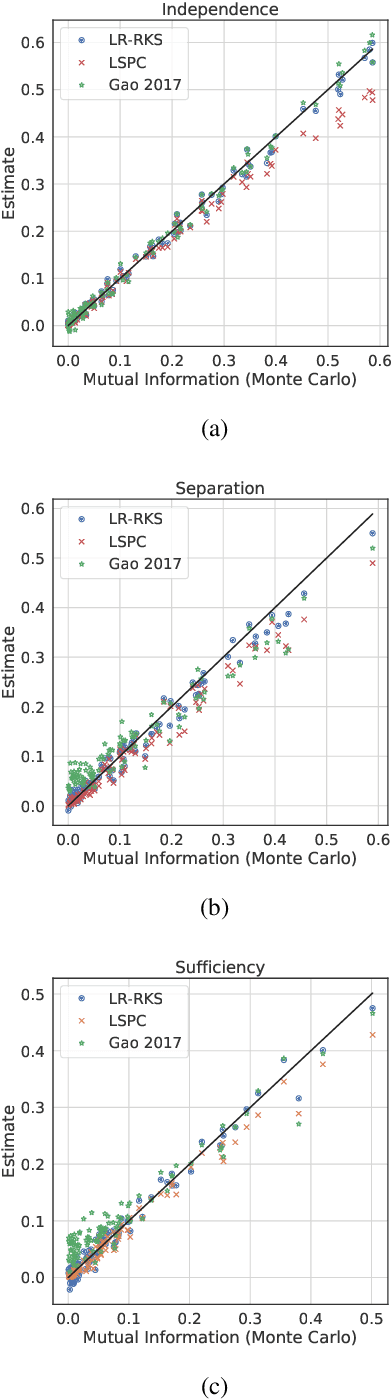
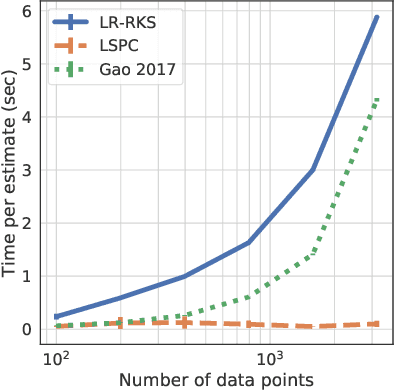
Most work in algorithmic fairness to date has focused on discrete outcomes, such as deciding whether to grant someone a loan or not. In these classification settings, group fairness criteria such as independence, separation and sufficiency can be measured directly by comparing rates of outcomes between subpopulations. Many important problems however require the prediction of a real-valued outcome, such as a risk score or insurance premium. In such regression settings, measuring group fairness criteria is computationally challenging, as it requires estimating information-theoretic divergences between conditional probability density functions. This paper introduces fast approximations of the independence, separation and sufficiency group fairness criteria for regression models from their (conditional) mutual information definitions, and uses such approximations as regularisers to enforce fairness within a regularised risk minimisation framework. Experiments in real-world datasets indicate that in spite of its superior computational efficiency our algorithm still displays state-of-the-art accuracy/fairness tradeoffs.

Causal inference with Bayes rule

The concept of causality has a controversial history. The question of whether it is possible to represent and address causal problems with probability theory, or if fundamentally new mathematics such as the do-calculus is required has been hotly debated, In this paper we demonstrate that, while it is critical to explicitly model our assumptions on the impact of intervening in a system, provided we do so, estimating causal effects can be done entirely within the standard Bayesian paradigm. The invariance assumptions underlying causal graphical models can be encoded in ordinary Probabilistic graphical models, allowing causal estimation with Bayesian statistics, equivalent to the do-calculus.

Replacing the do-calculus with Bayes rule

The concept of causality has a controversial history. The question of whether it is possible to represent and address causal problems with probability theory, or if fundamentally new mathematics such as the do calculus is required has been hotly debated, e.g. Pearl (2001) states "the building blocks of our scientific and everyday knowledge are elementary facts such as "mud does not cause rain" and "symptoms do not cause disease" and those facts, strangely enough, cannot be expressed in the vocabulary of probability calculus". This has lead to a dichotomy between advocates of causal graphical modeling and the do calculus, and researchers applying Bayesian methods. In this paper we demonstrate that, while it is critical to explicitly model our assumptions on the impact of intervening in a system, provided we do so, estimating causal effects can be done entirely within the standard Bayesian paradigm. The invariance assumptions underlying causal graphical models can be encoded in ordinary Probabilistic graphical models, allowing causal estimation with Bayesian statistics, equivalent to the do calculus. Elucidating the connections between these approaches is a key step toward enabling the insights provided by each to be combined to solve real problems.

A Primer on Causal Analysis

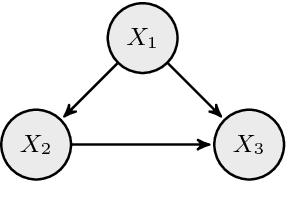
We provide a conceptual map to navigate causal analysis problems. Focusing on the case of discrete random variables, we consider the case of causal effect estimation from observational data. The presented approaches apply also to continuous variables, but the issue of estimation becomes more complex. We then introduce the four schools of thought for causal analysis

The Crossover Process: Learnability and Data Protection from Inference Attacks

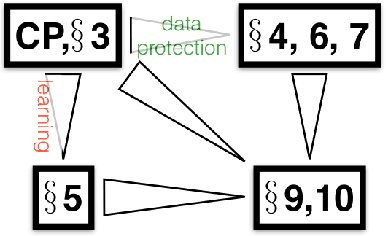
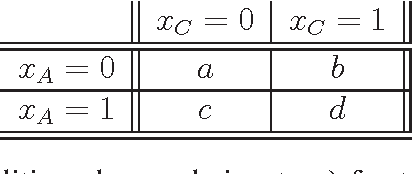
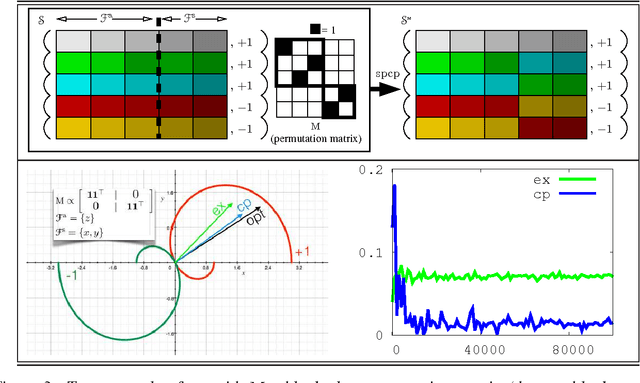
It is usual to consider data protection and learnability as conflicting objectives. This is not always the case: we show how to jointly control inference --- seen as the attack --- and learnability by a noise-free process that mixes training examples, the Crossover Process (cp). One key point is that the cp~is typically able to alter joint distributions without touching on marginals, nor altering the sufficient statistic for the class. In other words, it saves (and sometimes improves) generalization for supervised learning, but can alter the relationship between covariates --- and therefore fool measures of nonlinear independence and causal inference into misleading ad-hoc conclusions. For example, a cp~can increase / decrease odds ratios, bring fairness or break fairness, tamper with disparate impact, strengthen, weaken or reverse causal directions, change observed statistical measures of dependence. For each of these, we quantify changes brought by a cp, as well as its statistical impact on generalization abilities via a new complexity measure that we call the Rademacher cp~complexity. Experiments on a dozen readily available domains validate the theory.

Causal Bandits: Learning Good Interventions via Causal Inference

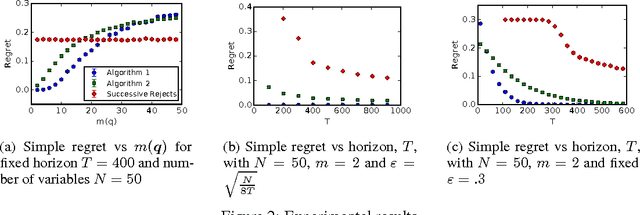
We study the problem of using causal models to improve the rate at which good interventions can be learned online in a stochastic environment. Our formalism combines multi-arm bandits and causal inference to model a novel type of bandit feedback that is not exploited by existing approaches. We propose a new algorithm that exploits the causal feedback and prove a bound on its simple regret that is strictly better (in all quantities) than algorithms that do not use the additional causal information.