Alistair Reid
Fast Fair Regression via Efficient Approximations of Mutual Information
Feb 14, 2020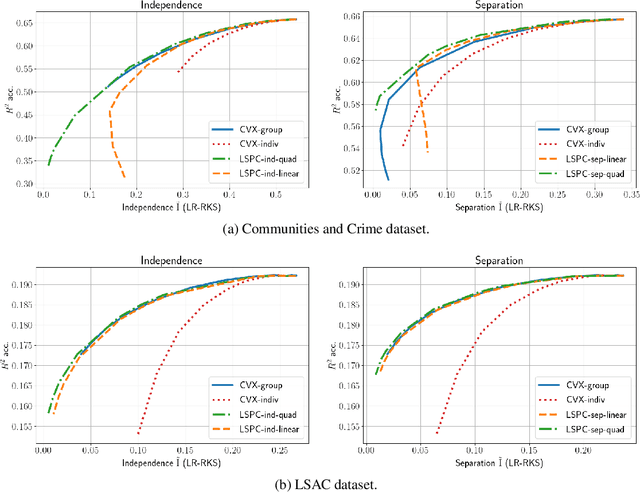
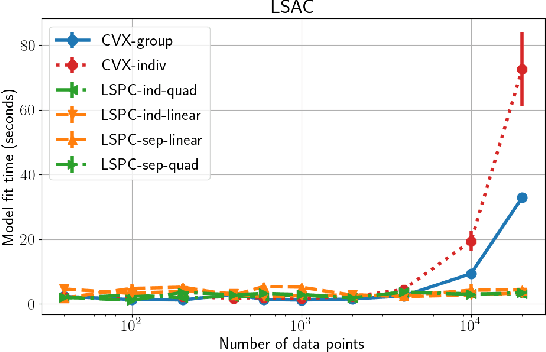
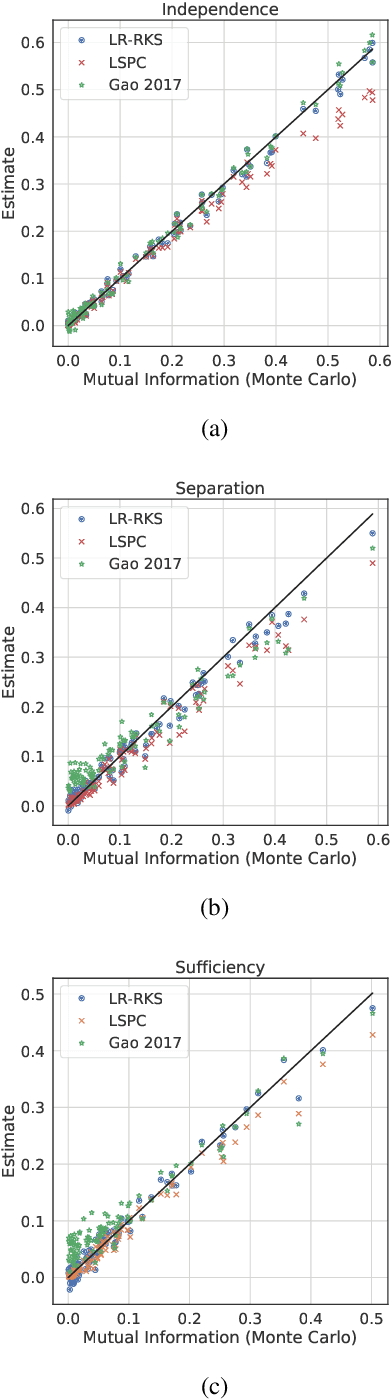
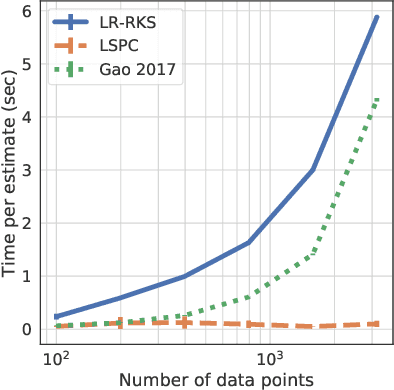
Abstract:Most work in algorithmic fairness to date has focused on discrete outcomes, such as deciding whether to grant someone a loan or not. In these classification settings, group fairness criteria such as independence, separation and sufficiency can be measured directly by comparing rates of outcomes between subpopulations. Many important problems however require the prediction of a real-valued outcome, such as a risk score or insurance premium. In such regression settings, measuring group fairness criteria is computationally challenging, as it requires estimating information-theoretic divergences between conditional probability density functions. This paper introduces fast approximations of the independence, separation and sufficiency group fairness criteria for regression models from their (conditional) mutual information definitions, and uses such approximations as regularisers to enforce fairness within a regularised risk minimisation framework. Experiments in real-world datasets indicate that in spite of its superior computational efficiency our algorithm still displays state-of-the-art accuracy/fairness tradeoffs.
Fairness Measures for Regression via Probabilistic Classification
Jan 16, 2020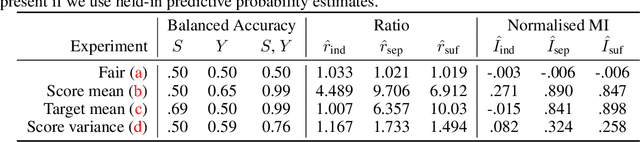
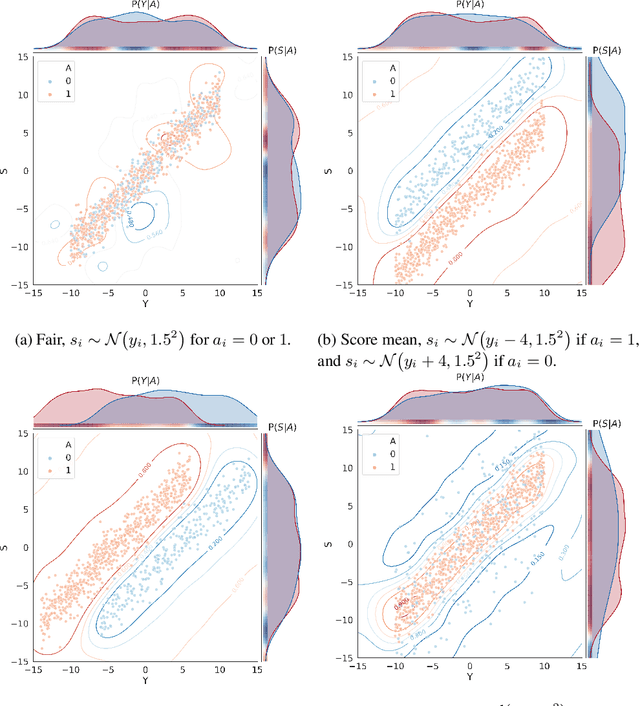
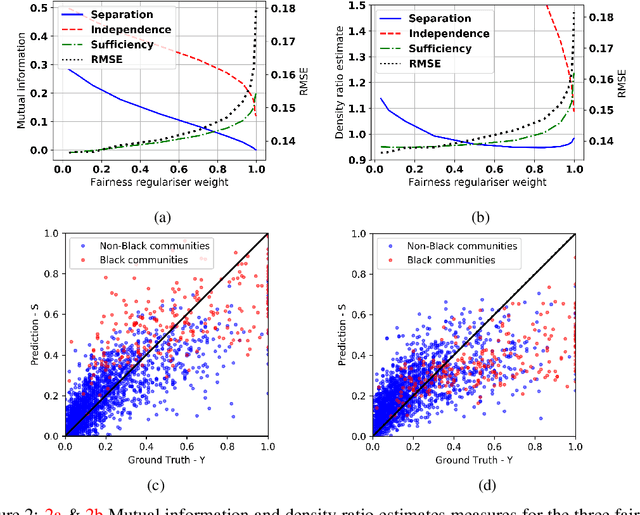
Abstract:Algorithmic fairness involves expressing notions such as equity, or reasonable treatment, as quantifiable measures that a machine learning algorithm can optimise. Most work in the literature to date has focused on classification problems where the prediction is categorical, such as accepting or rejecting a loan application. This is in part because classification fairness measures are easily computed by comparing the rates of outcomes, leading to behaviours such as ensuring that the same fraction of eligible men are selected as eligible women. But such measures are computationally difficult to generalise to the continuous regression setting for problems such as pricing, or allocating payments. The difficulty arises from estimating conditional densities (such as the probability density that a system will over-charge by a certain amount). For the regression setting we introduce tractable approximations of the independence, separation and sufficiency criteria by observing that they factorise as ratios of different conditional probabilities of the protected attributes. We introduce and train machine learning classifiers, distinct from the predictor, as a mechanism to estimate these probabilities from the data. This naturally leads to model agnostic, tractable approximations of the criteria, which we explore experimentally.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge