Tighter Variational Representations of f-Divergences via Restriction to Probability Measures

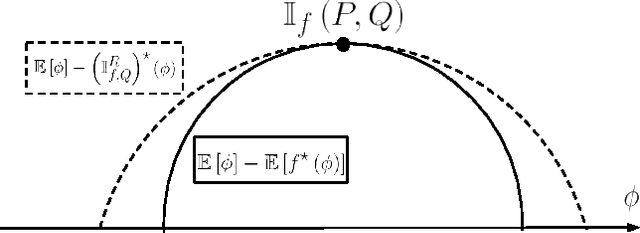
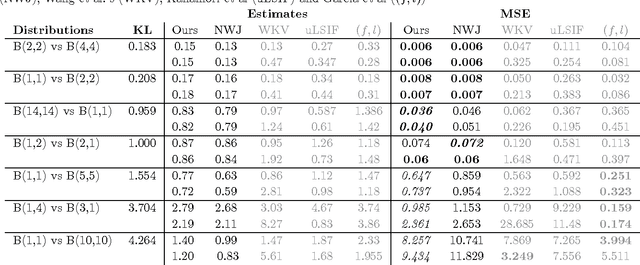
We show that the variational representations for f-divergences currently used in the literature can be tightened. This has implications to a number of methods recently proposed based on this representation. As an example application we use our tighter representation to derive a general f-divergence estimator based on two i.i.d. samples and derive the dual program for this estimator that performs well empirically. We also point out a connection between our estimator and MMD.

Scalable Inference for Latent Dirichlet Allocation

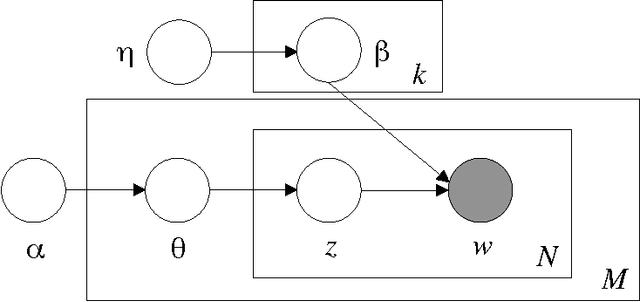
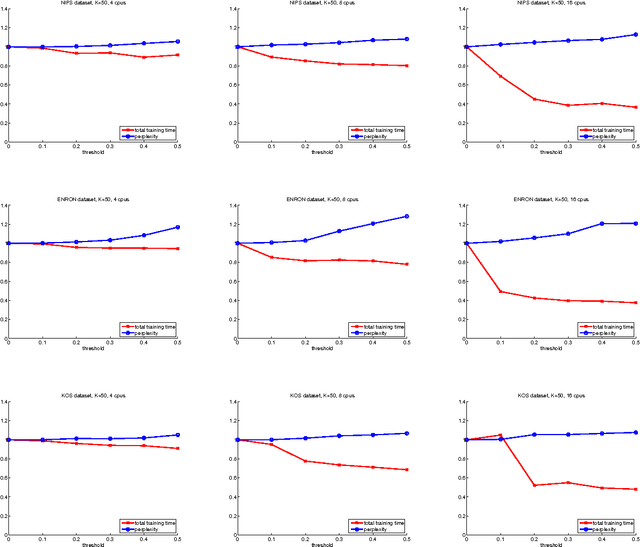
We investigate the problem of learning a topic model - the well-known Latent Dirichlet Allocation - in a distributed manner, using a cluster of C processors and dividing the corpus to be learned equally among them. We propose a simple approximated method that can be tuned, trading speed for accuracy according to the task at hand. Our approach is asynchronous, and therefore suitable for clusters of heterogenous machines.

Exponential Family Graph Matching and Ranking

We present a method for learning max-weight matching predictors in bipartite graphs. The method consists of performing maximum a posteriori estimation in exponential families with sufficient statistics that encode permutations and data features. Although inference is in general hard, we show that for one very relevant application - web page ranking - exact inference is efficient. For general model instances, an appropriate sampler is readily available. Contrary to existing max-margin matching models, our approach is statistically consistent and, in addition, experiments with increasing sample sizes indicate superior improvement over such models. We apply the method to graph matching in computer vision as well as to a standard benchmark dataset for learning web page ranking, in which we obtain state-of-the-art results, in particular improving on max-margin variants. The drawback of this method with respect to max-margin alternatives is its runtime for large graphs, which is comparatively high.