PSI Draft Specification

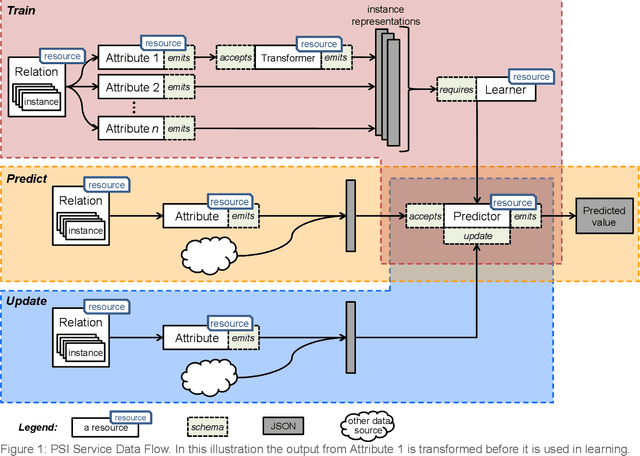
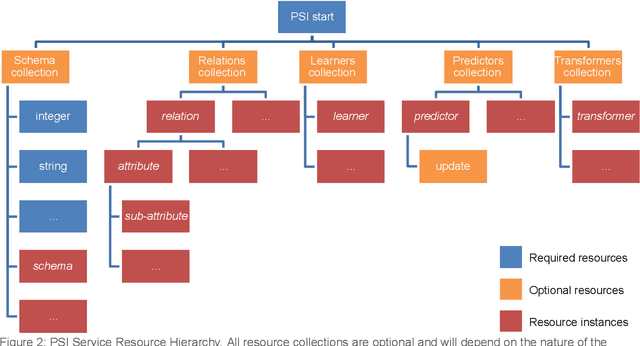
This document presents the draft specification for delivering machine learning services over HTTP, developed as part of the Protocols and Structures for Inference project, which concluded in 2013. It presents the motivation for providing machine learning as a service, followed by a description of the essential and optional components of such a service.

A Hybrid Loss for Multiclass and Structured Prediction

We propose a novel hybrid loss for multiclass and structured prediction problems that is a convex combination of a log loss for Conditional Random Fields (CRFs) and a multiclass hinge loss for Support Vector Machines (SVMs). We provide a sufficient condition for when the hybrid loss is Fisher consistent for classification. This condition depends on a measure of dominance between labels--specifically, the gap between the probabilities of the best label and the second best label. We also prove Fisher consistency is necessary for parametric consistency when learning models such as CRFs. We demonstrate empirically that the hybrid loss typically performs least as well as--and often better than--both of its constituent losses on a variety of tasks, such as human action recognition. In doing so we also provide an empirical comparison of the efficacy of probabilistic and margin based approaches to multiclass and structured prediction.

Tighter Variational Representations of f-Divergences via Restriction to Probability Measures

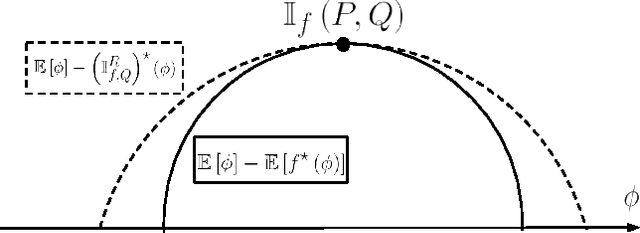
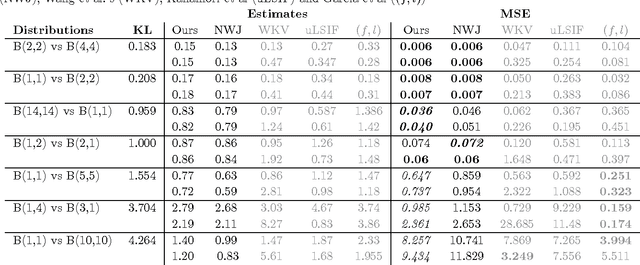
We show that the variational representations for f-divergences currently used in the literature can be tightened. This has implications to a number of methods recently proposed based on this representation. As an example application we use our tighter representation to derive a general f-divergence estimator based on two i.i.d. samples and derive the dual program for this estimator that performs well empirically. We also point out a connection between our estimator and MMD.

The Convexity and Design of Composite Multiclass Losses

We consider composite loss functions for multiclass prediction comprising a proper (i.e., Fisher-consistent) loss over probability distributions and an inverse link function. We establish conditions for their (strong) convexity and explore the implications. We also show how the separation of concerns afforded by using this composite representation allows for the design of families of losses with the same Bayes risk.