Safeguarding adaptive methods: global convergence of Barzilai-Borwein and other stepsize choices

Leveraging on recent advancements on adaptive methods for convex minimization problems, this paper provides a linesearch-free proximal gradient framework for globalizing the convergence of popular stepsize choices such as Barzilai-Borwein and one-dimensional Anderson acceleration. This framework can cope with problems in which the gradient of the differentiable function is merely locally H\"older continuous. Our analysis not only encompasses but also refines existing results upon which it builds. The theory is corroborated by numerical evidence that showcases the synergetic interplay between fast stepsize selections and adaptive methods.

Adaptive proximal gradient methods are universal without approximation

We show that adaptive proximal gradient methods for convex problems are not restricted to traditional Lipschitzian assumptions. Our analysis reveals that a class of linesearch-free methods is still convergent under mere local H\"older gradient continuity, covering in particular continuously differentiable semi-algebraic functions. To mitigate the lack of local Lipschitz continuity, popular approaches revolve around $\varepsilon$-oracles and/or linesearch procedures. In contrast, we exploit plain H\"older inequalities not entailing any approximation, all while retaining the linesearch-free nature of adaptive schemes. Furthermore, we prove full sequence convergence without prior knowledge of local H\"older constants nor of the order of H\"older continuity. In numerical experiments we present comparisons to baseline methods on diverse tasks from machine learning covering both the locally and the globally H\"older setting.

On the convergence of adaptive first order methods: proximal gradient and alternating minimization algorithms

Building upon recent works on linesearch-free adaptive proximal gradient methods, this paper proposes AdaPG$^{\pi,r}$, a framework that unifies and extends existing results by providing larger stepsize policies and improved lower bounds. Different choices of the parameters $\pi$ and $r$ are discussed and the efficacy of the resulting methods is demonstrated through numerical simulations. In an attempt to better understand the underlying theory, its convergence is established in a more general setting that allows for time-varying parameters. Finally, an adaptive alternating minimization algorithm is presented by exploring the dual setting. This algorithm not only incorporates additional adaptivity, but also expands its applicability beyond standard strongly convex settings.

Optimal Grid Layouts for Hybrid Offshore Assets in the North Sea under Different Market Designs

This work examines the Generation and Transmission Expansion (GATE) planning problem of offshore grids under different market clearing mechanisms: a Home Market Design (HMD), a zonal cleared Offshore Bidding Zone (zOBZ) and a nodal cleared Offshore Bidding Zone (nOBZ). It aims at answering two questions. 1) Is knowing the market structure a priori necessary for effective generation and transmission expansion planning? 2) Which market mechanism results in the highest overall social welfare? To this end a multi-period, stochastic GATE planning formulation is developed for both nodal and zonal market designs. The approach considers the costs and benefits among stake-holders of Hybrid Offshore Assets (HOA) as well as gross consumer surplus (GCS). The methodology is demonstrated on a North Sea test grid based on projects from the European Network of Transmission System Operators' (ENTSO-E) Ten Year Network Development Plan (TYNDP). An upper bound on potential social welfare in zonal market designs is calculated and it is concluded that from a generation and transmission perspective, planning under the assumption of an nOBZ results in the best risk adjusted return.

SPIRAL: A Superlinearly Convergent Incremental Proximal Algorithm for Nonconvex Finite Sum Minimization

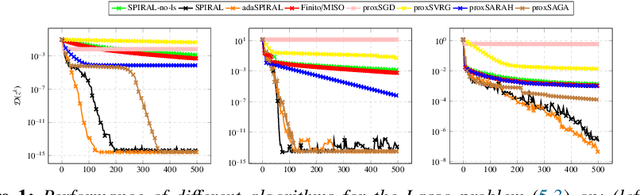
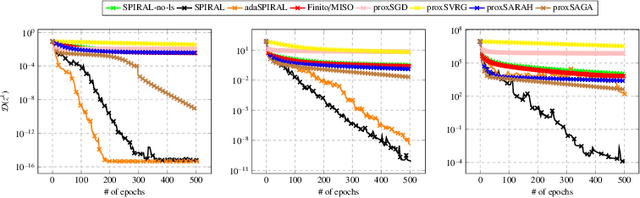
We introduce SPIRAL, a SuPerlinearly convergent Incremental pRoximal ALgorithm, for solving nonconvex regularized finite sum problems under a relative smoothness assumption. In the spirit of SVRG and SARAH, each iteration of SPIRAL consists of an inner and an outer loop. It combines incremental and full (proximal) gradient updates with a linesearch. It is shown that when using quasi-Newton directions, superlinear convergence is attained under mild assumptions at the limit points. More importantly, thanks to said linesearch, global convergence is ensured while it is shown that unit stepsize will be eventually always accepted. Simulation results on different convex, nonconvex, and non-Lipschitz differentiable problems show that our algorithm as well as its adaptive variant are competitive to the state of the art.

Lasry-Lions Envelopes and Nonconvex Optimization: A Homotopy Approach

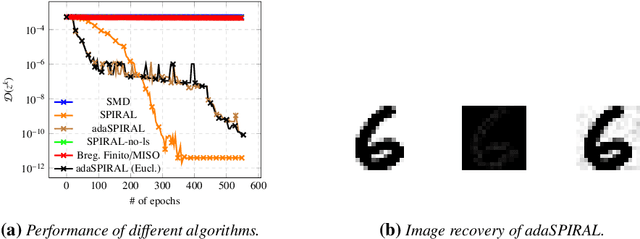
In large-scale optimization, the presence of nonsmooth and nonconvex terms in a given problem typically makes it hard to solve. A popular approach to address nonsmooth terms in convex optimization is to approximate them with their respective Moreau envelopes. In this work, we study the use of Lasry-Lions double envelopes to approximate nonsmooth terms that are also not convex. These envelopes are an extension of the Moreau ones but exhibit an additional smoothness property that makes them amenable to fast optimization algorithms. Lasry-Lions envelopes can also be seen as an "intermediate" between a given function and its convex envelope, and we make use of this property to develop a method that builds a sequence of approximate subproblems that are easier to solve than the original problem. We discuss convergence properties of this method when used to address composite minimization problems; additionally, based on a number of experiments, we discuss settings where it may be more useful than classical alternatives in two domains: signal decoding and spectral unmixing.