Miguel Simões
Algorithms based on operator-averaged operators
Dec 07, 2021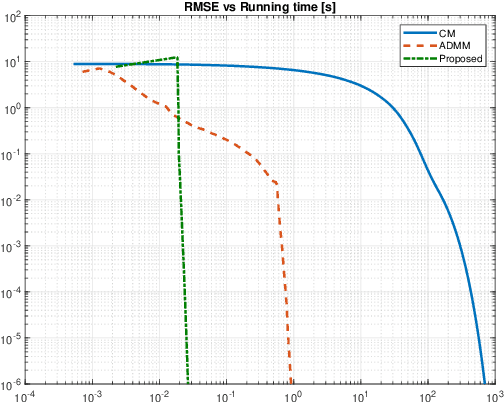

Abstract:A class of algorithms comprised by certain semismooth Newton and active-set methods is able to solve convex minimization problems involving sparsity-inducing regularizers very rapidly; the speed advantage of methods from this class is a consequence of their ability to benefit from the sparsity of the corresponding solutions by solving smaller inner problems than conventional methods. The convergence properties of such conventional methods (e.g., the forward-backward and the proximal-Newton ones) can be studied very elegantly under the framework of iterations of scalar-averaged operators - this is not the case for the aforementioned class. However, we show in this work that by instead considering operator-averaged operators, one can indeed study methods of that class, and also to derive algorithms outside of it that may be more convenient to implement than existing ones. Additionally, we present experiments whose results suggest that methods based on operator-averaged operators achieve substantially faster convergence than conventional ones.
Lasry-Lions Envelopes and Nonconvex Optimization: A Homotopy Approach
Mar 15, 2021

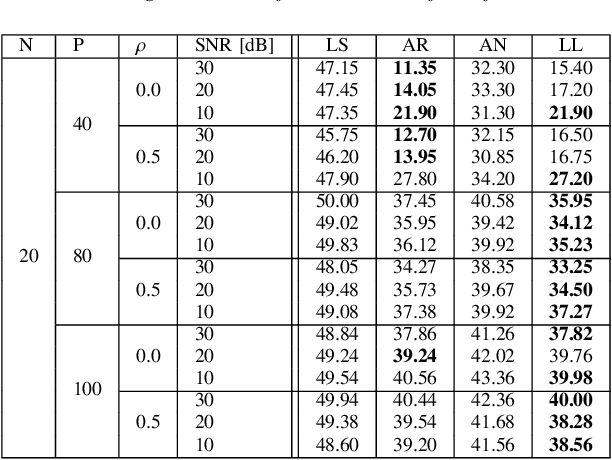

Abstract:In large-scale optimization, the presence of nonsmooth and nonconvex terms in a given problem typically makes it hard to solve. A popular approach to address nonsmooth terms in convex optimization is to approximate them with their respective Moreau envelopes. In this work, we study the use of Lasry-Lions double envelopes to approximate nonsmooth terms that are also not convex. These envelopes are an extension of the Moreau ones but exhibit an additional smoothness property that makes them amenable to fast optimization algorithms. Lasry-Lions envelopes can also be seen as an "intermediate" between a given function and its convex envelope, and we make use of this property to develop a method that builds a sequence of approximate subproblems that are easier to solve than the original problem. We discuss convergence properties of this method when used to address composite minimization problems; additionally, based on a number of experiments, we discuss settings where it may be more useful than classical alternatives in two domains: signal decoding and spectral unmixing.
An Extension of Averaged-Operator-Based Algorithms
Jun 12, 2018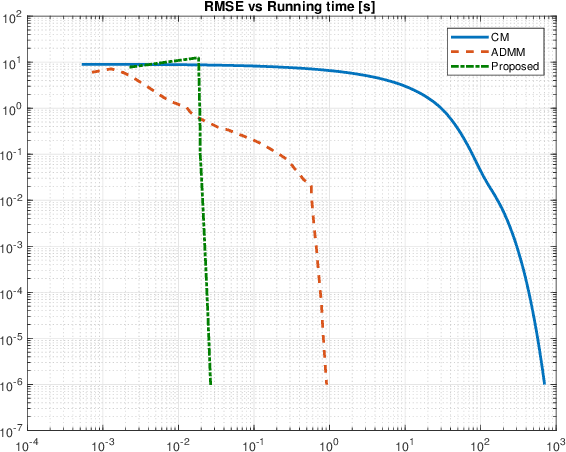
Abstract:Many of the algorithms used to solve minimization problems with sparsity-inducing regularizers are generic in the sense that they do not take into account the sparsity of the solution in any particular way. However, algorithms known as semismooth Newton are able to take advantage of this sparsity to accelerate their convergence. We show how to extend these algorithms in different directions, and study the convergence of the resulting algorithms by showing that they are a particular case of an extension of the well-known Krasnosel'ski\u{\i}--Mann scheme.
A Framework for Fast Image Deconvolution with Incomplete Observations
Aug 30, 2016

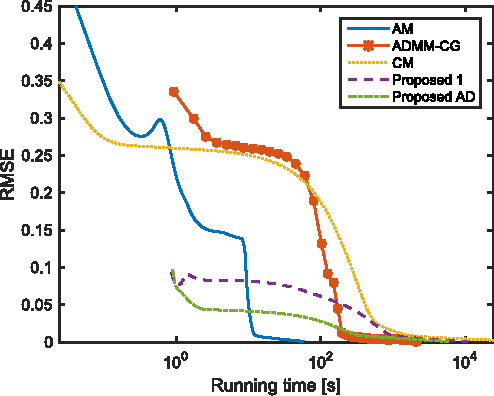

Abstract:In image deconvolution problems, the diagonalization of the underlying operators by means of the FFT usually yields very large speedups. When there are incomplete observations (e.g., in the case of unknown boundaries), standard deconvolution techniques normally involve non-diagonalizable operators, resulting in rather slow methods, or, otherwise, use inexact convolution models, resulting in the occurrence of artifacts in the enhanced images. In this paper, we propose a new deconvolution framework for images with incomplete observations that allows us to work with diagonalized convolution operators, and therefore is very fast. We iteratively alternate the estimation of the unknown pixels and of the deconvolved image, using, e.g., an FFT-based deconvolution method. This framework is an efficient, high-quality alternative to existing methods of dealing with the image boundaries, such as edge tapering. It can be used with any fast deconvolution method. We give an example in which a state-of-the-art method that assumes periodic boundary conditions is extended, through the use of this framework, to unknown boundary conditions. Furthermore, we propose a specific implementation of this framework, based on the alternating direction method of multipliers (ADMM). We provide a proof of convergence for the resulting algorithm, which can be seen as a "partial" ADMM, in which not all variables are dualized. We report experimental comparisons with other primal-dual methods, where the proposed one performed at the level of the state of the art. Four different kinds of applications were tested in the experiments: deconvolution, deconvolution with inpainting, superresolution, and demosaicing, all with unknown boundaries.
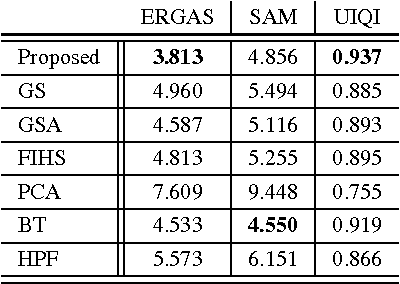
Hyperspectral pansharpening: a review
Apr 17, 2015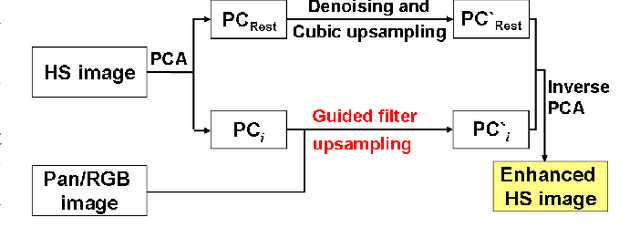
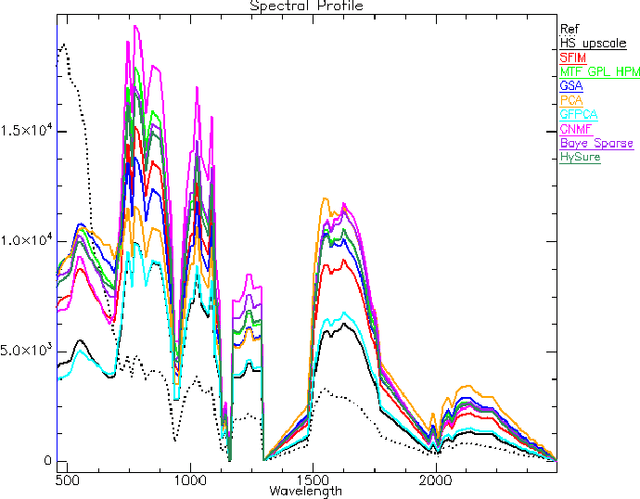
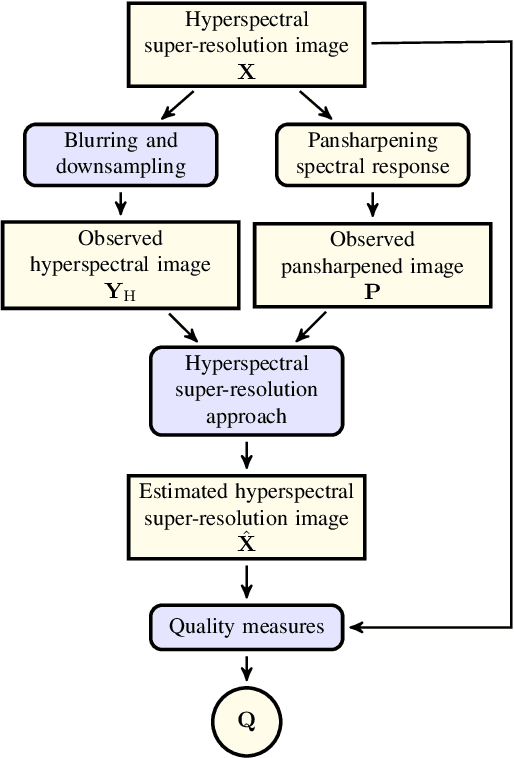

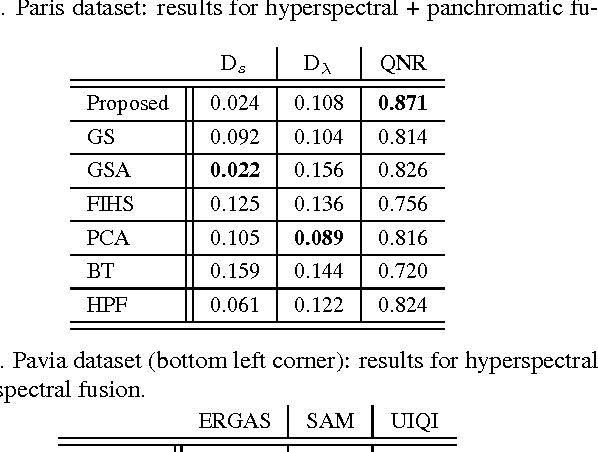
Abstract:Pansharpening aims at fusing a panchromatic image with a multispectral one, to generate an image with the high spatial resolution of the former and the high spectral resolution of the latter. In the last decade, many algorithms have been presented in the literature for pansharpening using multispectral data. With the increasing availability of hyperspectral systems, these methods are now being adapted to hyperspectral images. In this work, we compare new pansharpening techniques designed for hyperspectral data with some of the state of the art methods for multispectral pansharpening, which have been adapted for hyperspectral data. Eleven methods from different classes (component substitution, multiresolution analysis, hybrid, Bayesian and matrix factorization) are analyzed. These methods are applied to three datasets and their effectiveness and robustness are evaluated with widely used performance indicators. In addition, all the pansharpening techniques considered in this paper have been implemented in a MATLAB toolbox that is made available to the community.
A convex formulation for hyperspectral image superresolution via subspace-based regularization
Nov 14, 2014



Abstract:Hyperspectral remote sensing images (HSIs) usually have high spectral resolution and low spatial resolution. Conversely, multispectral images (MSIs) usually have low spectral and high spatial resolutions. The problem of inferring images which combine the high spectral and high spatial resolutions of HSIs and MSIs, respectively, is a data fusion problem that has been the focus of recent active research due to the increasing availability of HSIs and MSIs retrieved from the same geographical area. We formulate this problem as the minimization of a convex objective function containing two quadratic data-fitting terms and an edge-preserving regularizer. The data-fitting terms account for blur, different resolutions, and additive noise. The regularizer, a form of vector Total Variation, promotes piecewise-smooth solutions with discontinuities aligned across the hyperspectral bands. The downsampling operator accounting for the different spatial resolutions, the non-quadratic and non-smooth nature of the regularizer, and the very large size of the HSI to be estimated lead to a hard optimization problem. We deal with these difficulties by exploiting the fact that HSIs generally "live" in a low-dimensional subspace and by tailoring the Split Augmented Lagrangian Shrinkage Algorithm (SALSA), which is an instance of the Alternating Direction Method of Multipliers (ADMM), to this optimization problem, by means of a convenient variable splitting. The spatial blur and the spectral linear operators linked, respectively, with the HSI and MSI acquisition processes are also estimated, and we obtain an effective algorithm that outperforms the state-of-the-art, as illustrated in a series of experiments with simulated and real-life data.
Hyperspectral image superresolution: An edge-preserving convex formulation
Jun 10, 2014
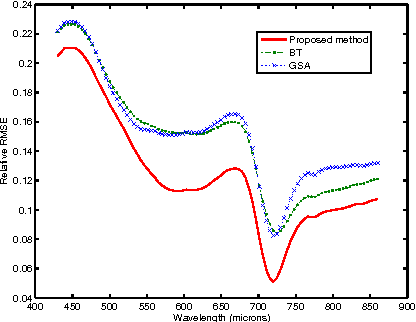
Abstract:Hyperspectral remote sensing images (HSIs) are characterized by having a low spatial resolution and a high spectral resolution, whereas multispectral images (MSIs) are characterized by low spectral and high spatial resolutions. These complementary characteristics have stimulated active research in the inference of images with high spatial and spectral resolutions from HSI-MSI pairs. In this paper, we formulate this data fusion problem as the minimization of a convex objective function containing two data-fitting terms and an edge-preserving regularizer. The data-fitting terms are quadratic and account for blur, different spatial resolutions, and additive noise; the regularizer, a form of vector Total Variation, promotes aligned discontinuities across the reconstructed hyperspectral bands. The optimization described above is rather hard, owing to its non-diagonalizable linear operators, to the non-quadratic and non-smooth nature of the regularizer, and to the very large size of the image to be inferred. We tackle these difficulties by tailoring the Split Augmented Lagrangian Shrinkage Algorithm (SALSA)---an instance of the Alternating Direction Method of Multipliers (ADMM)---to this optimization problem. By using a convenient variable splitting and by exploiting the fact that HSIs generally "live" in a low-dimensional subspace, we obtain an effective algorithm that yields state-of-the-art results, as illustrated by experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge