Bayesian Optimization from Human Feedback: Near-Optimal Regret Bounds

Bayesian optimization (BO) with preference-based feedback has recently garnered significant attention due to its emerging applications. We refer to this problem as Bayesian Optimization from Human Feedback (BOHF), which differs from conventional BO by learning the best actions from a reduced feedback model, where only the preference between two actions is revealed to the learner at each time step. The objective is to identify the best action using a limited number of preference queries, typically obtained through costly human feedback. Existing work, which adopts the Bradley-Terry-Luce (BTL) feedback model, provides regret bounds for the performance of several algorithms. In this work, within the same framework we develop tighter performance guarantees. Specifically, we derive regret bounds of $\tilde{\mathcal{O}}(\sqrt{\Gamma(T)T})$, where $\Gamma(T)$ represents the maximum information gain$\unicode{x2014}$a kernel-specific complexity term$\unicode{x2014}$and $T$ is the number of queries. Our results significantly improve upon existing bounds. Notably, for common kernels, we show that the order-optimal sample complexities of conventional BO$\unicode{x2014}$achieved with richer feedback models$\unicode{x2014}$are recovered. In other words, the same number of preferential samples as scalar-valued samples is sufficient to find a nearly optimal solution.

Near-Optimal Sample Complexity in Reward-Free Kernel-Based Reinforcement Learning

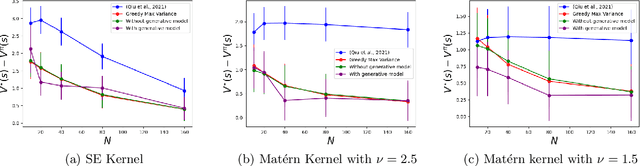
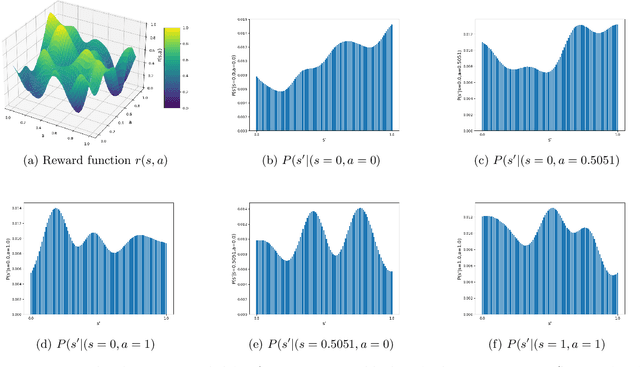
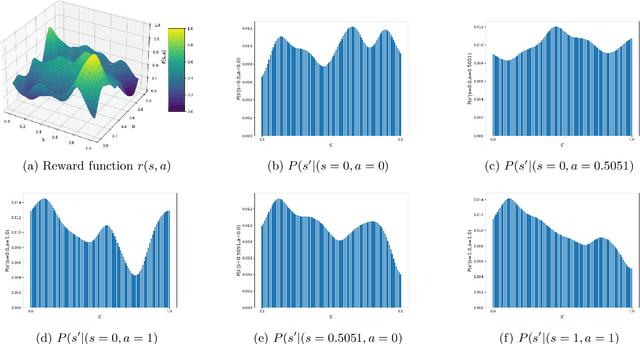
Reinforcement Learning (RL) problems are being considered under increasingly more complex structures. While tabular and linear models have been thoroughly explored, the analytical study of RL under nonlinear function approximation, especially kernel-based models, has recently gained traction for their strong representational capacity and theoretical tractability. In this context, we examine the question of statistical efficiency in kernel-based RL within the reward-free RL framework, specifically asking: how many samples are required to design a near-optimal policy? Existing work addresses this question under restrictive assumptions about the class of kernel functions. We first explore this question by assuming a generative model, then relax this assumption at the cost of increasing the sample complexity by a factor of H, the length of the episode. We tackle this fundamental problem using a broad class of kernels and a simpler algorithm compared to prior work. Our approach derives new confidence intervals for kernel ridge regression, specific to our RL setting, which may be of broader applicability. We further validate our theoretical findings through simulations.

Efficient Model Compression Techniques with FishLeg

In many domains, the most successful AI models tend to be the largest, indeed often too large to be handled by AI players with limited computational resources. To mitigate this, a number of compression methods have been developed, including methods that prune the network down to high sparsity whilst retaining performance. The best-performing pruning techniques are often those that use second-order curvature information (such as an estimate of the Fisher information matrix) to score the importance of each weight and to predict the optimal compensation for weight deletion. However, these methods are difficult to scale to high-dimensional parameter spaces without making heavy approximations. Here, we propose the FishLeg surgeon (FLS), a new second-order pruning method based on the Fisher-Legendre (FishLeg) optimizer. At the heart of FishLeg is a meta-learning approach to amortising the action of the inverse FIM, which brings a number of advantages. Firstly, the parameterisation enables the use of flexible tensor factorisation techniques to improve computational and memory efficiency without sacrificing much accuracy, alleviating challenges associated with scalability of most second-order pruning methods. Secondly, directly estimating the inverse FIM leads to less sensitivity to the amplification of stochasticity during inversion, thereby resulting in more precise estimates. Thirdly, our approach also allows for progressive assimilation of the curvature into the parameterisation. In the gradual pruning regime, this results in a more efficient estimate refinement as opposed to re-estimation. We find that FishLeg achieves higher or comparable performance against two common baselines in the area, most notably in the high sparsity regime when considering a ResNet18 model on CIFAR-10 (84% accuracy at 95% sparsity vs 60% for OBS) and TinyIM (53% accuracy at 80% sparsity vs 48% for OBS).

Exact, Tractable Gauss-Newton Optimization in Deep Reversible Architectures Reveal Poor Generalization

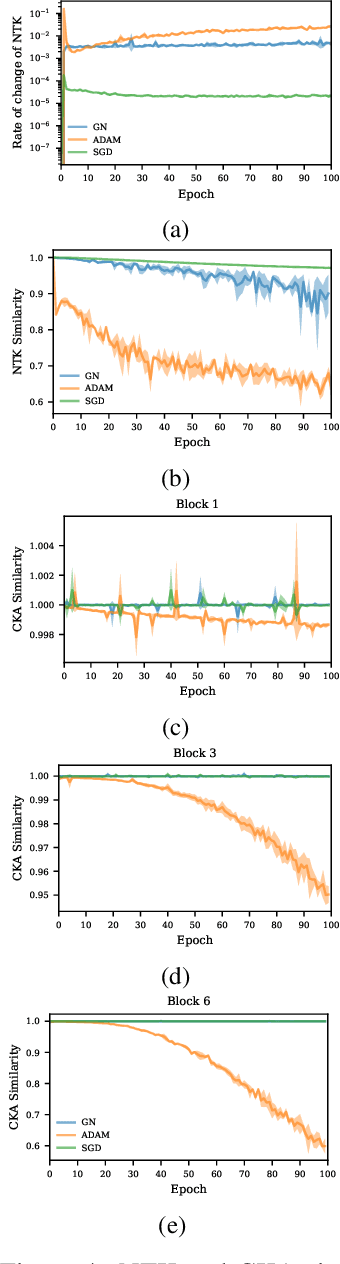
Second-order optimization has been shown to accelerate the training of deep neural networks in many applications, often yielding faster progress per iteration on the training loss compared to first-order optimizers. However, the generalization properties of second-order methods are still being debated. Theoretical investigations have proved difficult to carry out outside the tractable settings of heavily simplified model classes -- thus, the relevance of existing theories to practical deep learning applications remains unclear. Similarly, empirical studies in large-scale models and real datasets are significantly confounded by the necessity to approximate second-order updates in practice. It is often unclear whether the observed generalization behaviour arises specifically from the second-order nature of the parameter updates, or instead reflects the specific structured (e.g.\ Kronecker) approximations used or any damping-based interpolation towards first-order updates. Here, we show for the first time that exact Gauss-Newton (GN) updates take on a tractable form in a class of deep reversible architectures that are sufficiently expressive to be meaningfully applied to common benchmark datasets. We exploit this novel setting to study the training and generalization properties of the GN optimizer. We find that exact GN generalizes poorly. In the mini-batch training setting, this manifests as rapidly saturating progress even on the \emph{training} loss, with parameter updates found to overfit each mini-batchatch without producing the features that would support generalization to other mini-batches. We show that our experiments run in the ``lazy'' regime, in which the neural tangent kernel (NTK) changes very little during the course of training. This behaviour is associated with having no significant changes in neural representations, explaining the lack of generalization.

Score Normalization for a Faster Diffusion Exponential Integrator Sampler

Recently, Zhang et al. have proposed the Diffusion Exponential Integrator Sampler (DEIS) for fast generation of samples from Diffusion Models. It leverages the semi-linear nature of the probability flow ordinary differential equation (ODE) in order to greatly reduce integration error and improve generation quality at low numbers of function evaluations (NFEs). Key to this approach is the score function reparameterisation, which reduces the integration error incurred from using a fixed score function estimate over each integration step. The original authors use the default parameterisation used by models trained for noise prediction -- multiply the score by the standard deviation of the conditional forward noising distribution. We find that although the mean absolute value of this score parameterisation is close to constant for a large portion of the reverse sampling process, it changes rapidly at the end of sampling. As a simple fix, we propose to instead reparameterise the score (at inference) by dividing it by the average absolute value of previous score estimates at that time step collected from offline high NFE generations. We find that our score normalisation (DEIS-SN) consistently improves FID compared to vanilla DEIS, showing an improvement at 10 NFEs from 6.44 to 5.57 on CIFAR-10 and from 5.9 to 4.95 on LSUN-Church 64x64. Our code is available at https://github.com/mtkresearch/Diffusion-DEIS-SN

Generative Diffusion Models for Radio Wireless Channel Modelling and Sampling

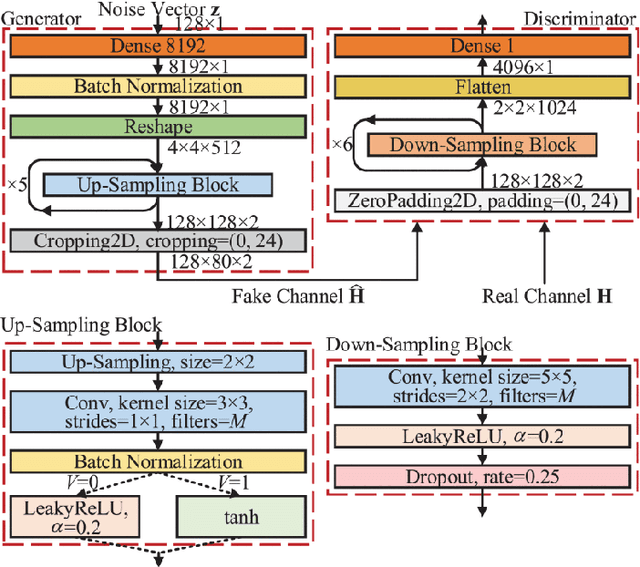
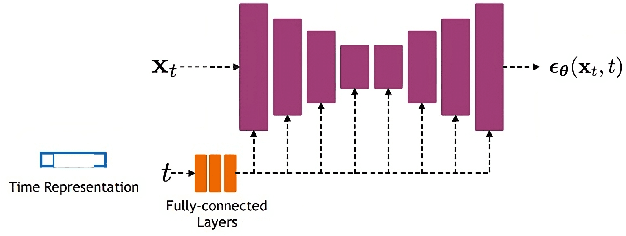
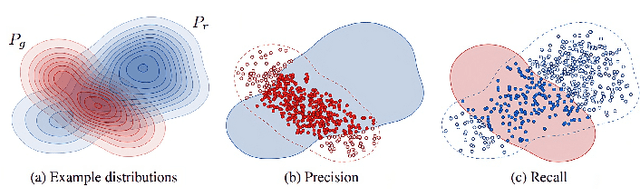
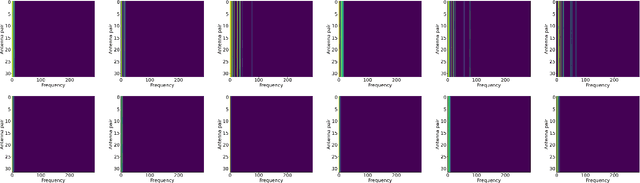
Channel modelling is essential to designing modern wireless communication systems. The increasing complexity of channel modelling and the cost of collecting high-quality wireless channel data have become major challenges. In this paper, we propose a diffusion model based channel sampling approach for rapidly synthesizing channel realizations from limited data. We use a diffusion model with a U Net based architecture operating in the frequency space domain. To evaluate how well the proposed model reproduces the true distribution of channels in the training dataset, two evaluation metrics are used: $i)$ the approximate $2$-Wasserstein distance between real and generated distributions of the normalized power spectrum in the antenna and frequency domains and $ii)$ precision and recall metric for distributions. We show that, compared to existing GAN based approaches which suffer from mode collapse and unstable training, our diffusion based approach trains stably and generates diverse and high-fidelity samples from the true channel distribution. We also show that we can pretrain the model on a simulated urban macro-cellular channel dataset and fine-tune it on a smaller, out-of-distribution urban micro-cellular dataset, therefore showing that it is feasible to model real world channels using limited data with this approach.

Image generation with shortest path diffusion

The field of image generation has made significant progress thanks to the introduction of Diffusion Models, which learn to progressively reverse a given image corruption. Recently, a few studies introduced alternative ways of corrupting images in Diffusion Models, with an emphasis on blurring. However, these studies are purely empirical and it remains unclear what is the optimal procedure for corrupting an image. In this work, we hypothesize that the optimal procedure minimizes the length of the path taken when corrupting an image towards a given final state. We propose the Fisher metric for the path length, measured in the space of probability distributions. We compute the shortest path according to this metric, and we show that it corresponds to a combination of image sharpening, rather than blurring, and noise deblurring. While the corruption was chosen arbitrarily in previous work, our Shortest Path Diffusion (SPD) determines uniquely the entire spatiotemporal structure of the corruption. We show that SPD improves on strong baselines without any hyperparameter tuning, and outperforms all previous Diffusion Models based on image blurring. Furthermore, any small deviation from the shortest path leads to worse performance, suggesting that SPD provides the optimal procedure to corrupt images. Our work sheds new light on observations made in recent works and provides a new approach to improve diffusion models on images and other types of data.

Sample Complexity of Kernel-Based Q-Learning

Modern reinforcement learning (RL) often faces an enormous state-action space. Existing analytical results are typically for settings with a small number of state-actions, or simple models such as linearly modeled Q-functions. To derive statistically efficient RL policies handling large state-action spaces, with more general Q-functions, some recent works have considered nonlinear function approximation using kernel ridge regression. In this work, we derive sample complexities for kernel based Q-learning when a generative model exists. We propose a nonparametric Q-learning algorithm which finds an $\epsilon$-optimal policy in an arbitrarily large scale discounted MDP. The sample complexity of the proposed algorithm is order optimal with respect to $\epsilon$ and the complexity of the kernel (in terms of its information gain). To the best of our knowledge, this is the first result showing a finite sample complexity under such a general model.

Delayed Feedback in Kernel Bandits

Black box optimisation of an unknown function from expensive and noisy evaluations is a ubiquitous problem in machine learning, academic research and industrial production. An abstraction of the problem can be formulated as a kernel based bandit problem (also known as Bayesian optimisation), where a learner aims at optimising a kernelized function through sequential noisy observations. The existing work predominantly assumes feedback is immediately available; an assumption which fails in many real world situations, including recommendation systems, clinical trials and hyperparameter tuning. We consider a kernel bandit problem under stochastically delayed feedback, and propose an algorithm with $\tilde{\mathcal{O}}(\sqrt{\Gamma_k(T)T}+\mathbb{E}[\tau])$ regret, where $T$ is the number of time steps, $\Gamma_k(T)$ is the maximum information gain of the kernel with $T$ observations, and $\tau$ is the delay random variable. This represents a significant improvement over the state of the art regret bound of $\tilde{\mathcal{O}}(\Gamma_k(T)\sqrt{T}+\mathbb{E}[\tau]\Gamma_k(T))$ reported in Verma et al. (2022). In particular, for very non-smooth kernels, the information gain grows almost linearly in time, trivializing the existing results. We also validate our theoretical results with simulations.

Improved Convergence Rates for Sparse Approximation Methods in Kernel-Based Learning

Kernel-based models such as kernel ridge regression and Gaussian processes are ubiquitous in machine learning applications for regression and optimization. It is well known that a serious downside for kernel-based models is the high computational cost; given a dataset of $n$ samples, the cost grows as $\mathcal{O}(n^3)$. Existing sparse approximation methods can yield a significant reduction in the computational cost, effectively reducing the real world cost down to as low as $\mathcal{O}(n)$ in certain cases. Despite this remarkable empirical success, significant gaps remain in the existing results for the analytical confidence bounds on the error due to approximation. In this work, we provide novel confidence intervals for the Nystr\"om method and the sparse variational Gaussian processes approximation method. Our confidence intervals lead to improved error bounds in both regression and optimization. We establish these confidence intervals using novel interpretations of the approximate (surrogate) posterior variance of the models.