Exact, Tractable Gauss-Newton Optimization in Deep Reversible Architectures Reveal Poor Generalization

Second-order optimization has been shown to accelerate the training of deep neural networks in many applications, often yielding faster progress per iteration on the training loss compared to first-order optimizers. However, the generalization properties of second-order methods are still being debated. Theoretical investigations have proved difficult to carry out outside the tractable settings of heavily simplified model classes -- thus, the relevance of existing theories to practical deep learning applications remains unclear. Similarly, empirical studies in large-scale models and real datasets are significantly confounded by the necessity to approximate second-order updates in practice. It is often unclear whether the observed generalization behaviour arises specifically from the second-order nature of the parameter updates, or instead reflects the specific structured (e.g.\ Kronecker) approximations used or any damping-based interpolation towards first-order updates. Here, we show for the first time that exact Gauss-Newton (GN) updates take on a tractable form in a class of deep reversible architectures that are sufficiently expressive to be meaningfully applied to common benchmark datasets. We exploit this novel setting to study the training and generalization properties of the GN optimizer. We find that exact GN generalizes poorly. In the mini-batch training setting, this manifests as rapidly saturating progress even on the \emph{training} loss, with parameter updates found to overfit each mini-batchatch without producing the features that would support generalization to other mini-batches. We show that our experiments run in the ``lazy'' regime, in which the neural tangent kernel (NTK) changes very little during the course of training. This behaviour is associated with having no significant changes in neural representations, explaining the lack of generalization.

Efficient Sampling for Data-Driven Frequency Stability Constraint via Forward-Mode Automatic Differentiation

Encoding frequency stability constraints in the operation problem is challenging due to its complex dynamics. Recently, data-driven approaches have been proposed to learn the stability criteria offline with the trained model embedded as a constraint of online optimization. However, random sampling of stationary operation points is less efficient in generating balanced stable and unstable samples. Meanwhile, the performance of such a model is strongly dependent on the quality of the training dataset. Observing this research gap, we propose a gradient-based data generation method via forward-mode automatic differentiation. In this method, the original dynamic system is augmented with new states that represent the dynamic of sensitivities of the original states, which can be solved by invoking any ODE solver for a single time. To compensate for the contradiction between the gradient of various frequency stability criteria, gradient surgery is proposed by projecting the gradient on the normal plane of the other. In the end, we demonstrate the superior performance of the proposed sampling algorithm, compared with the unrolling differentiation and finite difference. All codes are available at https://github.com/xuwkk/frequency_sample_ad.

E2E-AT: A Unified Framework for Tackling Uncertainty in Task-aware End-to-end Learning

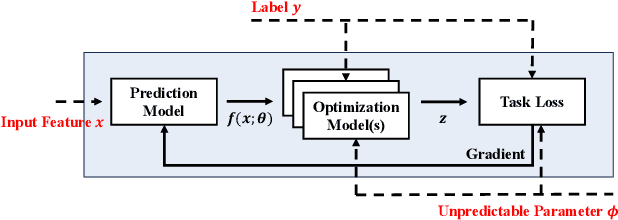
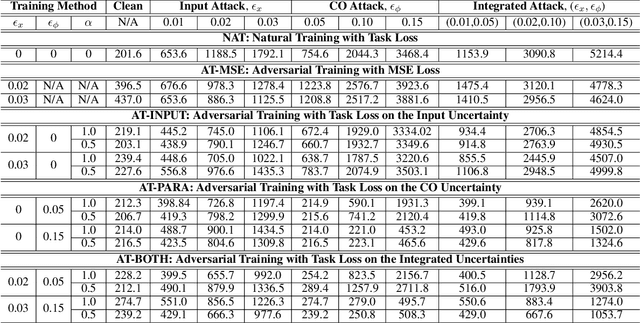
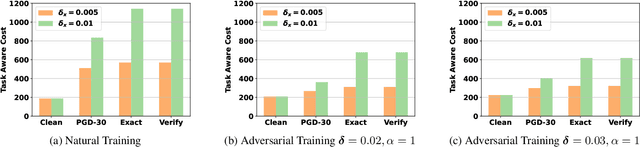
Successful machine learning involves a complete pipeline of data, model, and downstream applications. Instead of treating them separately, there has been a prominent increase of attention within the constrained optimization (CO) and machine learning (ML) communities towards combining prediction and optimization models. The so-called end-to-end (E2E) learning captures the task-based objective for which they will be used for decision making. Although a large variety of E2E algorithms have been presented, it has not been fully investigated how to systematically address uncertainties involved in such models. Most of the existing work considers the uncertainties of ML in the input space and improves robustness through adversarial training. We extend this idea to E2E learning and prove that there is a robustness certification procedure by solving augmented integer programming. Furthermore, we show that neglecting the uncertainty of COs during training causes a new trigger for generalization errors. To include all these components, we propose a unified framework that covers the uncertainties emerging in both the input feature space of the ML models and the COs. The framework is described as a robust optimization problem and is practically solved via end-to-end adversarial training (E2E-AT). Finally, the performance of E2E-AT is evaluated by a real-world end-to-end power system operation problem, including load forecasting and sequential scheduling tasks.

Task-Aware Machine Unlearning and Its Application in Load Forecasting

Data privacy and security have become a non-negligible factor in load forecasting. Previous researches mainly focus on training stage enhancement. However, once the model is trained and deployed, it may need to `forget' (i.e., remove the impact of) part of training data if the data is found to be malicious or as requested by the data owner. This paper introduces machine unlearning algorithm which is specifically designed to remove the influence of part of the original dataset on an already trained forecaster. However, direct unlearning inevitably degrades the model generalization ability. To balance between unlearning completeness and performance degradation, a performance-aware algorithm is proposed by evaluating the sensitivity of local model parameter change using influence function and sample re-weighting. Moreover, we observe that the statistic criterion cannot fully reflect the operation cost of down-stream tasks. Therefore, a task-aware machine unlearning is proposed whose objective is a tri-level optimization with dispatch and redispatch problems considered. We theoretically prove the existence of the gradient of such objective, which is key to re-weighting the remaining samples. We test the unlearning algorithms on linear and neural network load forecasters with realistic load dataset. The simulation demonstrates the balance on unlearning completeness and operational cost. All codes can be found at https://github.com/xuwkk/task_aware_machine_unlearning.

Availability Adversarial Attack and Countermeasures for Deep Learning-based Load Forecasting

The forecast of electrical loads is essential for the planning and operation of the power system. Recently, advances in deep learning have enabled more accurate forecasts. However, deep neural networks are prone to adversarial attacks. Although most of the literature focuses on integrity-based attacks, this paper proposes availability-based adversarial attacks, which can be more easily implemented by attackers. For each forecast instance, the availability attack position is optimally solved by mixed-integer reformulation of the artificial neural network. To tackle this attack, an adversarial training algorithm is proposed. In simulation, a realistic load forecasting dataset is considered and the attack performance is compared to the integrity-based attack. Meanwhile, the adversarial training algorithm is shown to significantly improve robustness against availability attacks. All codes are available at https://github.com/xuwkk/AAA_Load_Forecast.

Multi-Agent Reinforcement Learning for Active Voltage Control on Power Distribution Networks

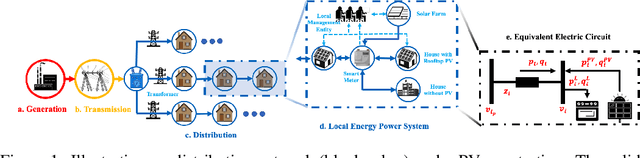
This paper presents a problem in power networks that creates an exciting and yet challenging real-world scenario for application of multi-agent reinforcement learning (MARL). The emerging trend of decarbonisation is placing excessive stress on power distribution networks. Active voltage control is seen as a promising solution to relieve power congestion and improve voltage quality without extra hardware investment, taking advantage of the controllable apparatuses in the network, such as roof-top photovoltaics (PVs) and static var compensators (SVCs). These controllable apparatuses appear in a vast number and are distributed in a wide geographic area, making MARL a natural candidate. This paper formulates the active voltage control problem in the framework of Dec-POMDP and establishes an open-source environment. It aims to bridge the gap between the power community and the MARL community and be a drive force towards real-world applications of MARL algorithms. Finally, we analyse the special characteristics of the active voltage control problems that cause challenges for state-of-the-art MARL approaches, and summarise the potential directions.