Efficient Model Compression Techniques with FishLeg

In many domains, the most successful AI models tend to be the largest, indeed often too large to be handled by AI players with limited computational resources. To mitigate this, a number of compression methods have been developed, including methods that prune the network down to high sparsity whilst retaining performance. The best-performing pruning techniques are often those that use second-order curvature information (such as an estimate of the Fisher information matrix) to score the importance of each weight and to predict the optimal compensation for weight deletion. However, these methods are difficult to scale to high-dimensional parameter spaces without making heavy approximations. Here, we propose the FishLeg surgeon (FLS), a new second-order pruning method based on the Fisher-Legendre (FishLeg) optimizer. At the heart of FishLeg is a meta-learning approach to amortising the action of the inverse FIM, which brings a number of advantages. Firstly, the parameterisation enables the use of flexible tensor factorisation techniques to improve computational and memory efficiency without sacrificing much accuracy, alleviating challenges associated with scalability of most second-order pruning methods. Secondly, directly estimating the inverse FIM leads to less sensitivity to the amplification of stochasticity during inversion, thereby resulting in more precise estimates. Thirdly, our approach also allows for progressive assimilation of the curvature into the parameterisation. In the gradual pruning regime, this results in a more efficient estimate refinement as opposed to re-estimation. We find that FishLeg achieves higher or comparable performance against two common baselines in the area, most notably in the high sparsity regime when considering a ResNet18 model on CIFAR-10 (84% accuracy at 95% sparsity vs 60% for OBS) and TinyIM (53% accuracy at 80% sparsity vs 48% for OBS).

Exact, Tractable Gauss-Newton Optimization in Deep Reversible Architectures Reveal Poor Generalization

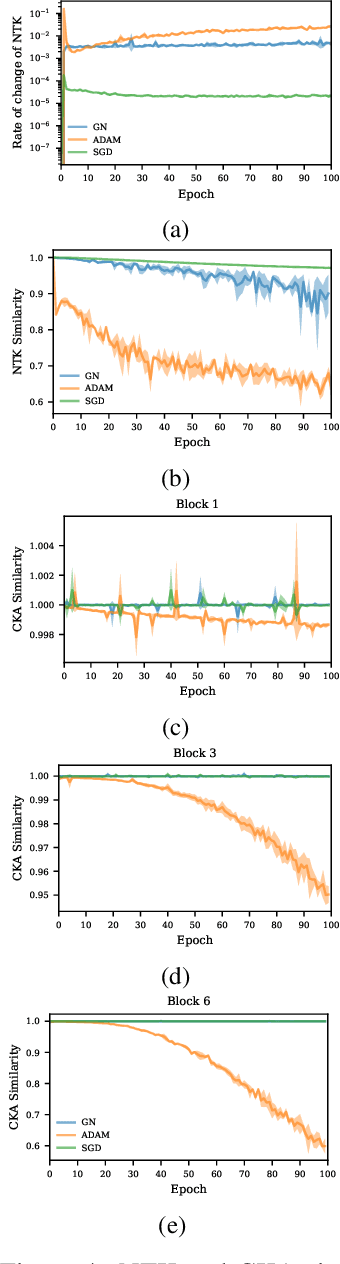
Second-order optimization has been shown to accelerate the training of deep neural networks in many applications, often yielding faster progress per iteration on the training loss compared to first-order optimizers. However, the generalization properties of second-order methods are still being debated. Theoretical investigations have proved difficult to carry out outside the tractable settings of heavily simplified model classes -- thus, the relevance of existing theories to practical deep learning applications remains unclear. Similarly, empirical studies in large-scale models and real datasets are significantly confounded by the necessity to approximate second-order updates in practice. It is often unclear whether the observed generalization behaviour arises specifically from the second-order nature of the parameter updates, or instead reflects the specific structured (e.g.\ Kronecker) approximations used or any damping-based interpolation towards first-order updates. Here, we show for the first time that exact Gauss-Newton (GN) updates take on a tractable form in a class of deep reversible architectures that are sufficiently expressive to be meaningfully applied to common benchmark datasets. We exploit this novel setting to study the training and generalization properties of the GN optimizer. We find that exact GN generalizes poorly. In the mini-batch training setting, this manifests as rapidly saturating progress even on the \emph{training} loss, with parameter updates found to overfit each mini-batchatch without producing the features that would support generalization to other mini-batches. We show that our experiments run in the ``lazy'' regime, in which the neural tangent kernel (NTK) changes very little during the course of training. This behaviour is associated with having no significant changes in neural representations, explaining the lack of generalization.

Natural continual learning: success is a journey, not (just) a destination

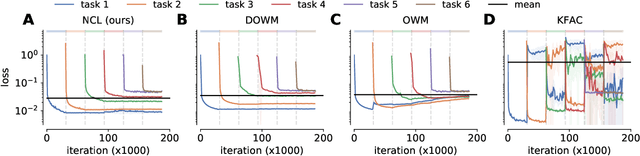
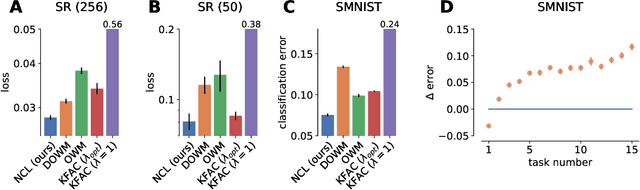
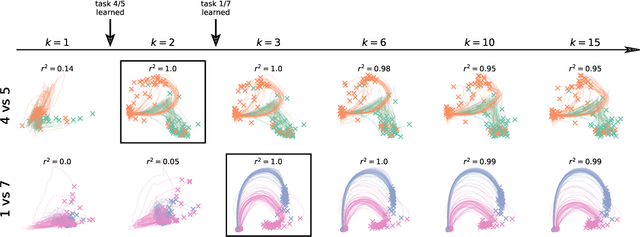
Biological agents are known to learn many different tasks over the course of their lives, and to be able to revisit previous tasks and behaviors with little to no loss in performance. In contrast, artificial agents are prone to 'catastrophic forgetting' whereby performance on previous tasks deteriorates rapidly as new ones are acquired. This shortcoming has recently been addressed using methods that encourage parameters to stay close to those used for previous tasks. This can be done by (i) using specific parameter regularizers that map out suitable destinations in parameter space, or (ii) guiding the optimization journey by projecting gradients into subspaces that do not interfere with previous tasks. However, parameter regularization has been shown to be relatively ineffective in recurrent neural networks (RNNs), a setting relevant to the study of neural dynamics supporting biological continual learning. Similarly, projection based methods can reach capacity and fail to learn any further as the number of tasks increases. To address these limitations, we propose Natural Continual Learning (NCL), a new method that unifies weight regularization and projected gradient descent. NCL uses Bayesian weight regularization to encourage good performance on all tasks at convergence and combines this with gradient projections designed to prevent catastrophic forgetting during optimization. NCL formalizes gradient projection as a trust region algorithm based on the Fisher information metric, and achieves scalability via a novel Kronecker-factored approximation strategy. Our method outperforms both standard weight regularization techniques and projection based approaches when applied to continual learning problems in RNNs. The trained networks evolve task-specific dynamics that are strongly preserved as new tasks are learned, similar to experimental findings in biological circuits.

Automatic differentiation of Sylvester, Lyapunov, and algebraic Riccati equations

Sylvester, Lyapunov, and algebraic Riccati equations are the bread and butter of control theorists. They are used to compute infinite-horizon Gramians, solve optimal control problems in continuous or discrete time, and design observers. While popular numerical computing frameworks (e.g., scipy) provide efficient solvers for these equations, these solvers are still largely missing from most automatic differentiation libraries. Here, we derive the forward and reverse-mode derivatives of the solutions to all three types of equations, and showcase their application on an inverse control problem.

Manifold GPLVMs for discovering non-Euclidean latent structure in neural data

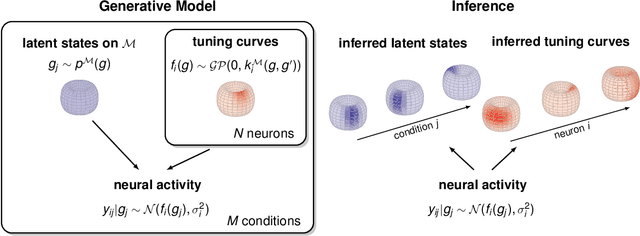
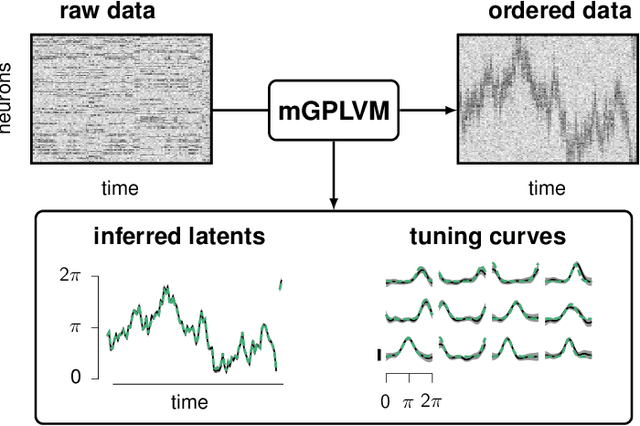
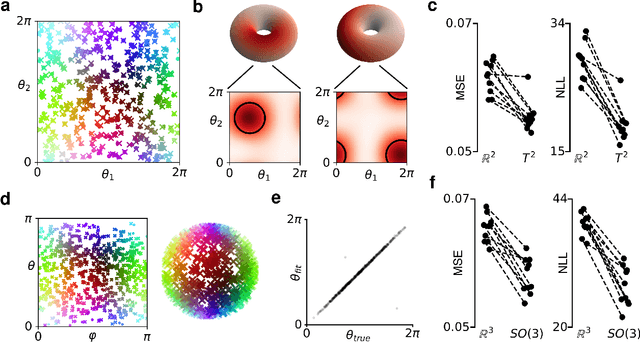
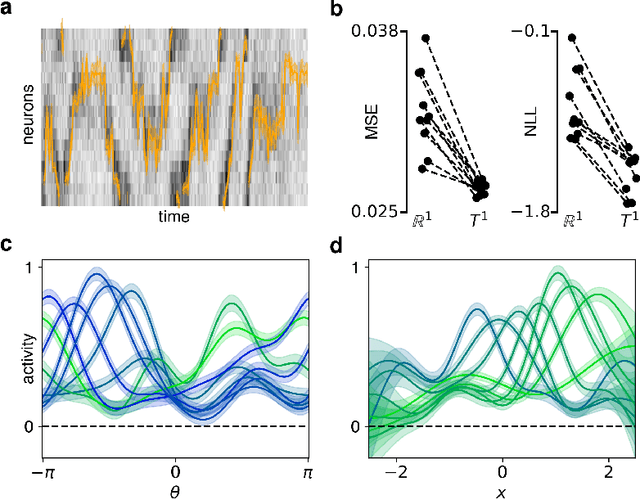
A common problem in neuroscience is to elucidate the collective neural representations of behaviorally important variables such as head direction, spatial location, upcoming movements, or mental spatial transformations. Often, these latent variables are internal constructs not directly accessible to the experimenter. Here, we propose a new probabilistic latent variable model to simultaneously identify the latent state and the way each neuron contributes to its representation in an unsupervised way. In contrast to previous models which assume Euclidean latent spaces, we embrace the fact that latent states often belong to symmetric manifolds such as spheres, tori, or rotation groups of various dimensions. We therefore propose the manifold Gaussian process latent variable model (mGPLVM), where neural responses arise from (i) a shared latent variable living on a specific manifold, and (ii) a set of non-parametric tuning curves determining how each neuron contributes to the representation. Cross-validated comparisons of models with different topologies can be used to distinguish between candidate manifolds, and variational inference enables quantification of uncertainty. We demonstrate the validity of the approach on several synthetic datasets and on calcium recordings from the ellipsoid body of Drosophila melanogaster. This circuit is known to encode head direction, and mGPLVM correctly recovers the ring topology expected from a neural population representing a single angular variable.