Kristopher T. Jensen
An introduction to reinforcement learning for neuroscience
Nov 13, 2023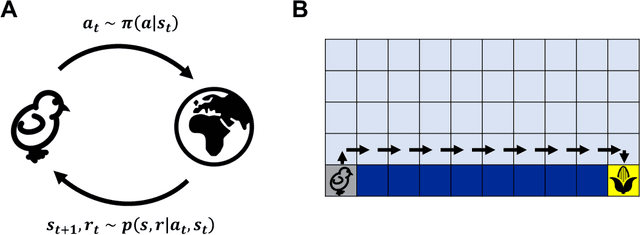
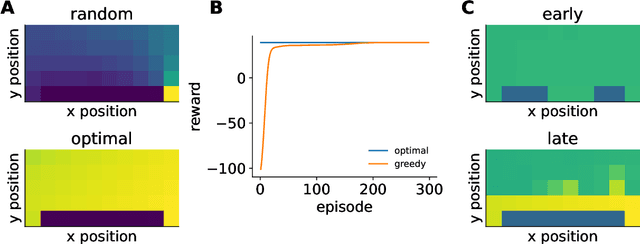
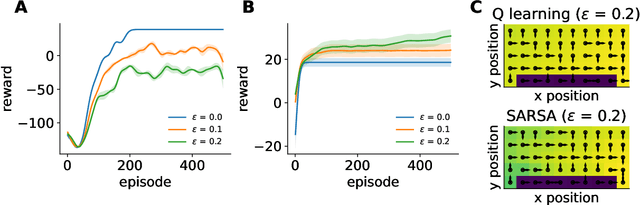
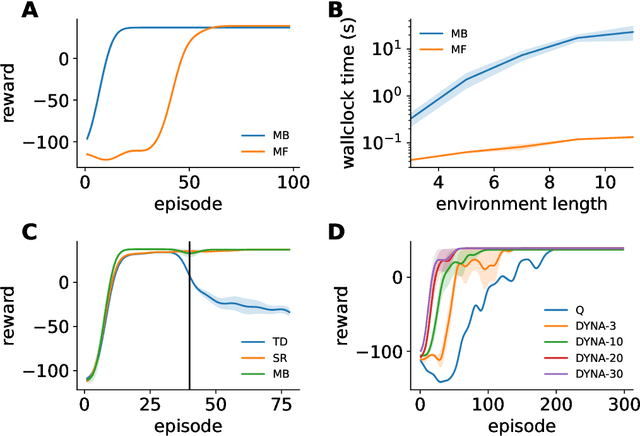
Abstract:Reinforcement learning has a rich history in neuroscience, from early work on dopamine as a reward prediction error signal for temporal difference learning (Schultz et al., 1997) to recent work suggesting that dopamine could implement a form of 'distributional reinforcement learning' popularized in deep learning (Dabney et al., 2020). Throughout this literature, there has been a tight link between theoretical advances in reinforcement learning and neuroscientific experiments and findings. As a result, the theories describing our experimental data have become increasingly complex and difficult to navigate. In this review, we cover the basic theory underlying classical work in reinforcement learning and build up to an introductory overview of methods used in modern deep reinforcement learning that have found applications in systems neuroscience. We start with an overview of the reinforcement learning problem and classical temporal difference algorithms, followed by a discussion of 'model-free' and 'model-based' reinforcement learning together with methods such as DYNA and successor representations that fall in between these two categories. Throughout these sections, we highlight the close parallels between the machine learning methods and related work in both experimental and theoretical neuroscience. We then provide an introduction to deep reinforcement learning with examples of how these methods have been used to model different learning phenomena in the systems neuroscience literature, such as meta-reinforcement learning (Wang et al., 2018) and distributional reinforcement learning (Dabney et al., 2020). Code that implements the methods discussed in this work and generates the figures is also provided.
Understanding Neural Coding on Latent Manifolds by Sharing Features and Dividing Ensembles
Oct 06, 2022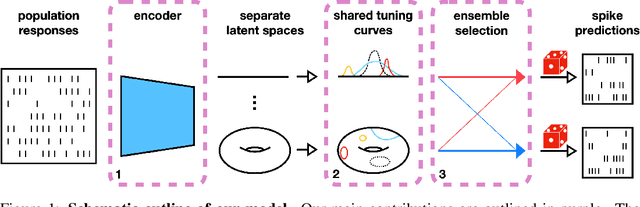
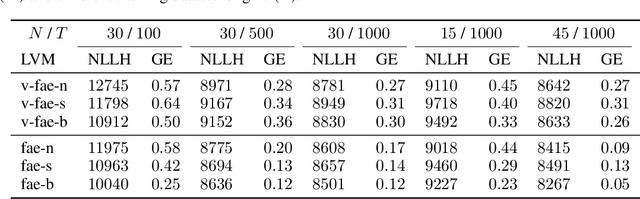
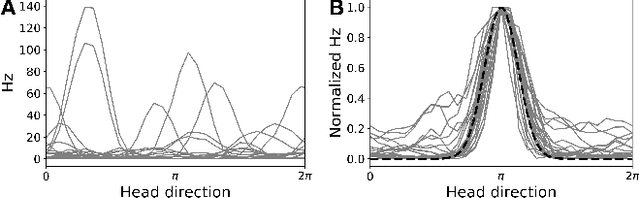
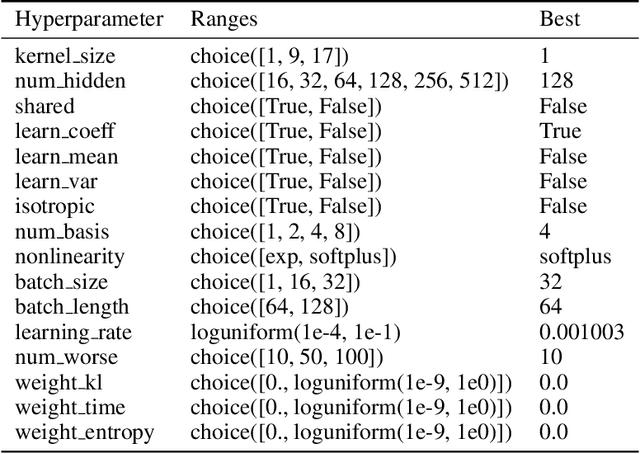
Abstract:Systems neuroscience relies on two complementary views of neural data, characterized by single neuron tuning curves and analysis of population activity. These two perspectives combine elegantly in neural latent variable models that constrain the relationship between latent variables and neural activity, modeled by simple tuning curve functions. This has recently been demonstrated using Gaussian processes, with applications to realistic and topologically relevant latent manifolds. Those and previous models, however, missed crucial shared coding properties of neural populations. We propose feature sharing across neural tuning curves, which significantly improves performance and leads to better-behaved optimization. We also propose a solution to the problem of ensemble detection, whereby different groups of neurons, i.e., ensembles, can be modulated by different latent manifolds. This is achieved through a soft clustering of neurons during training, thus allowing for the separation of mixed neural populations in an unsupervised manner. These innovations lead to more interpretable models of neural population activity that train well and perform better even on mixtures of complex latent manifolds. Finally, we apply our method on a recently published grid cell dataset, recovering distinct ensembles, inferring toroidal latents and predicting neural tuning curves all in a single integrated modeling framework.
Natural continual learning: success is a journey, not (just) a destination
Jun 15, 2021
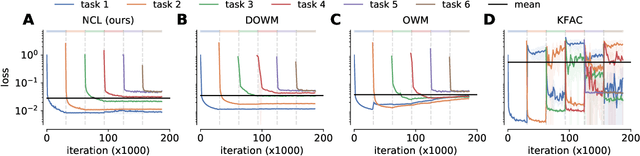
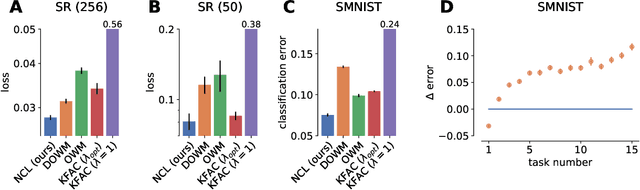
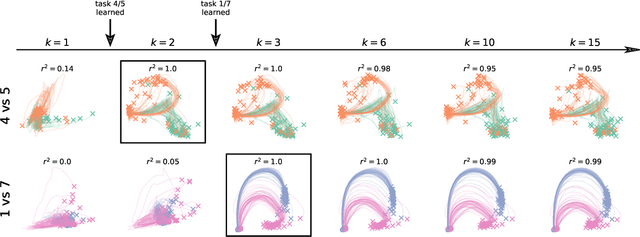
Abstract:Biological agents are known to learn many different tasks over the course of their lives, and to be able to revisit previous tasks and behaviors with little to no loss in performance. In contrast, artificial agents are prone to 'catastrophic forgetting' whereby performance on previous tasks deteriorates rapidly as new ones are acquired. This shortcoming has recently been addressed using methods that encourage parameters to stay close to those used for previous tasks. This can be done by (i) using specific parameter regularizers that map out suitable destinations in parameter space, or (ii) guiding the optimization journey by projecting gradients into subspaces that do not interfere with previous tasks. However, parameter regularization has been shown to be relatively ineffective in recurrent neural networks (RNNs), a setting relevant to the study of neural dynamics supporting biological continual learning. Similarly, projection based methods can reach capacity and fail to learn any further as the number of tasks increases. To address these limitations, we propose Natural Continual Learning (NCL), a new method that unifies weight regularization and projected gradient descent. NCL uses Bayesian weight regularization to encourage good performance on all tasks at convergence and combines this with gradient projections designed to prevent catastrophic forgetting during optimization. NCL formalizes gradient projection as a trust region algorithm based on the Fisher information metric, and achieves scalability via a novel Kronecker-factored approximation strategy. Our method outperforms both standard weight regularization techniques and projection based approaches when applied to continual learning problems in RNNs. The trained networks evolve task-specific dynamics that are strongly preserved as new tasks are learned, similar to experimental findings in biological circuits.
Manifold GPLVMs for discovering non-Euclidean latent structure in neural data
Jun 12, 2020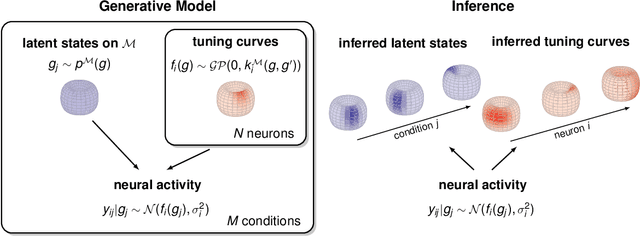
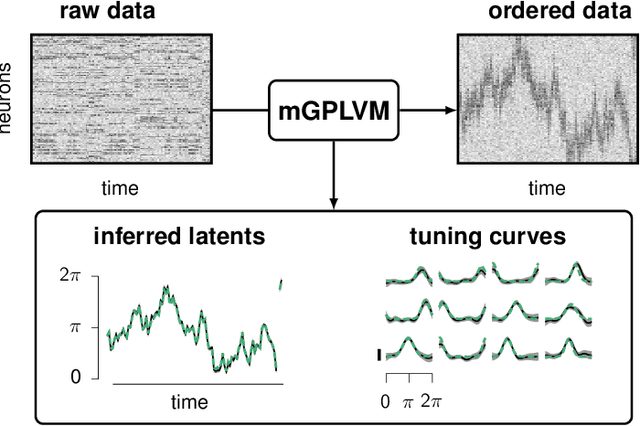
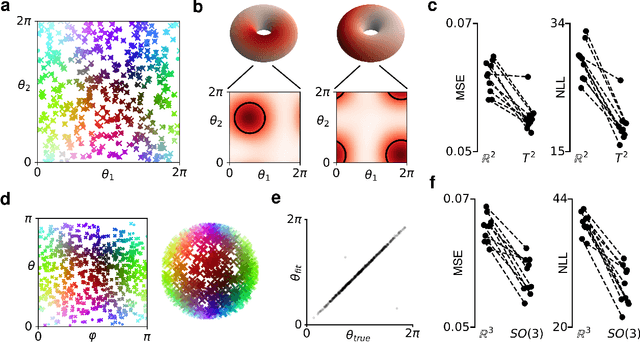
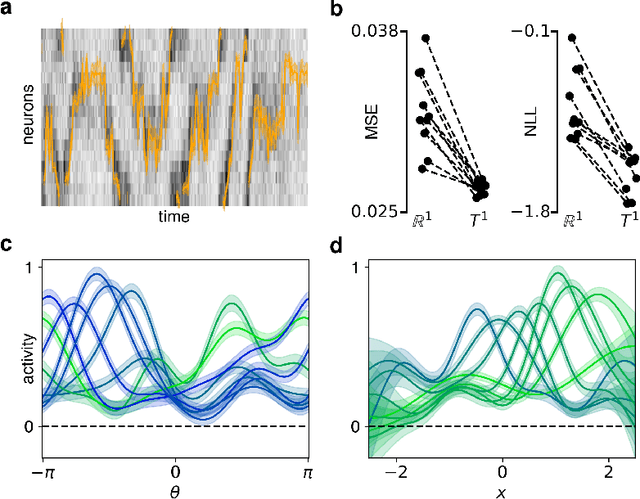
Abstract:A common problem in neuroscience is to elucidate the collective neural representations of behaviorally important variables such as head direction, spatial location, upcoming movements, or mental spatial transformations. Often, these latent variables are internal constructs not directly accessible to the experimenter. Here, we propose a new probabilistic latent variable model to simultaneously identify the latent state and the way each neuron contributes to its representation in an unsupervised way. In contrast to previous models which assume Euclidean latent spaces, we embrace the fact that latent states often belong to symmetric manifolds such as spheres, tori, or rotation groups of various dimensions. We therefore propose the manifold Gaussian process latent variable model (mGPLVM), where neural responses arise from (i) a shared latent variable living on a specific manifold, and (ii) a set of non-parametric tuning curves determining how each neuron contributes to the representation. Cross-validated comparisons of models with different topologies can be used to distinguish between candidate manifolds, and variational inference enables quantification of uncertainty. We demonstrate the validity of the approach on several synthetic datasets and on calcium recordings from the ellipsoid body of Drosophila melanogaster. This circuit is known to encode head direction, and mGPLVM correctly recovers the ring topology expected from a neural population representing a single angular variable.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge